Урок разработан учителем математики МБОУ «СОШ №34», г. Бийска Алтайского края Масловой Светланой Константиновной,
при участии учащихся 10 класса (Пановой В, Галкиной А, Ралдугина И, Хисамутдинова А)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для 10 класса Числовые функции
Содержание
- 1. Презентация по математике для 10 класса Числовые функции
- 2. «Определение числовой функции и способы её задания»Учащийся 10 класса Хисамутдинов А
- 3. Определение 1Если даны числовое множество Х и
- 4. Способы задания функции. Аналитический. Графический. Табличный.Учащийся 10 класса Хисамутдинов А
- 5. Определение 2Если дана функция у = f
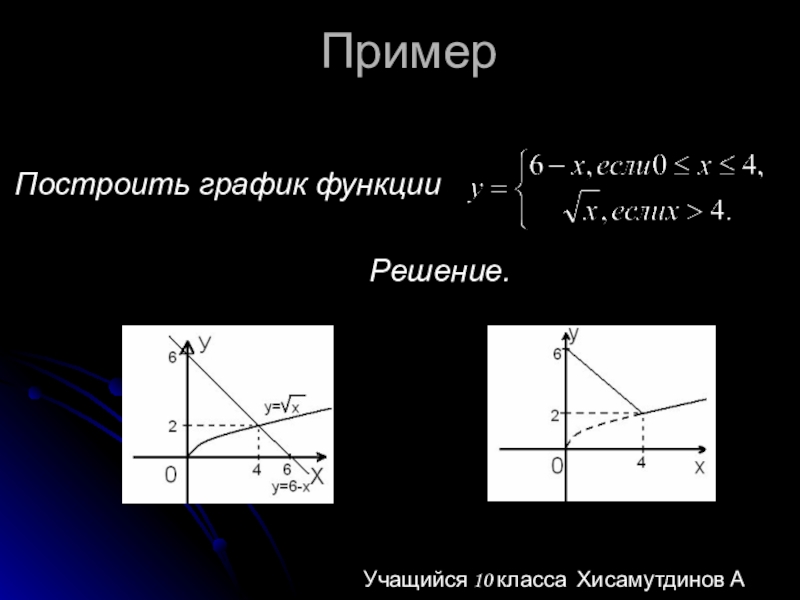
- 6. Пример Построить график функции
- 7. №1. Выясните,
- 8. №2. Найдите область определения
- 9. Свойства функций:Область определения функции D(f)Область значений функции
- 10. Пример Построить график кусочной функции и
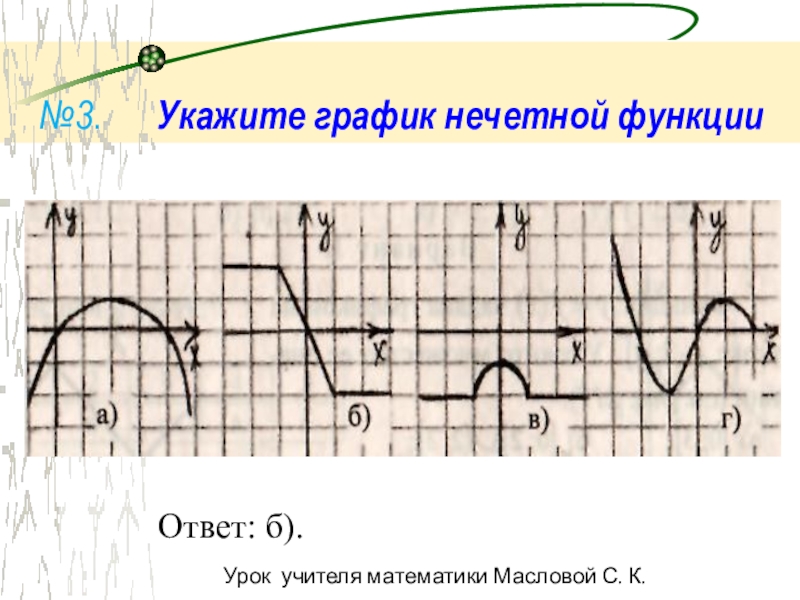
- 11. Ответ: б). №3. Укажите график нечетной функцииУрок учителя математики Масловой С. К.
- 12. Периодические функции.Функцию, имеющую отличный
- 13. Слайд 13
- 14. №4. Постройте график периодической
- 15. Обратная функцияОПРЕДЕЛЕНИЕ ФУНКЦИЮ Y=F(X),XЄX НАЗЫВАЮТ ОБРАТИМОЙ
- 16. Определения Пусть обратимая функцияY=F(X)Определена на множестве X
- 17. Tеорема 1 Если функция y=f(x) монотонна на
- 18. Пример Показать ,что для функции y=5x-3
- 19. №5. Для функции, заданной
- 20. №6. у = f(x) и
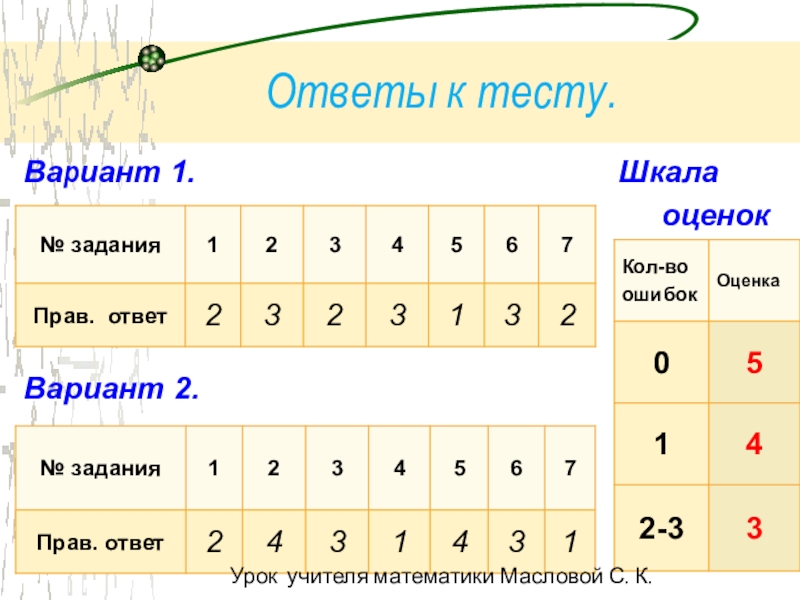
- 21. Ответы к тесту. Вариант
- 22. Домашнее задание.Учебник 10 класса Алгебра и начала
Слайд 1
Числовые
функции
Установить соответствие
Слайд 3Определение 1
Если даны числовое множество Х и правило f, позволяющее поставить
Множество всех значений функций у = f (x), х є Х называют областью значений функции и обозначают E (f).
Учащийся 10 класса Хисамутдинов А
Слайд 4Способы задания функции.
Аналитический.
Графический.
Табличный.
Учащийся 10 класса Хисамутдинов А
Слайд 5Определение 2
Если дана функция у = f (x), x принадлежит Х
Учащийся 10 класса Хисамутдинов А
Слайд 7 №1. Выясните, на каком рисунке указаны
Ответ: a) D(f)=(-3;3], E(f)=(-1;3], в) D(f)=[-1; +∞), E(f)=[-2; +∞).
Урок учителя математики Масловой С. К.
Слайд 8№2. Найдите область определения функций
Ответ: [-12;-1)U(-1;1) U(1; +∞)
Урок учителя математики Масловой С. К.
Слайд 9Свойства функций:
Область определения функции D(f)
Область значений функции Е(f)
Нули функции
Промежутки знакопостоянства
Промежутки монотонности
Наибольшее
Четность (нечетность) функции
Точки экстремумов – max и min
Периодичность функции
Ограниченность функции
Промежутки непрерывности
Выпуклость функции
Асимптоты
Учащаяся 10 класса Панова В
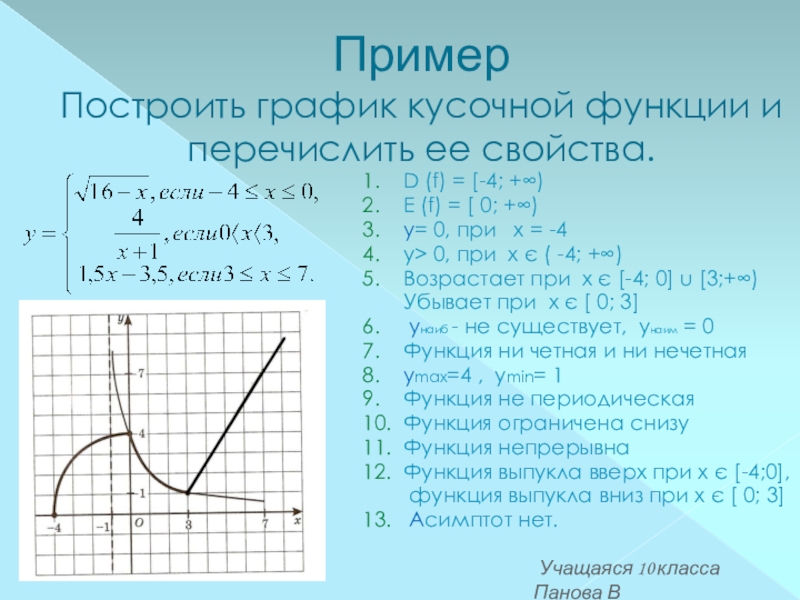
Слайд 10Пример
Построить график кусочной функции и перечислить ее свойства.
1. D
2. E (f) = [ 0; +∞)
3. у= 0, при х = -4
4. у> 0, при х є ( -4; +∞)
5. Возрастает при х є [-4; 0] u [3;+∞)
Убывает при х є [ 0; 3]
6. унаиб - не существует, унаим = 0
7. Функция ни четная и ни нечетная
8. уmax=4 , уmin= 1
9. Функция не периодическая
10. Функция ограничена снизу
11. Функция непрерывна
12. Функция выпукла вверх при х є [-4;0],
функция выпукла вниз при х є [ 0; 3]
13. Асимптот нет.
Учащаяся 10 класса Панова В
Слайд 12 Периодические функции.
Функцию, имеющую отличный от нуля период Т,
Если функция у = f(х), х∈Х имеет период Т, то любое число, кратное Т(т.е. число вида kТ, kєZ), также является её периодом.
выполняются равенства:
f(х - Т) = f(х) = f(х + Т)
Учащаяся 10 класса Галкина А
Слайд 13 Пример.
Доказать, что функция у
Решение.
Числа х и х ± k, где k – любое целое число, имеет одинаковую дробную часть, т. е. {х - k} = {х} = {х + k}. Значит, любое целое число является периодом функции;
есть и основной период: Т = 1.
Учащаяся 10 класса Галкина А
Слайд 14№4. Постройте график периодической функции f(x)=ІxІ с
Урок учителя математики Масловой С. К.
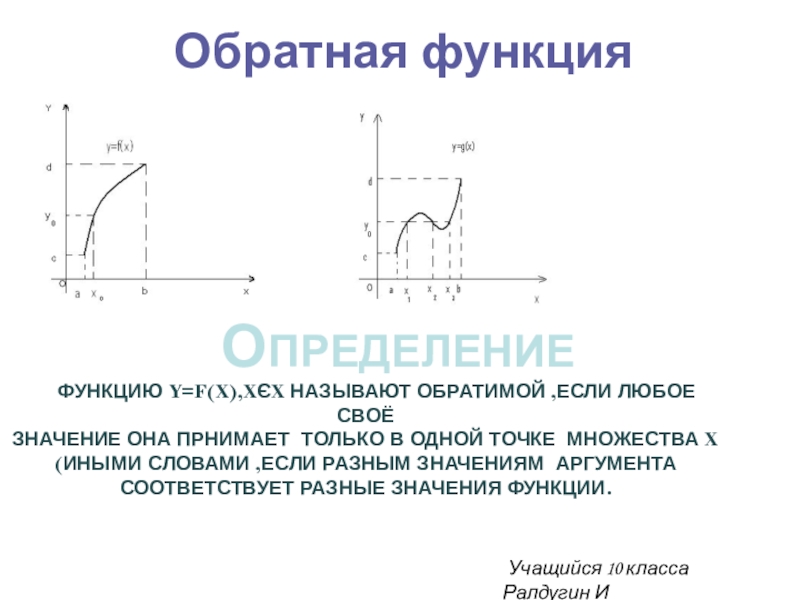
Слайд 15Обратная функция
ОПРЕДЕЛЕНИЕ
ФУНКЦИЮ Y=F(X),XЄX НАЗЫВАЮТ ОБРАТИМОЙ ,ЕСЛИ ЛЮБОЕ СВОЁ
ЗНАЧЕНИЕ ОНА
(ИНЫМИ СЛОВАМИ ,ЕСЛИ РАЗНЫМ ЗНАЧЕНИЯМ АРГУМЕНТА
СООТВЕТСТВУЕТ РАЗНЫЕ ЗНАЧЕНИЯ ФУНКЦИИ.
Учащийся 10 класса Ралдугин И
Слайд 16Определения
Пусть обратимая функцияY=F(X)Определена на множестве X и E(f)=Y.Поставим в соответствие
Тогда получим функцию , которая определена Y,а X-область значений функций . Эту функцию обозначают x=f-1 (y) и называют обратной по отношению к функции y=f(x).
Учащийся 10 класса Ралдугин И
Слайд 17Tеорема 1
Если функция y=f(x) монотонна на множестве X, то она
Теорема 2
Если функция y=f(x) возрастает
(убывает) на множестве x, а Y –область
Значений функции, то обратная функция
X=f-1(y) возрастает (убывает) наY.
Учащийся 10 класса Ралдугин И
Слайд 18
Пример
Показать ,что для функции y=5x-3 существует обратная функция ,и найти её
Решение.
Линейная функция Y=5X-3 определена на R,возрастает на R и область её значений есть R. Значит , обратная функция существует на R. Чтобы найти её аналитическое выражение ,решим уравнение Y=5X-3 относительно x; получим:X=(y+3)/5.Это и есть искомая обратная функция. Она определена и возрастает на R.
Учащийся 10 класса Ралдугин И
Слайд 19№5. Для функции, заданной табличным способом, укажите её
а) б)
Ответ: а) нет, б) да.
Урок учителя математики Масловой С. К.
Слайд 20№6. у = f(x) и y = g(x) –
Ответ: 1/3, -3.
Урок учителя математики Масловой С. К.
Слайд 22Домашнее задание.
Учебник 10 класса Алгебра и начала анализа (в 2-х частях)
9.28, 10.27 (в), 8.32 (б).
Урок учителя математики Масловой С. К.