- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике 9 класс Квадратичная функция
Содержание
- 1. Презентация по математике 9 класс Квадратичная функция
- 2. Цели урока:1. Изучить свойства квадратичной функции.2. Закрепить
- 3. Из предложенных функций выберите квадратичную функцию
- 4. Назовите те параболы, ветви которых будут
- 5. Алгоритм исследования функции1. Область определения функции –
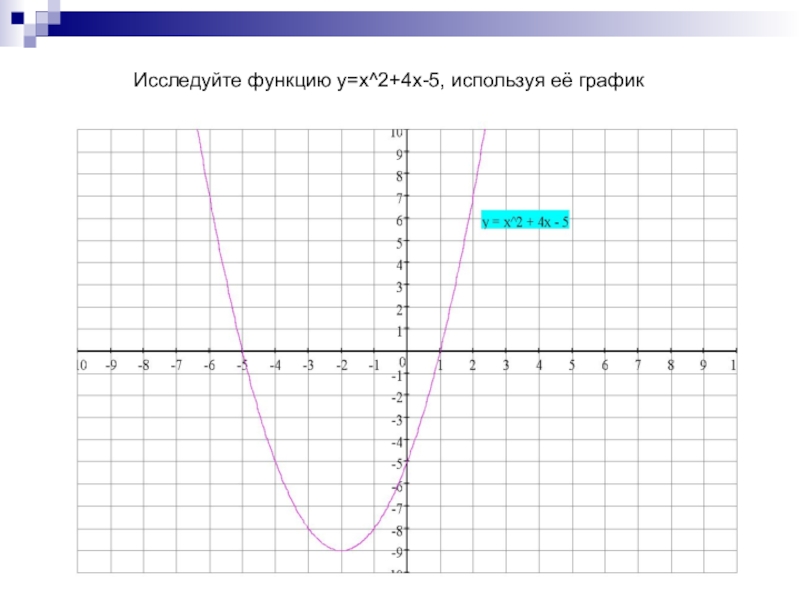
- 6. Исследуйте функцию у=x^2+4x-5, используя её график
- 7. Свойства графикаD(y) = (-∞; +∞)E(y) = (-9;
- 8. 123456 Назовите число корней уравнения
- 9. Построить график функции y= х2 – x
- 10. Y=x2 – x -6
- 11. Ответьте на вопросы:Назовите координаты вершины параболы;Назовите ось
- 12. Задание: Построить график функции :
- 13. Построим график , используя свойства квадратичной функции
- 14. Ось симметрииD(y) = (- ∞; +∞)E(y) =
Цели урока:1. Изучить свойства квадратичной функции.2. Закрепить их знание при построении графиков квадратичной функции.3. Уметь определять свойства функции по графику.
Слайд 1
Квадратичная функция, ее график и свойства
Учитель математики
МОУ Кузнечихинская СШ ЯМР
Уваева Е.А.
Слайд 2Цели урока:
1. Изучить свойства квадратичной функции.
2. Закрепить их знание при построении
графиков квадратичной функции.
3. Уметь определять свойства функции по графику.
3. Уметь определять свойства функции по графику.
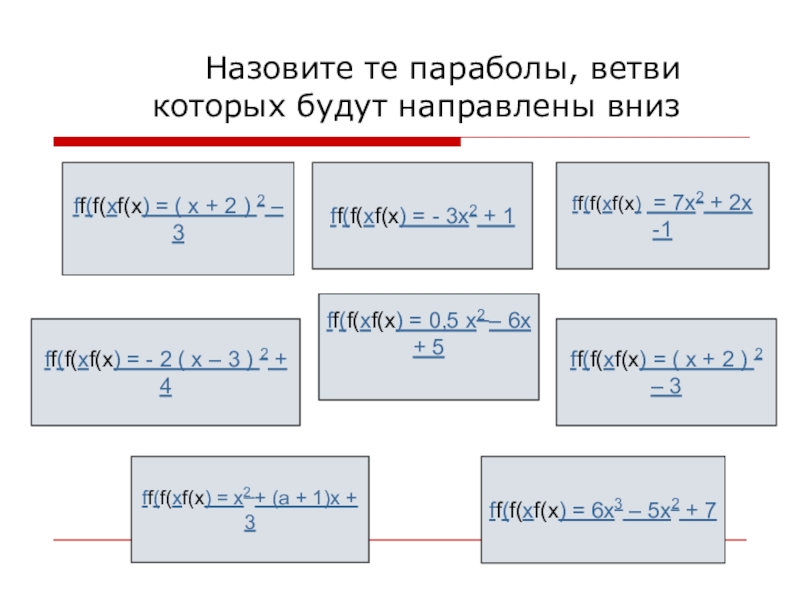
Слайд 4 Назовите те параболы, ветви которых будут направлены вниз
ff(f(xf(x) = -
2 ( х – 3 ) 2 + 4
ff(f(xf(x) = 7х2 + 2х -1
ff(f(xf(x) = ( х + 2 ) 2 – 3
ff(f(xf(x) = х2 + (а + 1)х + 3
ff(f(xf(x) = 0,5 х2 – 6х + 5
ff(f(xf(x) = 6х3 – 5х2 + 7
ff(f(xf(x) = ( х + 2 ) 2 – 3
ff(f(xf(x) = - 3х2 + 1
Слайд 5Алгоритм исследования функции
1. Область определения функции – D(y)
-
все значения, которые может принимать аргумент
2. Область значения функции – E(y)
- все значения, которые может принимать функция
3. Координаты точек пересечения с осями координат
4. Промежутки знакопостоянства
- промежутки, на которых значения функции положительны, отрицательны
5. Промежутки возрастания, убывания функции
Функция возрастает (убывает) на промежутке, если большему значению аргумента соответствует большее (меньшее) значение функции
6 Наибольшее, наименьшее значение функции
2. Область значения функции – E(y)
- все значения, которые может принимать функция
3. Координаты точек пересечения с осями координат
4. Промежутки знакопостоянства
- промежутки, на которых значения функции положительны, отрицательны
5. Промежутки возрастания, убывания функции
Функция возрастает (убывает) на промежутке, если большему значению аргумента соответствует большее (меньшее) значение функции
6 Наибольшее, наименьшее значение функции
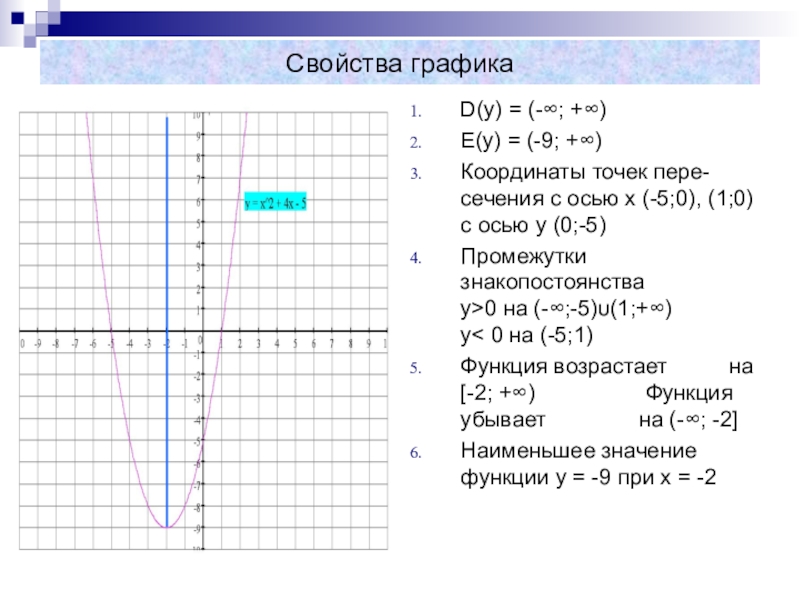
Слайд 7Свойства графика
D(y) = (-∞; +∞)
E(y) = (-9; +∞)
Координаты точек пере- сечения
с осью x (-5;0), (1;0) с осью у (0;-5)
Промежутки знакопостоянства у>0 на (-∞;-5)υ(1;+∞) у< 0 на (-5;1)
Функция возрастает на [-2; +∞) Функция убывает на (-∞; -2]
Наименьшее значение функции у = -9 при х = -2
Промежутки знакопостоянства у>0 на (-∞;-5)υ(1;+∞) у< 0 на (-5;1)
Функция возрастает на [-2; +∞) Функция убывает на (-∞; -2]
Наименьшее значение функции у = -9 при х = -2
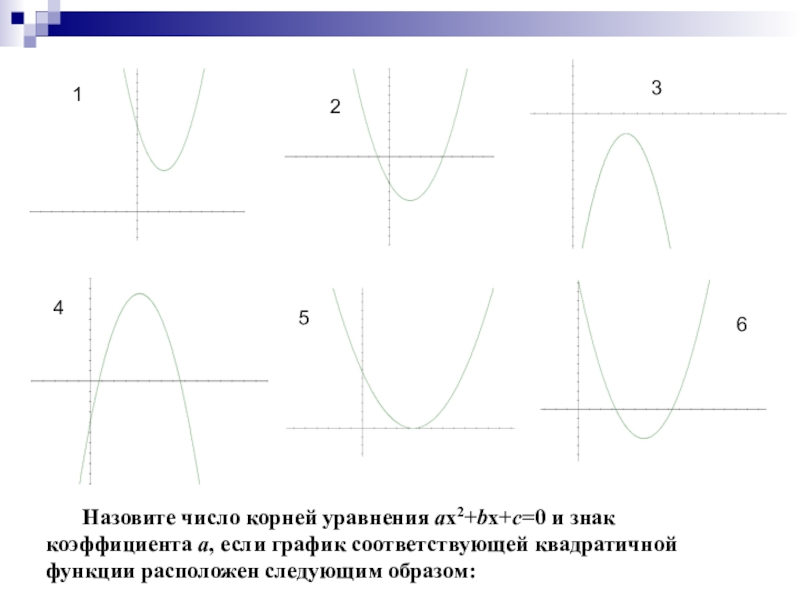
Слайд 81
2
3
4
5
6
Назовите число корней уравнения ax2+bx+c=0 и знак коэффициента
а, если график соответствующей квадратичной функции расположен следующим образом:
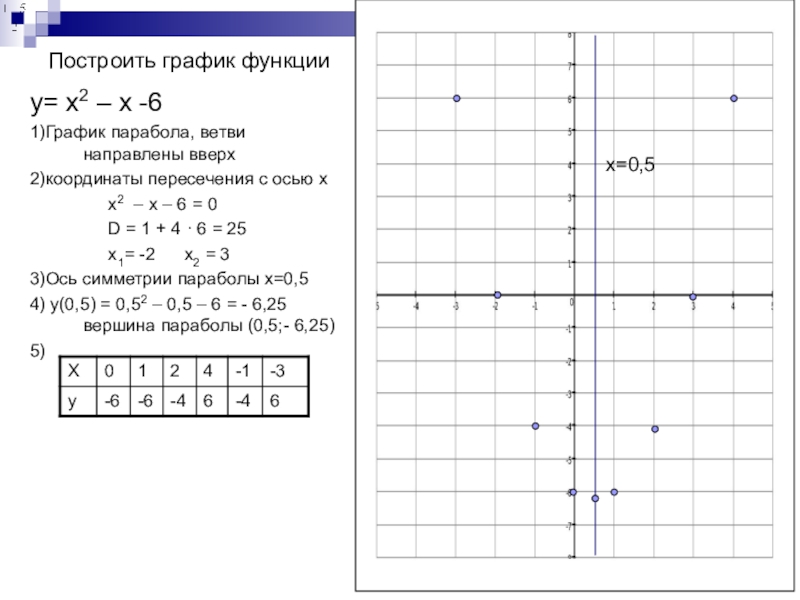
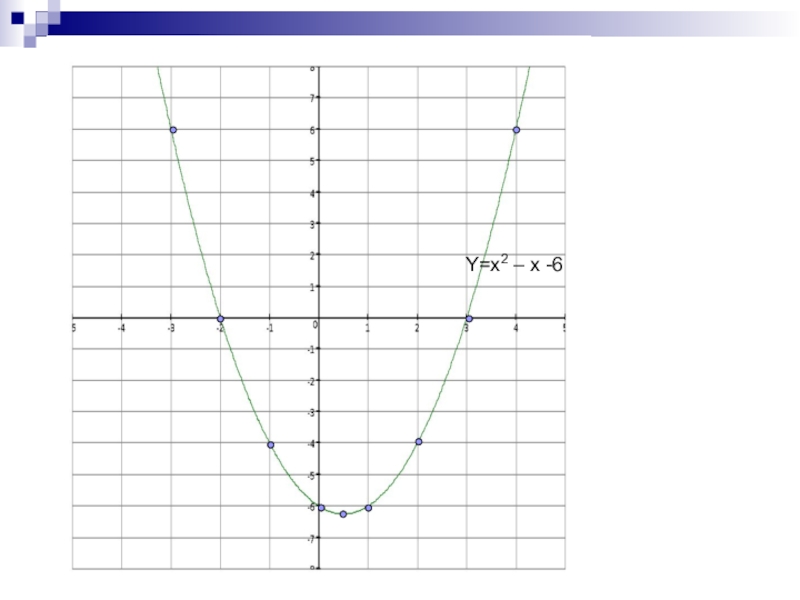
Слайд 9Построить график функции
y= х2 – x -6
1)График парабола, ветви направлены
вверх
2)координаты пересечения с осью х
x2 – x – 6 = 0
D = 1 + 4 · 6 = 25
x1= -2 x2 = 3
3)Ось симметрии параболы x=0,5
4) у(0,5) = 0,52 – 0,5 – 6 = - 6,25 вершина параболы (0,5;- 6,25)
5)
2)координаты пересечения с осью х
x2 – x – 6 = 0
D = 1 + 4 · 6 = 25
x1= -2 x2 = 3
3)Ось симметрии параболы x=0,5
4) у(0,5) = 0,52 – 0,5 – 6 = - 6,25 вершина параболы (0,5;- 6,25)
5)
x=0,5
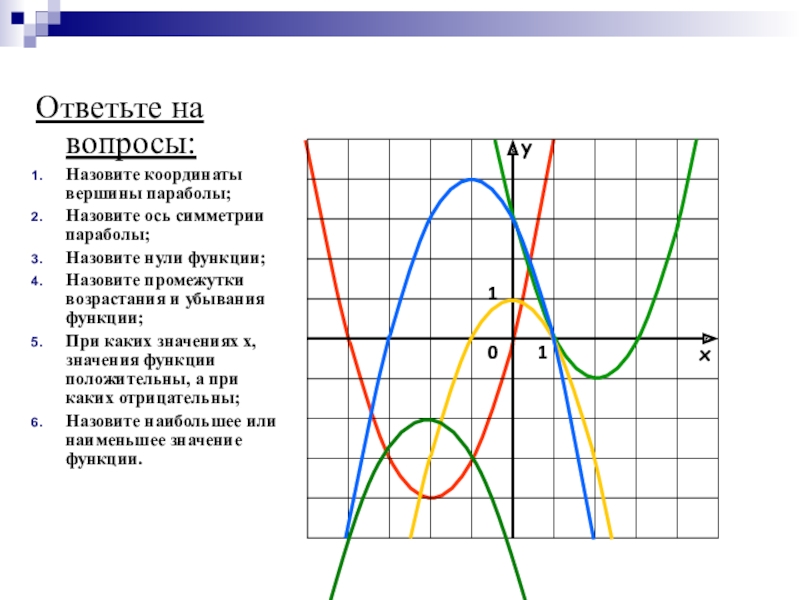
Слайд 11Ответьте на вопросы:
Назовите координаты вершины параболы;
Назовите ось симметрии параболы;
Назовите нули функции;
Назовите
промежутки возрастания и убывания функции;
При каких значениях х, значения функции положительны, а при каких отрицательны;
Назовите наибольшее или наименьшее значение функции.
При каких значениях х, значения функции положительны, а при каких отрицательны;
Назовите наибольшее или наименьшее значение функции.
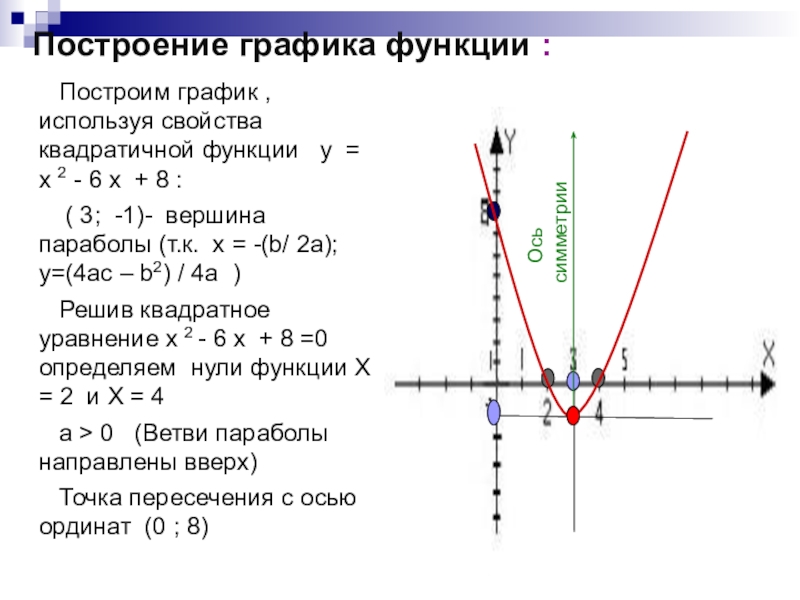
Слайд 13Построим график , используя свойства квадратичной функции у = х
2 - 6 х + 8 :
( 3; -1)- вершина параболы (т.к. х = -(b/ 2a); y=(4ac – b2) / 4a )
Решив квадратное уравнение х 2 - 6 х + 8 =0 определяем нули функции Х = 2 и Х = 4
а > 0 (Ветви параболы направлены вверх)
Точка пересечения с осью ординат (0 ; 8)
( 3; -1)- вершина параболы (т.к. х = -(b/ 2a); y=(4ac – b2) / 4a )
Решив квадратное уравнение х 2 - 6 х + 8 =0 определяем нули функции Х = 2 и Х = 4
а > 0 (Ветви параболы направлены вверх)
Точка пересечения с осью ординат (0 ; 8)
Построение графика функции :
Ось симметрии
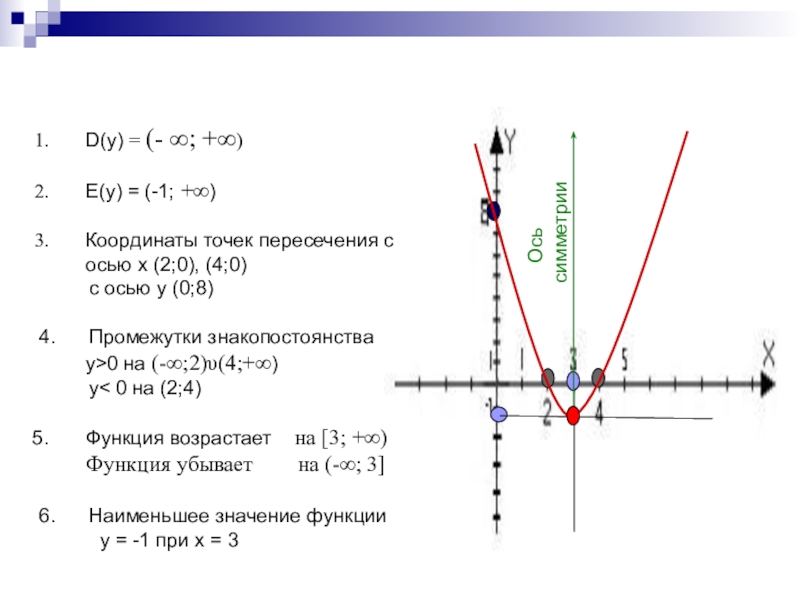
Слайд 14
Ось симметрии
D(y) = (- ∞; +∞)
E(y) = (-1; +∞)
Координаты точек пересечения
с осью x (2;0), (4;0)
с осью у (0;8)
4. Промежутки знакопостоянства у>0 на (-∞;2)υ(4;+∞)
у< 0 на (2;4)
Функция возрастает на [3; +∞) Функция убывает на (-∞; 3]
6. Наименьшее значение функции
у = -1 при х = 3
с осью у (0;8)
4. Промежутки знакопостоянства у>0 на (-∞;2)υ(4;+∞)
у< 0 на (2;4)
Функция возрастает на [3; +∞) Функция убывает на (-∞; 3]
6. Наименьшее значение функции
у = -1 при х = 3