- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике 10 класс на тему Простейшие тригонометрические уравнения
Содержание
- 1. Презентация по математике 10 класс на тему Простейшие тригонометрические уравнения
- 2. arcsin (-a)= - arcsin aarccos (-a)= π
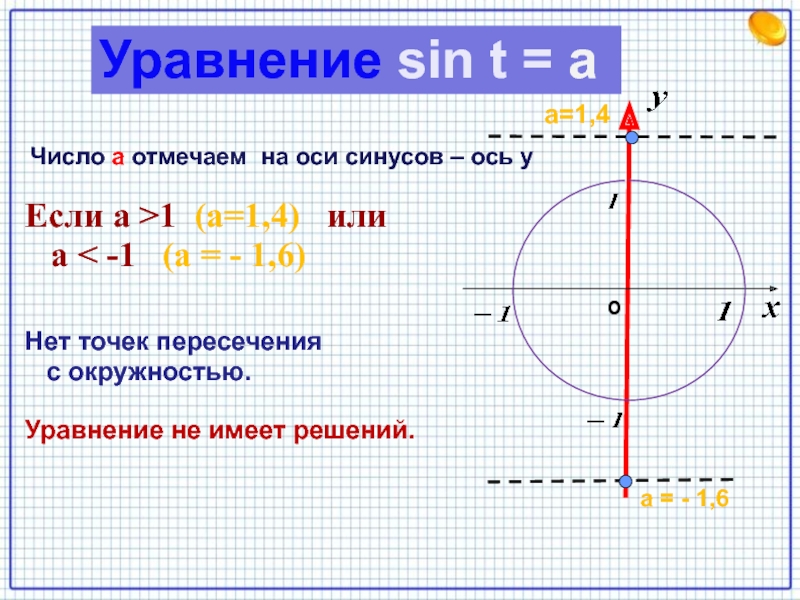
- 3. Если а >1 (а=1,4) или
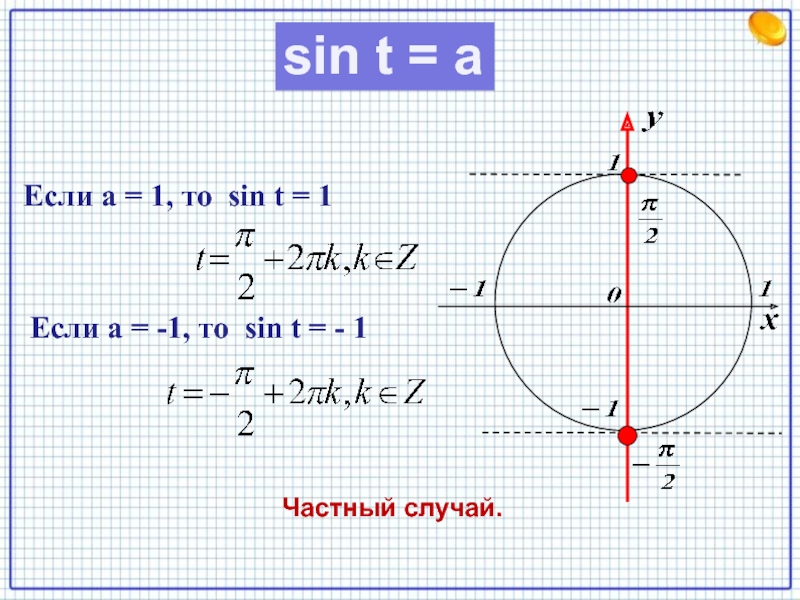
- 4. Если а = 1, то sin t
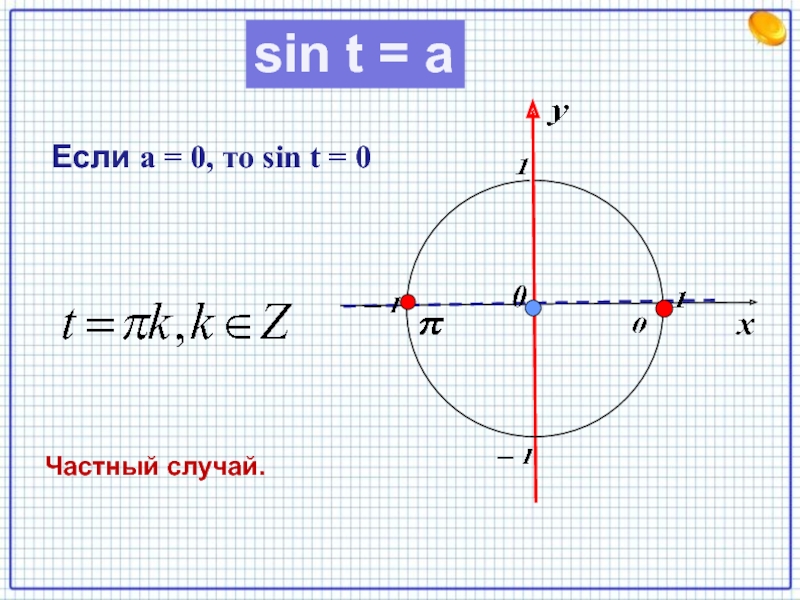
- 5. Если а = 0, то sin t = 0Частный случай.sin t = a
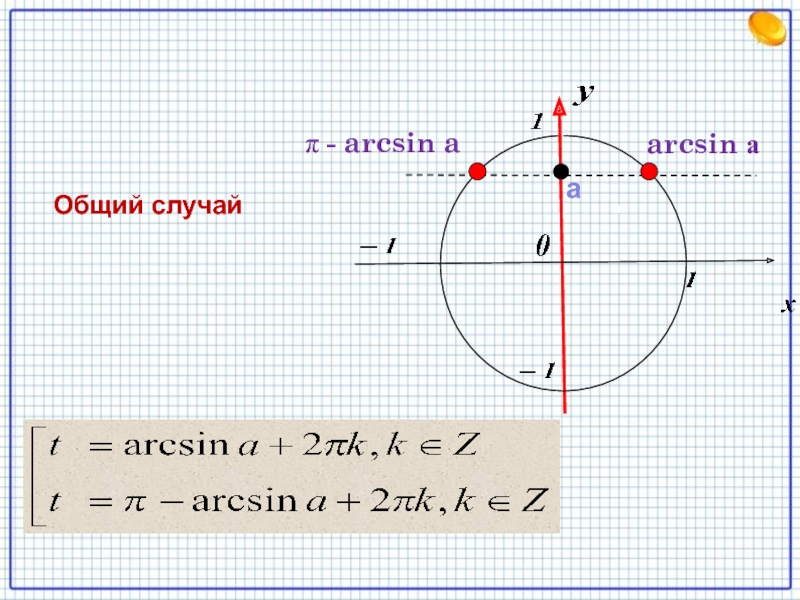
- 6. Общий случайarcsin ааπ - arcsin aа Если -1< а
- 7. Решение уравнения sin t = aОбщий случай:
- 8. Слайд 8
- 9. Характерная ошибкаУчащиеся делят обе части на 4 и получают следующее:Грубая ошибка.
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. arcsin (-a)= - arcsin a
- 14. Слайд 14
- 15. Приводим уравнение к стандартному виду:sin t = a
- 16. Слайд 16
- 17. Потренируйся
- 18. Если а >1 (а=1,4) или
- 19. cos t = aЧастный случай.Если а =
- 20. cos t = a Если а = 0, то сos t = 0Частный случай.
- 21. arccos а-arccos ааЕсли -1< а
- 22. Решение уравнения cos t = aОбщий случай: -1< а
- 23. Слайд 23
- 24. Слайд 24
- 25. arccos (-a)= π - arccos a
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Потренируйся
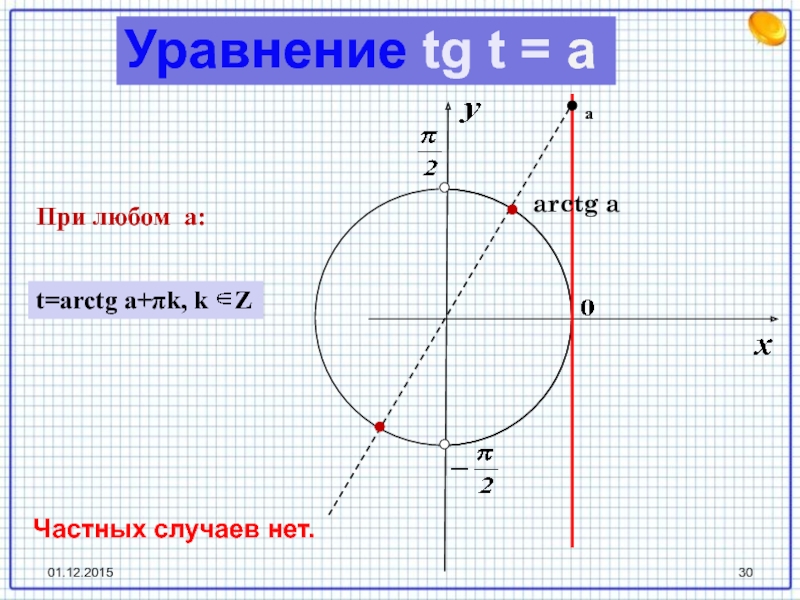
- 30. arctg aаПри любом a: Частных случаев нет.t=arctg a+πk, k ZУравнение tg t = a
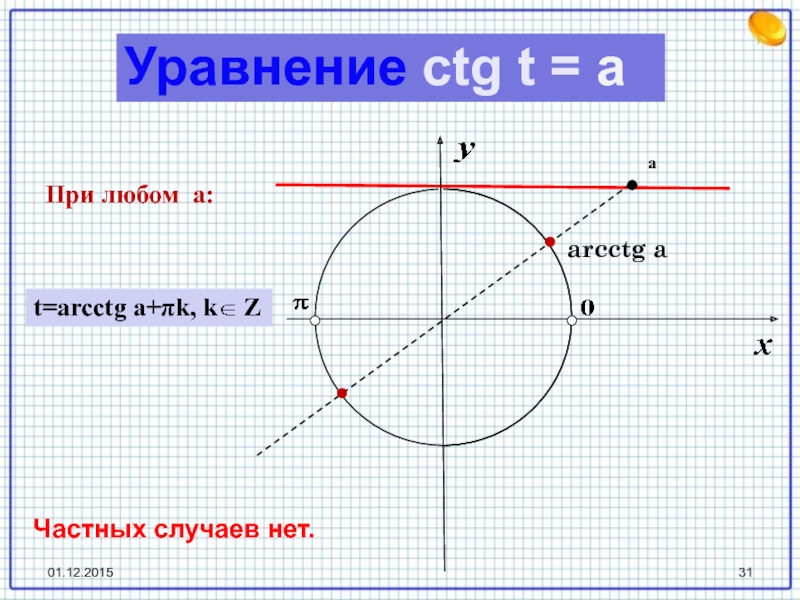
- 31. arcctg aаУравнение ctg t = aПри любом a: t=arcctg a+πk, k ZЧастных случаев нет.
- 32. Слайд 32
- 33. arctg (-a)= - arctg aarcctg (-a)= π - arcсtg a
- 34. tg (-a)= - tg a
- 35. 1 вариант2 вариантПотренируйся.
- 36. Спасибо за то, что стараешься!
arcsin (-a)= - arcsin aarccos (-a)= π - arccos aarctg (-a)= - arctg aarcctg (-a)= π - arcсtg aаrcsin1аrctg 1аrccosаrccos (-0,5)аrctg (- )аrcctg (-1)
Слайд 2arcsin (-a)= - arcsin a
arccos (-a)= π - arccos a
arctg (-a)=
- arctg a
arcctg (-a)= π - arcсtg a
arcctg (-a)= π - arcсtg a
аrcsin1
аrctg 1
аrccos
аrccos (-0,5)
аrctg (- )
аrcctg (-1)
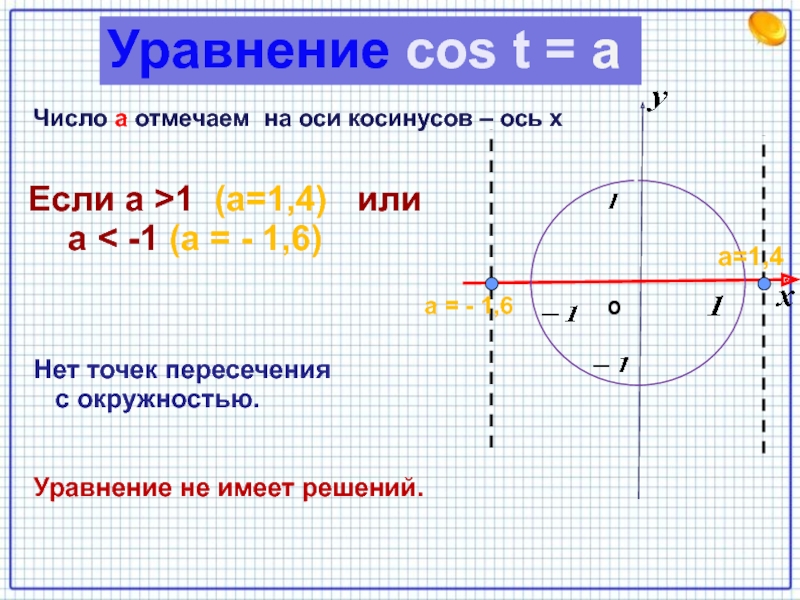
Слайд 3Если а >1 (а=1,4) или
а < -1
(а = - 1,6)
Нет точек пересечения
с окружностью.
Уравнение не имеет решений.
о
а=1,4
Уравнение sin t = a
а = - 1,6
Число а отмечаем на оси синусов – ось у
Слайд 7Решение уравнения sin t = a
Общий случай: -1< а
<1 ,то
Частный случай: sin t = 1 , то
sin t = 0 , то
sin t = - 1 , то
Если а > 1 или а < -1,то уравнение решений не имеет.
Частный случай: sin t = 1 , то
sin t = 0 , то
sin t = - 1 , то
Если а > 1 или а < -1,то уравнение решений не имеет.
Слайд 18Если а >1 (а=1,4) или а < -1 (а
= - 1,6)
Нет точек пересечения
с окружностью.
Уравнение не имеет решений.
о
а=1,4
а = - 1,6
Уравнение cos t = a
Число а отмечаем на оси косинусов – ось х
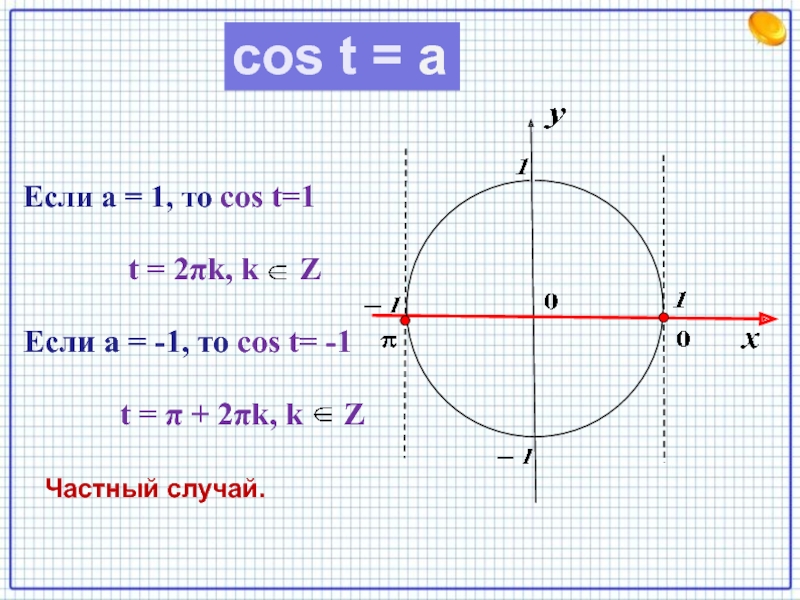
Слайд 19cos t = a
Частный случай.
Если а = 1, то cos t=1
t = 2πk, k Z
Если а = -1, то cos t= -1
t = π + 2πk, k Z
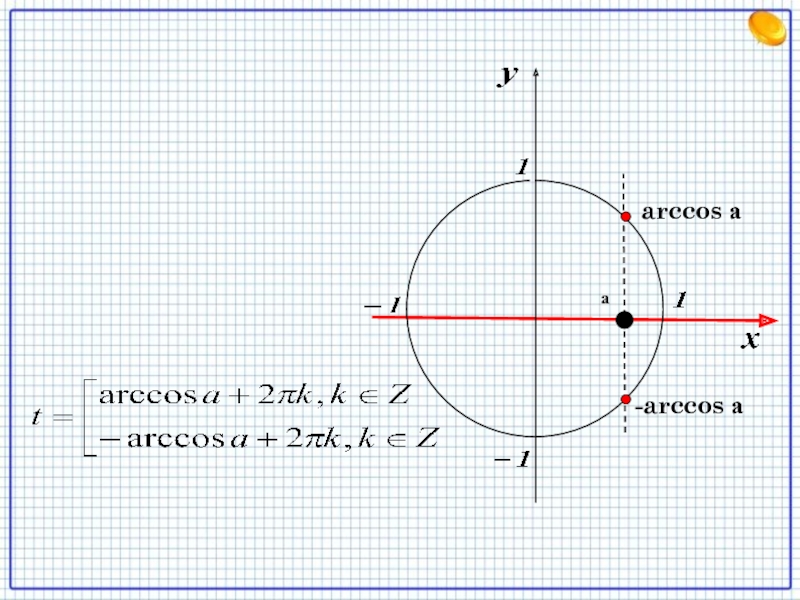
Слайд 22Решение уравнения cos t = a
Общий случай: -1< а
<1 ,то
Частный случай: cos t = 1 , то t = 2πk, k Z
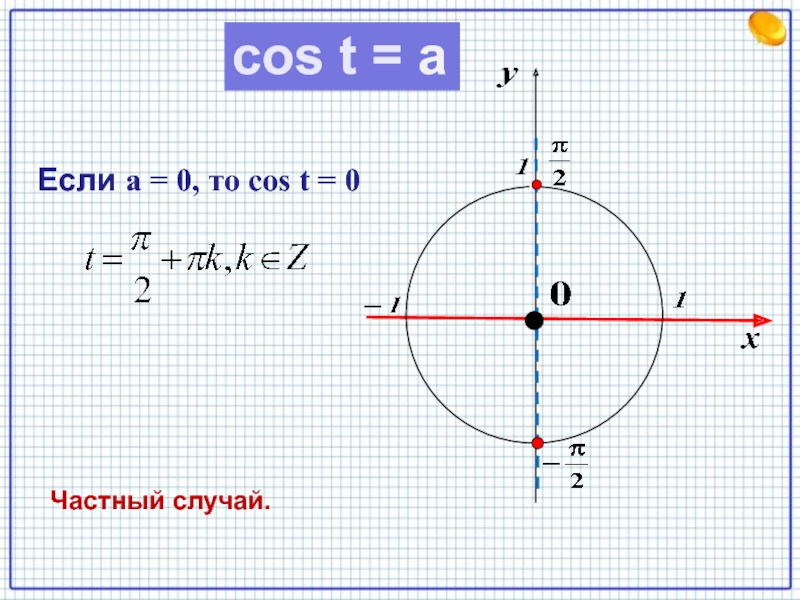
cos t = 0 , то
cos t = - 1 , то t = π + 2πk, k Z
Если ,то уравнение решений не имеет.
Частный случай: cos t = 1 , то t = 2πk, k Z
cos t = 0 , то
cos t = - 1 , то t = π + 2πk, k Z
Если ,то уравнение решений не имеет.