- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике 10-11 класс
Содержание
- 1. Презентация по математике 10-11 класс
- 2. ВАСDD1А1B1C12) пл.(ВB1C1С) ВК
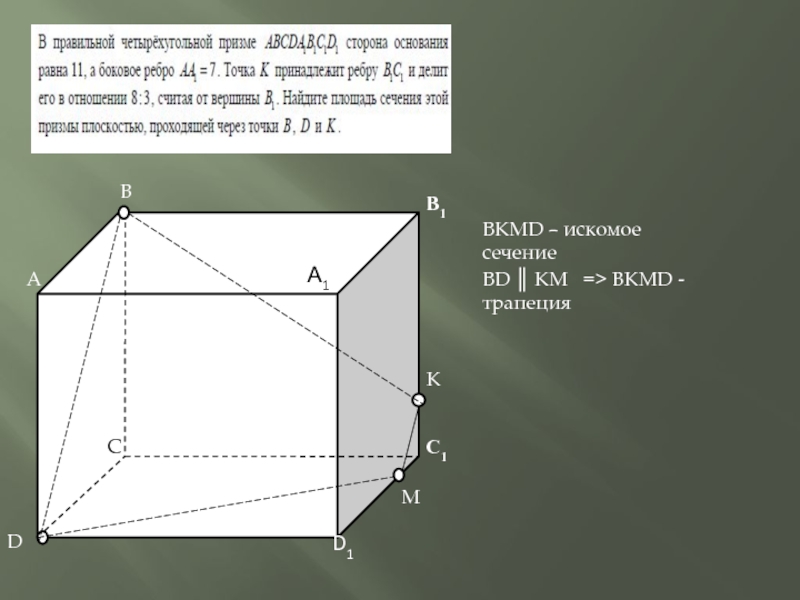
- 3. ВАСDD1А1B1C1KМВКМD – искомое сечениеВD ║ КМ => ВКМD - трапеция
- 4. А1 В1С1D1АСDВОА € пл. (АВВ1А1), О €
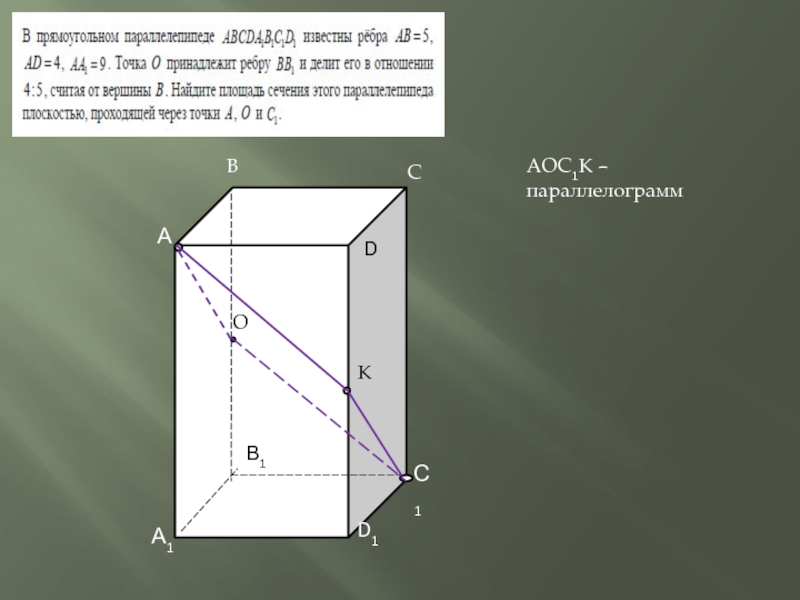
- 5. А1 В1С1D1АСDВОКAOС1K – параллелограмм
- 6. В основании прямой призмы ABCDA1B1C1D1 лежит квадрат
- 7. В основании прямой призмы ABCDA1B1C1D1 лежит квадрат
Слайд 1При построении сечения фигуры плоскостью необходимо помнить:
Через любые две точки
При пересечении нескольких параллельных плоскостей секущей плоскостью, линии пересечения параллельны;
Теорему Фалеса:
Соединять прямой можно только точки лежащие в одной плоскости;
Две непараллельные прямые в плоскости обязательно имеют одну точку пересечения.
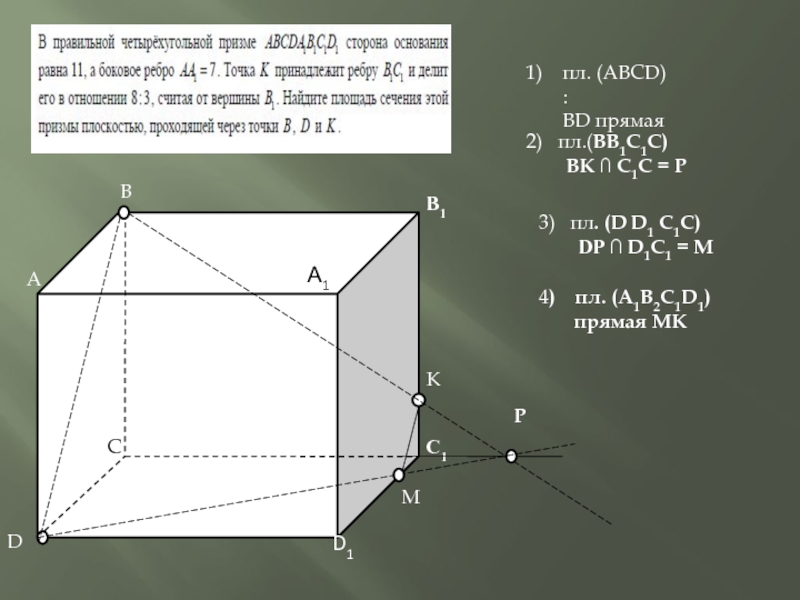
Слайд 2В
А
С
D
D1
А1
B1
C1
2) пл.(ВB1C1С)
ВК ∩ C1С = Р
K
Р
М
3)
DР ∩ D1C1 = М
4) пл. (А1В2С1D1)
прямая МК
пл. (АВСD) :
ВD прямая
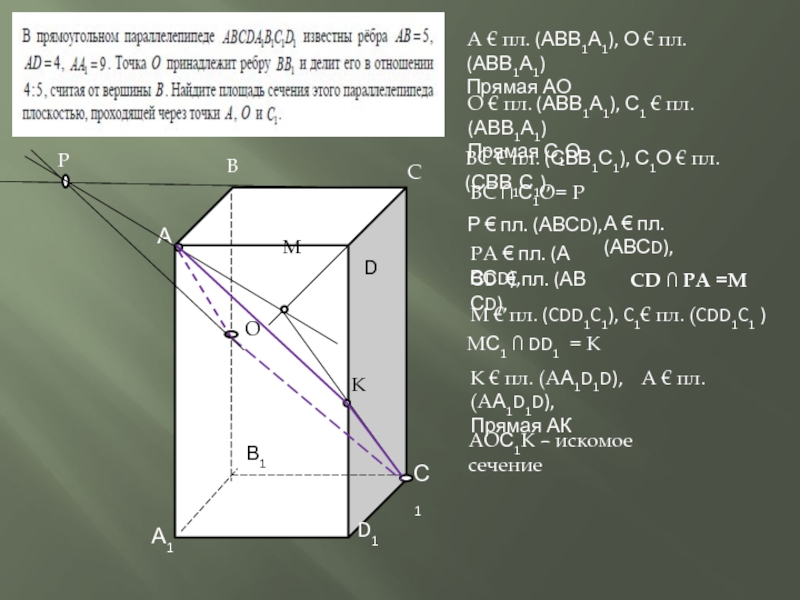
Слайд 4А1
В1
С1
D1
А
С
D
В
О
А € пл. (АВВ1А1), О € пл. (АВВ1А1)
Прямая АО
О
Прямая С1О
ВС ∩ С1О= Р
Р € пл. (АВСD),
Р
А € пл. (АВСD),
ВС € пл. (СВВ1С1), С1О € пл. (СВВ1С1),
РА € пл. (А ВСD),
СD € пл. (АВ СD),
М
CD ∩ РА =М
МС1 ∩ DD1 = K
К
К € пл. (АА1D1D), А € пл. (АА1D1D),
Прямая АК
АОС1К – искомое сечение
М € пл. (CDD1C1), C1€ пл. (CDD1C1 )
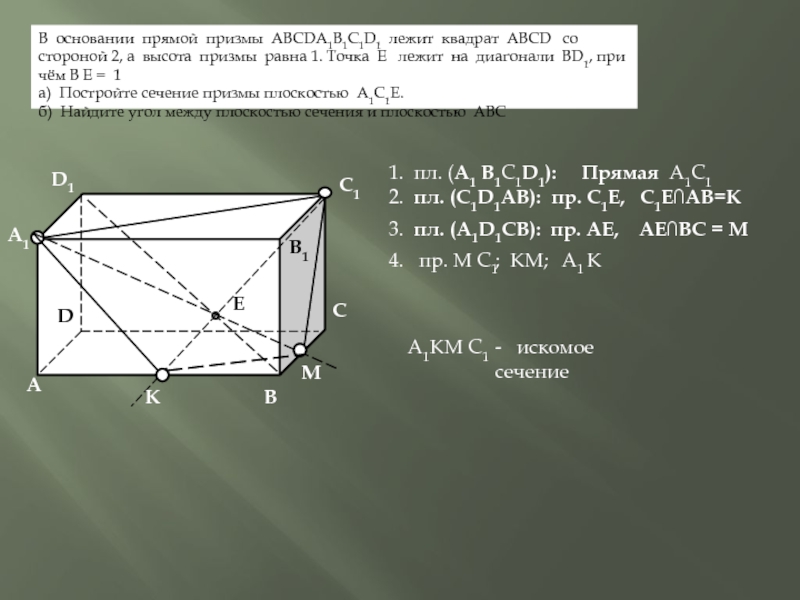
Слайд 6В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCD со стороной
а) Постройте сечение призмы плоскостью A1C1E.
б) Найдите угол между плоскостью сечения и плоскостью ABС
А
В
С
D
A1
B1
C1
D1
E
1. пл. (A1 B1C1D1): Прямая A1C1
2. пл. (C1D1AВ):
3. пл. (A1D1CB): пр. АЕ, АЕ∩ВС = М
К
М
; КМ;
4. пр. М C1
A1 К
A1КМ C1
- искомое сечение
пр. C1Е, C1Е∩АВ=К
Слайд 7В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCD со стороной
а) Постройте сечение призмы плоскостью A1C1E.
б) Найдите угол между плоскостью сечения и плоскостью ABС
А
В
С
D
A1
B1
C1
D1
E
К
М
АКМ C1
- искомое сечение
Р
H