Оглавление
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математической статистике
Содержание
- 1. Презентация по математической статистике
- 2. ОглавлениеГлава 1Представление статистических данныхГлава 2Точечные оценки параметров
- 3. Глава 1 Представление статистических данных1.1. Табличное
- 4. Табличное представление данныхЕсли имеется случайная величина ξ
- 5. Вариационным рядом относительных частот называют таблицу вида:
- 6. Графическое представление данныхДва способа графического представления статистических
- 7. Связь с понятиями теории вероятностиПусть
- 8. Статистические данные для двумерных случайных величинПусть дан
- 9. Задачи математической статистикиПуст
- 10. Глава 2 Точечные оценки параметров
- 11. Примеры и свойства оценокВажнейшим параметром любого распределения
- 12. Оценки наибольшего правдоподобия - случайная
- 13. Выборочный коэффициент корреляции Пусть задана выборка объема
- 14. Метод наименьших квадратов Рассмотрим для частного случая
- 15. Для нахождения значений a и b нужно
- 16. Выборочные прямые регрессииИмеется выборка для случайного вектораПрименяя
- 17. Глава 3 Интервальные оценки параметров распределения3.1.
- 18. Доверительный интервал для параметра a нормального распределения
- 19. Число равносильно уравнениюДля этого числа имеем
- 20. Доверительный интервал для параметра a нормального распределения
- 21. Z – преобразованиеФишер нашел интересное применение функции
- 22. Доверительный интервал для коэффициента корреляции нормально распределения
- 23. Число равносильно уравнению
- 24. Глава 4 Проверка статистических гипотез4.1. Основные понятия4.2.
- 25. Основные понятияПроверяемая статистическая гипотеза о случайной величине
- 26. Предположим, что заданы близкие к нулю числа
- 27. Во всех случаях сформулируем правило принятия решения.Если
- 28. Проверка гипотезы о равенстве математических ожиданий двух
- 29. Случай 1 имеет вид
- 30. Случай 2 имеет видВ данном случае
- 31. Проверка гипотезы о значимости коэффициента корреляции нормально
- 32. Проверка гипотезы о функции распределенияПусть
- 33. Решение принимается следующим образом. По таблице находим
- 34. Выбор из двух простых гипотезРассмотрим пример, показывающий
- 35. Приравниваем вероятность ошибки первого рода кЗаметим, что
- 36. Пусть задана вероятность ошибки второго рода
- 37. Можно ли сделать, чтобы одновременно вероятности ошибок
- 38. Глава 5 Вероятность и информатикаПонятие источникаЭнтропия
- 39. Тест Перейти к тестированию
ОглавлениеГлава 1Представление статистических данныхГлава 2Точечные оценки параметров распределения Глава 3Интервальные оценки параметров распределения Глава 4Проверка статистических гипотезГлава 5Вероятность и информатика
Слайд 2Оглавление
Глава 1
Представление статистических данных
Глава 2
Точечные оценки параметров распределения
Глава 3
Интервальные оценки
параметров распределения
Глава 4
Проверка статистических гипотез
Глава 5
Вероятность и информатика
Глава 4
Проверка статистических гипотез
Глава 5
Вероятность и информатика
Слайд 3Глава 1
Представление статистических данных
1.1. Табличное представление данных
1.2. Графическое представление данных
1.3.
Связь с понятиями теории вероятности
1.4. Статистические данные для двумерных случайных величин
1.5. Задачи математической статистики
1.4. Статистические данные для двумерных случайных величин
1.5. Задачи математической статистики
Слайд 4Табличное представление данных
Если имеется случайная величина ξ , закон распределения которой
неизвестен. И над ней можно провести сколь угодно испытаний. Допустим, что произведено n независимых испытаний, в результате которых получилась последовательность
y1, y2 , . . .,yn , такая последовательность называется выборкой объема n
Если n – велико, то над выборкой выполняются операции упрощения восприятия статистических данных, упорядочив значения по возрастанию
, или если в выборке есть повторы.
С любым значением можно связать число - абсолютная частота значения в выборке y1, y2 , . . .,yn . Это число испытаний в которых получилось значение
вариационный ряд, полученный по выборке y1, y2 , . . .,yn
Заметим, что
y1, y2 , . . .,yn , такая последовательность называется выборкой объема n
Если n – велико, то над выборкой выполняются операции упрощения восприятия статистических данных, упорядочив значения по возрастанию
, или если в выборке есть повторы.
С любым значением можно связать число - абсолютная частота значения в выборке y1, y2 , . . .,yn . Это число испытаний в которых получилось значение
вариационный ряд, полученный по выборке y1, y2 , . . .,yn
Заметим, что
Слайд 5Вариационным рядом относительных частот называют таблицу вида:
Где, значения выборки в порядке возрастания, а
частота события
Если ξ- непрерывна, вариационный ряд для выборки большого объема становится трудно обозримым. В этом случае выбирается числовой отрезок , содержащий все значения выборки, затем делят его на k равных частей, где
Подсчитаем относительную частоту попадания элементов выборки в любой из этих интервалов и составим таблицу.
Таблица относительных частот.
Иногда используется другой способ представления опытных данных – выборочная функция распределения , где справа стоит частота события
частота события
Если ξ- непрерывна, вариационный ряд для выборки большого объема становится трудно обозримым. В этом случае выбирается числовой отрезок , содержащий все значения выборки, затем делят его на k равных частей, где
Подсчитаем относительную частоту попадания элементов выборки в любой из этих интервалов и составим таблицу.
Таблица относительных частот.
Иногда используется другой способ представления опытных данных – выборочная функция распределения , где справа стоит частота события
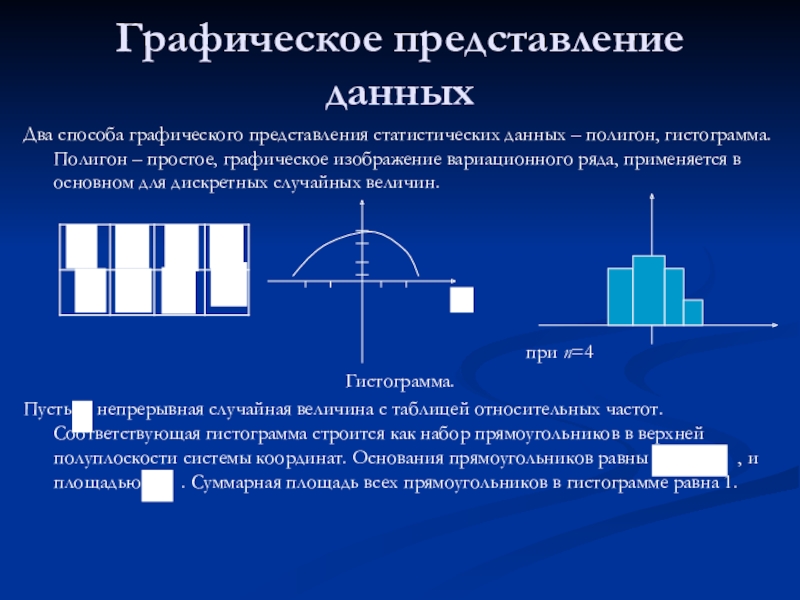
Слайд 6Графическое представление данных
Два способа графического представления статистических данных – полигон, гистограмма.
Полигон – простое, графическое изображение вариационного ряда, применяется в основном для дискретных случайных величин.
при n=4
Гистограмма.
Пусть непрерывная случайная величина с таблицей относительных частот. Соответствующая гистограмма строится как набор прямоугольников в верхней полуплоскости системы координат. Основания прямоугольников равны , и площадью . Суммарная площадь всех прямоугольников в гистограмме равна 1.
при n=4
Гистограмма.
Пусть непрерывная случайная величина с таблицей относительных частот. Соответствующая гистограмма строится как набор прямоугольников в верхней полуплоскости системы координат. Основания прямоугольников равны , и площадью . Суммарная площадь всех прямоугольников в гистограмме равна 1.
Слайд 7Связь с понятиями теории вероятности
Пусть случайная величина, имеющая функцию
распределения
По теореме Бернули значение выборочной функции распределения при сходится по вероятности к , таким образом выборочная функция распределения тесно связана с теоретической функцией распределения.
Если дискретная случайная величина, то по теореме Бернули вариационный ряд относительных частот при увеличении n сходится по вероятности к ряду распределения
. Также если непрерывная случайная величина, имеющая плотность вероятности, то гистограмма при увеличении числа сегментов, и уменьшении длины всех отрезков приближается к плотности вероятности .
Т.е. изучая выборки больших объемов будем получать точную информацию о законах распределения изучаемых случайных велечин.
По теореме Бернули значение выборочной функции распределения при сходится по вероятности к , таким образом выборочная функция распределения тесно связана с теоретической функцией распределения.
Если дискретная случайная величина, то по теореме Бернули вариационный ряд относительных частот при увеличении n сходится по вероятности к ряду распределения
. Также если непрерывная случайная величина, имеющая плотность вероятности, то гистограмма при увеличении числа сегментов, и уменьшении длины всех отрезков приближается к плотности вероятности .
Т.е. изучая выборки больших объемов будем получать точную информацию о законах распределения изучаемых случайных велечин.
Слайд 8Статистические данные для двумерных случайных величин
Пусть дан двумерный вектор
. Для этого двумерного случайного вектора выборка – последовательность пар чисел , которая записывается в виде таблицы.
Вариационный ряд строится так:
упорядочим по возрастанию множество первых и вторых элементов
Построим таблицу
- частота события
Для случайных векторов размерности больше 3
графические методы представления статистических
данных применяются редко, т.к. из-за сложности рисунка
теряется их наглядность.
Вариационный ряд строится так:
упорядочим по возрастанию множество первых и вторых элементов
Построим таблицу
- частота события
Для случайных векторов размерности больше 3
графические методы представления статистических
данных применяются редко, т.к. из-за сложности рисунка
теряется их наглядность.
Слайд 9Задачи математической статистики
Пуст
выборка для случайной величины . В самом общем случае цель математической статистики – по выборке сделать выводы о случайной величине
По выборке определить закон распределения величины
Получить по выборке приближенную оценку математического ожидания
Получить по выборке приближенную оценку дисперсии
Подтвердить или опровергнуть гипотезу о законе распределения
Точных ответов на такие вопросы получить нельзя, т.к выборка несет на себе черты случайности. В лучшем случае можно надеется на оценку вероятности сделанной ошибки. Это приводит к вопросам другого типа.
Найти вероятность того, что найденная оценка мат. ожидания попадет в интервал
По выборке определить закон распределения величины
Получить по выборке приближенную оценку математического ожидания
Получить по выборке приближенную оценку дисперсии
Подтвердить или опровергнуть гипотезу о законе распределения
Точных ответов на такие вопросы получить нельзя, т.к выборка несет на себе черты случайности. В лучшем случае можно надеется на оценку вероятности сделанной ошибки. Это приводит к вопросам другого типа.
Найти вероятность того, что найденная оценка мат. ожидания попадет в интервал
Слайд 10Глава 2
Точечные оценки параметров распределения
2.1. Примеры и свойства
оценок
2.2. Оценки наибольшего правдоподобия
2.3. Выборочный коэффициент корреляции
2.4. Метод наименьших квадратов
2.5. Выборочные прямые регрессии
2.2. Оценки наибольшего правдоподобия
2.3. Выборочный коэффициент корреляции
2.4. Метод наименьших квадратов
2.5. Выборочные прямые регрессии
Слайд 11Примеры и свойства оценок
Важнейшим параметром любого распределения является математическое
ожидание
. Оценим этот параметр с помощью законов больших чисел.
- среднеарифметическое значение выборки.
В статистике эта оценка называется выборочной
средней и обозначается .
Существуют и другие оценки
Для дисперсии
- выборочная дисперсия.
- исправленная выборочная дисперсия.
Оценка несмещенная, если . Оценка состоятельная, если
. Оценим этот параметр с помощью законов больших чисел.
- среднеарифметическое значение выборки.
В статистике эта оценка называется выборочной
средней и обозначается .
Существуют и другие оценки
Для дисперсии
- выборочная дисперсия.
- исправленная выборочная дисперсия.
Оценка несмещенная, если . Оценка состоятельная, если
Слайд 12Оценки наибольшего правдоподобия
- случайная величина, с известным законом
распределения, зависящем от . Требуется найти оценку для параметра по выборке
1.сл. Если - непрерывная случайная величина с плотностью вероятности , то функцией правдоподобия называется функция, задаваемая следующим образом:
2.сл. Если - дискретная величина, с законом распределения ,то функция правдоподобия выглядит как и в случае 1.
Определение: Оценкой наибольшего правдоподобия – значение переменной , при котором L имеет наибольшее значение.
Обозначим оценку наибольшего правдоподобия
- то значение параметра, при котором, получившаяся на опыте выборка наиболее вероятна.
Для нахождения оценки наибольшего правдоподобия нужно исследовать L на максимум.
L=max, тогда и только тогда, когда
Необходимый признак экстремума
Для нахождения оценки наибольшего правдоподобия надо составить функцию L и решить уравнение (1) относительно
1.сл. Если - непрерывная случайная величина с плотностью вероятности , то функцией правдоподобия называется функция, задаваемая следующим образом:
2.сл. Если - дискретная величина, с законом распределения ,то функция правдоподобия выглядит как и в случае 1.
Определение: Оценкой наибольшего правдоподобия – значение переменной , при котором L имеет наибольшее значение.
Обозначим оценку наибольшего правдоподобия
- то значение параметра, при котором, получившаяся на опыте выборка наиболее вероятна.
Для нахождения оценки наибольшего правдоподобия нужно исследовать L на максимум.
L=max, тогда и только тогда, когда
Необходимый признак экстремума
Для нахождения оценки наибольшего правдоподобия надо составить функцию L и решить уравнение (1) относительно
Слайд 13Выборочный коэффициент корреляции
Пусть задана выборка объема n для системы случайных величин
Требуется оценить по выборке коэффициент корреляции
Будем их использовать в качестве оценок для средне квадратичных отклонений величин
. Для оценки корреляционного момента будем использовать:
Выборочным коэффициентом корреляции называется оценка вида
Свойства
1.
2. состоятельная оценка коэффициента корреляции
3. смещенная оценка коэффициента корреляции, причем смещение стремится к 0, при n стремящимся к бесконечности.
Если близка к 1, то имеется сильная прямопропорциональная зависимость между
Если близко к -1, то зависимость между обратнопропорциональная
Если близко к 0, то данные не подтверждают наличие линейной зависимости между
Слайд 14Метод наименьших квадратов
Рассмотрим для частного случая линейной функции f(x)=a+bx, где
a и b – неизвестны.
n различными способами выбрали значение аргумента и с помощью измерительного прибора определили соответствующее значение функции
Получили таблицу для случайного вектора.
Столбцам таблицы соответствует n точек на плоскости, которые
лежат на одной прямой y=a+bx, но т.к. приборы не точны, точки
почти всегда не будут лежать на одной прямой.
С геометрической точки зрения, задача в том, чтобы найти прямую, которая приближает точки наилучшем способом.
Для измерения расстояния между совокупностью точек и прямой можно использовать функцию:
Согласно методу наименьших квадратов прямой наилучшего приближения считают такую прямую, для которой величина S(a,b) является наименьшей из всех возможных.
Можно доказать, что такая прямая существует, и единственна.
Доказательство.
n различными способами выбрали значение аргумента и с помощью измерительного прибора определили соответствующее значение функции
Получили таблицу для случайного вектора.
Столбцам таблицы соответствует n точек на плоскости, которые
лежат на одной прямой y=a+bx, но т.к. приборы не точны, точки
почти всегда не будут лежать на одной прямой.
С геометрической точки зрения, задача в том, чтобы найти прямую, которая приближает точки наилучшем способом.
Для измерения расстояния между совокупностью точек и прямой можно использовать функцию:
Согласно методу наименьших квадратов прямой наилучшего приближения считают такую прямую, для которой величина S(a,b) является наименьшей из всех возможных.
Можно доказать, что такая прямая существует, и единственна.
Доказательство.
Слайд 15Для нахождения значений a и b нужно исследовать функцию S(a,b) на
минимум.
В точке минимума выполняется:
Полученная система имеет единственное решение и
Величины и можно рассматривать, как статистические оценки неизвестных параметров a и b. Эти оценки являются несмещенными и состоятельными.
Если измерительный прибор не имеет систематической ошибки, и ошибка измерения распределена нормально, то оценки и являются оценками наибольшего правдоподобия для параметров a и b.
В точке минимума выполняется:
Полученная система имеет единственное решение и
Величины и можно рассматривать, как статистические оценки неизвестных параметров a и b. Эти оценки являются несмещенными и состоятельными.
Если измерительный прибор не имеет систематической ошибки, и ошибка измерения распределена нормально, то оценки и являются оценками наибольшего правдоподобия для параметров a и b.
Слайд 16Выборочные прямые регрессии
Имеется выборка для случайного вектора
Применяя к ней метод наименьших
квадратов, получим прямую наилучшего приближения y=a+bx. Оказывается эта прямая тесно связана с ранее рассмотренными оценками.
Проверка этой формулы осуществляется подстановкой данных значений
в полученную нами систему.
Прямая (1) называется выборочной прямой регрессии на
Меняя местами и получим уравнение прямой регрессии на
Проверка этой формулы осуществляется подстановкой данных значений
в полученную нами систему.
Прямая (1) называется выборочной прямой регрессии на
Меняя местами и получим уравнение прямой регрессии на
Слайд 17Глава 3
Интервальные оценки параметров распределения
3.1. Доверительный интервал для параметра a
нормального распределения при известном
3.2. Доверительный интервал для параметра a нормального распределения при неизвестном
3.3. Z – преобразование
3.4. Доверительный интервал для коэффициента корреляции нормально распределения случайного вектора
3.2. Доверительный интервал для параметра a нормального распределения при неизвестном
3.3. Z – преобразование
3.4. Доверительный интервал для коэффициента корреляции нормально распределения случайного вектора
Слайд 18Доверительный интервал для параметра a нормального распределения при известном
Пусть случайная
величина распределена по нормальному закону с параметрами и
при этом a – неизвестна, - известна. Требуется по заданной выборке для случайной величины найти доверительный интервал для параметра a, соответствующий заданной доверительной вероятности .
Рассмотрим выборочное среднее
Элементы выборки – независимые случайные величины, распределенные по нормальному закону с параметрами a и . Сумма нормально распределенных величин – нормально распределенная случайная величина. А линейная функция от нормальной случайной величина – нормально распределена. Поэтому случайная величина распределена по нормальному закону.
Рассмотрим
Таким образом
Значит
при этом a – неизвестна, - известна. Требуется по заданной выборке для случайной величины найти доверительный интервал для параметра a, соответствующий заданной доверительной вероятности .
Рассмотрим выборочное среднее
Элементы выборки – независимые случайные величины, распределенные по нормальному закону с параметрами a и . Сумма нормально распределенных величин – нормально распределенная случайная величина. А линейная функция от нормальной случайной величина – нормально распределена. Поэтому случайная величина распределена по нормальному закону.
Рассмотрим
Таким образом
Значит
Слайд 20Доверительный интервал для параметра a нормального распределения при неизвестном
Пусть величина
распределена по нормальному закону с параметрами a и причем оба не известны. Задана выборка и доверительная вероятность
Требуется найти доверительный интервал для a, соответствующий вероятности
Рассмотрим случайную величину
Теорема: случайная величина распределена по закону Стьюдента с параметром n-1.
Существует единственное положительное число , удовлетворяющее условию:
По теореме Стьюдента:
Тогда доверительный интервал выглядит следующим образом:
Требуется найти доверительный интервал для a, соответствующий вероятности
Рассмотрим случайную величину
Теорема: случайная величина распределена по закону Стьюдента с параметром n-1.
Существует единственное положительное число , удовлетворяющее условию:
По теореме Стьюдента:
Тогда доверительный интервал выглядит следующим образом:
Слайд 21Z – преобразование
Фишер нашел интересное применение функции
, которая носит название Z преобразование Фишера. Эта функция нечетная, монотонная на интервале (-1; 1) и определяет взаимно однозначное соответствие между интервалом (-1; 1) и множеством R.
Обратная функция к Z преобразованию – монотонно возрастающая , задается равенством:
Заметим ,что функции Z и достаточно просты и могут быть вычислены с помощью калькулятора.
Обратная функция к Z преобразованию – монотонно возрастающая , задается равенством:
Заметим ,что функции Z и достаточно просты и могут быть вычислены с помощью калькулятора.
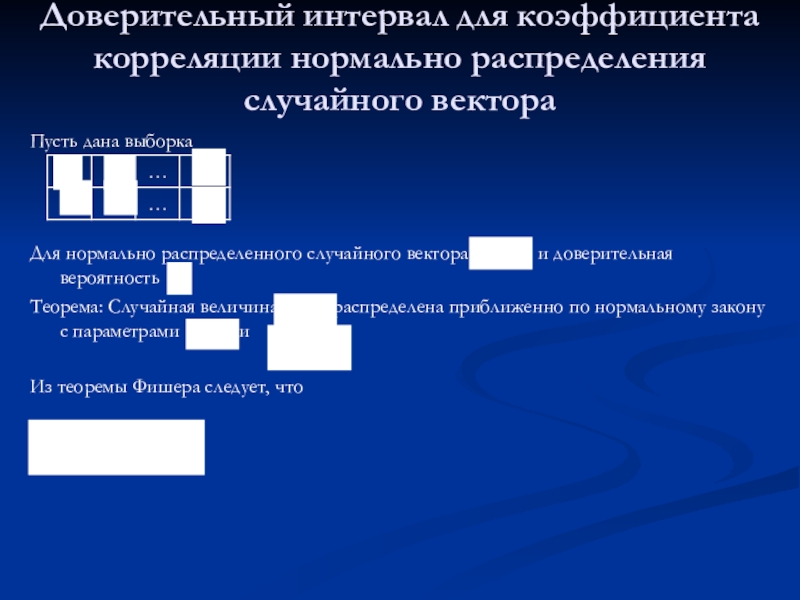
Слайд 22Доверительный интервал для коэффициента корреляции нормально распределения случайного вектора
Пусть дана выборка
Для нормально распределенного случайного вектора , и доверительная вероятность
Теорема: Случайная величина распределена приближенно по нормальному закону с параметрами и
Из теоремы Фишера следует, что
Слайд 23Число равносильно уравнению
, тогда
Доверительный интервал для есть
Учитывая монотонность функции Z неравенство для выглядит так:
Таким образом доверительный интервал для параметра выглядит так::
Доверительный интервал для есть
Учитывая монотонность функции Z неравенство для выглядит так:
Таким образом доверительный интервал для параметра выглядит так::
Слайд 24Глава 4
Проверка статистических гипотез
4.1. Основные понятия
4.2. Проверка гипотезы о равенстве математических
ожиданий двух нормально распределенных случайных величин
4.3. Проверка гипотезы о значимости коэффициента корреляции нормально распределенного случайного вектора
4.4. Проверка гипотезы о функции распределения
4.5. Выбор из двух простых гипотез
4.3. Проверка гипотезы о значимости коэффициента корреляции нормально распределенного случайного вектора
4.4. Проверка гипотезы о функции распределения
4.5. Выбор из двух простых гипотез
Слайд 25Основные понятия
Проверяемая статистическая гипотеза о случайной величине или случайном векторе называется
основной и обозначается . Часто при проверке основной гипотезы вводят противоречащую ей гипотезу, которая называется альтернативной и обозначается .
Для проверки статистической гипотезы нужно сформулировать разумное правило принятия решения о том, какую из двух гипотез подтверждает данная выборка. Возможно 4 варианта:
Верна , но принимается
Верна , но принимается
Верна , и она принимается
Верна , и она принимается
В случаях 1 и 2 совершаются ошибки, которые называют соответственно ошибкой первого рода и ошибкой второго рода. Основная идея при формулировке правила принятия решения состоит в том, чтобы уменьшить вероятность ошибки первого рода, а если возможно, то и вероятность ошибки второго рода.
Для проверки статистической гипотезы нужно сформулировать разумное правило принятия решения о том, какую из двух гипотез подтверждает данная выборка. Возможно 4 варианта:
Верна , но принимается
Верна , но принимается
Верна , и она принимается
Верна , и она принимается
В случаях 1 и 2 совершаются ошибки, которые называют соответственно ошибкой первого рода и ошибкой второго рода. Основная идея при формулировке правила принятия решения состоит в том, чтобы уменьшить вероятность ошибки первого рода, а если возможно, то и вероятность ошибки второго рода.
Слайд 26Предположим, что заданы близкие к нулю числа и
, причем
Число называется уровнем значимости.
Пусть гипотезы и утверждают нечто о поведении случайной величины и с каждой выборкой связано некоторое число называемое критерием. Критерий стараются подобрать так, чтобы закон распределения случайной величины при условии истинности был достаточно простым. В таких случаях удается сформулировать правило принятия решения с таким расчетом, чтобы вероятность ошибки первого рода равнялась .
Допустим, что при справедливости , - непрерывная случайная величина, с известной плотностью вероятности
Определение Критической областью, отвечающей уровню значимости называется конечный или бесконечный интервал (a, b), для которого выполняется равенство:
Если , то критическая область – левосторонняя, если , то критическая область – правосторонняя. Критическая область может быть двусторонней, в этом случае должно выполняться:
т.е. вероятность попадания критерия в критическую
область должна равняться
Число называется уровнем значимости.
Пусть гипотезы и утверждают нечто о поведении случайной величины и с каждой выборкой связано некоторое число называемое критерием. Критерий стараются подобрать так, чтобы закон распределения случайной величины при условии истинности был достаточно простым. В таких случаях удается сформулировать правило принятия решения с таким расчетом, чтобы вероятность ошибки первого рода равнялась .
Допустим, что при справедливости , - непрерывная случайная величина, с известной плотностью вероятности
Определение Критической областью, отвечающей уровню значимости называется конечный или бесконечный интервал (a, b), для которого выполняется равенство:
Если , то критическая область – левосторонняя, если , то критическая область – правосторонняя. Критическая область может быть двусторонней, в этом случае должно выполняться:
т.е. вероятность попадания критерия в критическую
область должна равняться
Слайд 27Во всех случаях сформулируем правило принятия решения.
Если критерий, вычисленный по данной
выборке попал в критическую область, то принимаем иначе принимаем .
При таком правиле вероятность ошибки первого рода равна . Критическую область можно выбрать многими способами. В некоторых случаях используя особенность функции f(x) удается выбрать критическую область так, чтобы вероятность ошибки второго рода была наименьшей, при вероятности ошибки первого рода равной
В таких случаях разумно выбирать именно такую критическую область.
При таком правиле вероятность ошибки первого рода равна . Критическую область можно выбрать многими способами. В некоторых случаях используя особенность функции f(x) удается выбрать критическую область так, чтобы вероятность ошибки второго рода была наименьшей, при вероятности ошибки первого рода равной
В таких случаях разумно выбирать именно такую критическую область.
Слайд 28Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных случайных величин
Пусть
даны выборки для двух нормально распределенных случайных величин и с
известными дисперсиями и . Также задан уровень
значимости L.
Требуется проверить гипотезу о равенстве математических ожиданий величин и .
Основная гипотеза есть , что эквивалентно равенству
В качестве критерия возьмем нормально распределенную случайную величину
при справедливости гипотезы и при . Таким образом при справедливости имеем, что
Формулировка правила принятия решения зависит от вида альтернативной гипотезы.
Рассмотрим 2 возможных вида гипотезы
Случай 1
Случай 2
известными дисперсиями и . Также задан уровень
значимости L.
Требуется проверить гипотезу о равенстве математических ожиданий величин и .
Основная гипотеза есть , что эквивалентно равенству
В качестве критерия возьмем нормально распределенную случайную величину
при справедливости гипотезы и при . Таким образом при справедливости имеем, что
Формулировка правила принятия решения зависит от вида альтернативной гипотезы.
Рассмотрим 2 возможных вида гипотезы
Случай 1
Случай 2
Слайд 29Случай 1
имеет вид
. Таким образом гипотеза равносильна . Поэтому в данном случае надо выбрать правостороннюю критическую область.
Пусть число удовлетворяющее и оно находится по таблице.
Правило принятия решения выглядит следующим образом:
Если , то принимается гипотеза , иначе принимается
Пусть число удовлетворяющее и оно находится по таблице.
Правило принятия решения выглядит следующим образом:
Если , то принимается гипотеза , иначе принимается
Слайд 30Случай 2
имеет вид
В данном случае лучше пользоваться двусторонней критической
областью. Найдем число
следующим образом:
В качестве критической области возьмем множество
Правило принятия решения выглядит так:
если , то принимаем гипотезу , иначе принимаем
следующим образом:
В качестве критической области возьмем множество
Правило принятия решения выглядит так:
если , то принимаем гипотезу , иначе принимаем
Слайд 31Проверка гипотезы о значимости коэффициента корреляции нормально распределенного случайного вектора
Предположим, что
дана выборка , для нормально распределенного вектора. По выборке найден выборочный коэффициент корреляции
В силу случайных факторов почти всегда не равна нулю. Возникает вопрос: можно ли по выборке сделать вывод, что коэффициент корреляции отличен от нуля?
Надо проверить гипотезу : при данном условии значимости
В качестве возьмем
Критерий выглядит следующим образом:
Теорема: Если , то величина K распределена по закону Стьюдента с параметром n-2 ( )
Выбираем двустороннюю критическую область . Число находится так
Правило принятия решения выглядит так:
если , то принимаем гипотезу , иначе принимаем
В силу случайных факторов почти всегда не равна нулю. Возникает вопрос: можно ли по выборке сделать вывод, что коэффициент корреляции отличен от нуля?
Надо проверить гипотезу : при данном условии значимости
В качестве возьмем
Критерий выглядит следующим образом:
Теорема: Если , то величина K распределена по закону Стьюдента с параметром n-2 ( )
Выбираем двустороннюю критическую область . Число находится так
Правило принятия решения выглядит так:
если , то принимаем гипотезу , иначе принимаем
Слайд 32Проверка гипотезы о функции распределения
Пусть
выборка для случайной величины и имеются основания предполагать, что величина имеет функцию распределения F, где F – неизвестная функция. Подтверждает ли выборка это предположение или противоречит ему?
В качестве возьмем утверждение , а в качестве возьмем
Для решения задачи используют так называемый критерий “ хи-квадрат ”.
Построим таблицу частот и вероятностей следующим образом. Разобьем числовую прямую на m интервалов и посчитаем частоту попадания элементов выборки в каждый интервал, а также вероятность попадания случайной величины в каждый интервал. Получим таблицу вида:
Замечание: при выборе интервалов нужно
руководствоваться смыслом задачи и тем, чтобы в каждом
интервале было как минимум 10 точек.
В качеству критерия возьмем величину
Теорема: если гипотеза верна, то случайная величина k распределена приближенно по закону
В качестве возьмем утверждение , а в качестве возьмем
Для решения задачи используют так называемый критерий “ хи-квадрат ”.
Построим таблицу частот и вероятностей следующим образом. Разобьем числовую прямую на m интервалов и посчитаем частоту попадания элементов выборки в каждый интервал, а также вероятность попадания случайной величины в каждый интервал. Получим таблицу вида:
Замечание: при выборе интервалов нужно
руководствоваться смыслом задачи и тем, чтобы в каждом
интервале было как минимум 10 точек.
В качеству критерия возьмем величину
Теорема: если гипотеза верна, то случайная величина k распределена приближенно по закону
Слайд 33Решение принимается следующим образом. По таблице находим число
так, чтобы было правосторонней критической областью для распределения
вычисляем значение критерия
Если , то принимаем иначе принимаем альтернативную гипотезу.
Замечание: критерий можно применять и тогда, когда функция распределения F зависит от нескольких параметров, значения которых неизвестны. Например, если F - функция распределения нормальной случайной величины с неизвестными параметрами .
Тогда при условии истинности имеем , а все остальное остается без изменений.
вычисляем значение критерия
Если , то принимаем иначе принимаем альтернативную гипотезу.
Замечание: критерий можно применять и тогда, когда функция распределения F зависит от нескольких параметров, значения которых неизвестны. Например, если F - функция распределения нормальной случайной величины с неизвестными параметрами .
Тогда при условии истинности имеем , а все остальное остается без изменений.
Слайд 34Выбор из двух простых гипотез
Рассмотрим пример, показывающий как наряду с вероятностью
ошибки первого рода также можно учитывать вероятность ошибки второго рода.
Пусть имеется случайная величина , распределенная по нормальному закону, причем
-неизвестна. И имеется основание предполагать, что справедлива одна из двух гипотез
Какую из гипотез подтверждает данная выборка:
Зафиксируем вероятность ошибки первого рода
Схема принятия решения.
Выбираем точку С между и вычисляем . Если , то принимаем , иначе принимаем
Выбор числа С осуществляется таким образом, чтобы вероятность ошибки первого рода равнялась
Пусть имеется случайная величина , распределенная по нормальному закону, причем
-неизвестна. И имеется основание предполагать, что справедлива одна из двух гипотез
Какую из гипотез подтверждает данная выборка:
Зафиксируем вероятность ошибки первого рода
Схема принятия решения.
Выбираем точку С между и вычисляем . Если , то принимаем , иначе принимаем
Выбор числа С осуществляется таким образом, чтобы вероятность ошибки первого рода равнялась
Слайд 35Приравниваем вероятность ошибки первого рода к
Заметим, что если верна гипотеза
, то подчинена нормальному закону распределения с параметрами , поэтому и соответственно
Пусть единственное решение уравнения . Это уравнение равносильно
Из единственности числа следует
Пусть единственное решение уравнения . Это уравнение равносильно
Из единственности числа следует
Слайд 36Пусть задана вероятность ошибки второго рода . Для этой вероятности
получаем следующее уравнение:
При справедливости имеем, что:
Выбираем в качестве с – число:
Таким образом можно сделать вероятность ошибки второго рода равной
При справедливости имеем, что:
Выбираем в качестве с – число:
Таким образом можно сделать вероятность ошибки второго рода равной
Слайд 37Можно ли сделать, чтобы одновременно вероятности ошибок первого и второго рода
равнялись соответственно и
При фиксированном объеме выборки этого добиться невозможно, т.к (1) и (2) – несовместимы. Но по любым и можно найти объем выборки, при котором вероятности ошибок равны соответственно и . Для этого нужно решить систему уравнений относительно
При фиксированном объеме выборки этого добиться невозможно, т.к (1) и (2) – несовместимы. Но по любым и можно найти объем выборки, при котором вероятности ошибок равны соответственно и . Для этого нужно решить систему уравнений относительно
Слайд 38Глава 5
Вероятность и информатика
Понятие источника
Энтропия источника
Возможность передачи информации
Компьютерное моделирование случайных
величин
Понятие о методе Монте-Карло
Особенности метода Монте-Карло
Понятие о методе Монте-Карло
Особенности метода Монте-Карло