- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии в 10 классе на темуПерпендикулярность прямой и плоскости.
Содержание
- 1. Презентация по геометрии в 10 классе на темуПерпендикулярность прямой и плоскости.
- 2. Две прямые в пространстве называются перпендикулярными ,если
- 3. лемма: Если одна из двух параллельных прямых
- 4. АВСDА 1В 1С1D1Докажите, что DC B1C1
- 5. Прямая называется перпендикулярной к плоскости, если она
- 6. НациональныйПарк Чехии.
- 7. Эрмитаж
- 8. Парламент на Дунае в Венгрии
- 9. Танцующий дом Падающая башня
- 10. Ученик дал следующее определение: «Прямая, пересекающая плоскость,
- 11. Связь между параллельностью прямых и их перпендикулярностью
- 12. Теорема: Если две прямые перпендикулярны к плоскости,
- 13. Решение задач.№ 119АОDBCДано: ОА ┴ (ОВС)ОА= ОDДокажите:
- 14. № 120 Дано: АВСD- квадрат. АВ= а,
- 15. Итог урока : Д / з :
Слайд 2Две прямые в пространстве называются перпендикулярными ,если угол между ними равен
а с
c
a
α
Перпендикулярные прямые в пространстве.
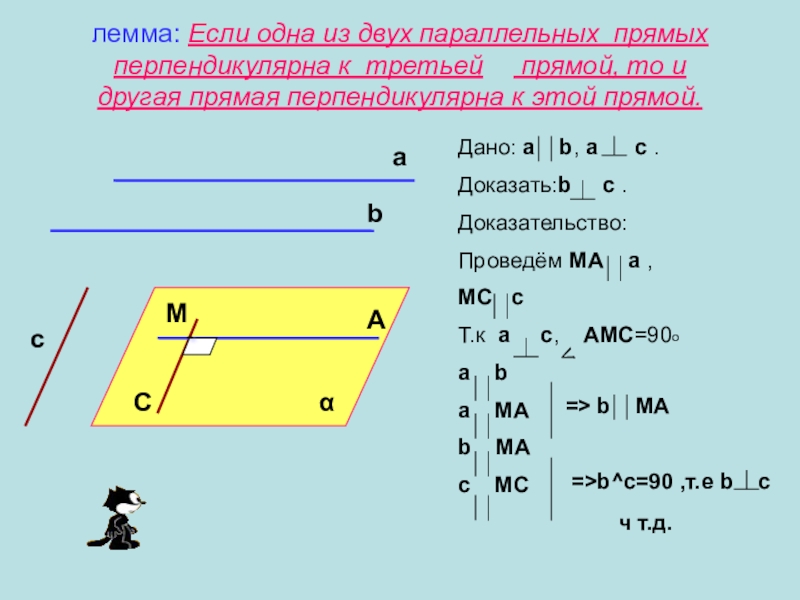
Слайд 3лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой,
.
М
α
А
С
с
b
a
Дано: а b, a c .
Доказать:b c .
Доказательство:
Проведём МА а ,
МС с
Т.к а с, AMC=90
a b
a MA
b MA
c MC
ч т.д.
о
<
=> b MA
=>b^c=90 ,т.е b c
Слайд 4
А
В
С
D
А 1
В 1
С1
D1
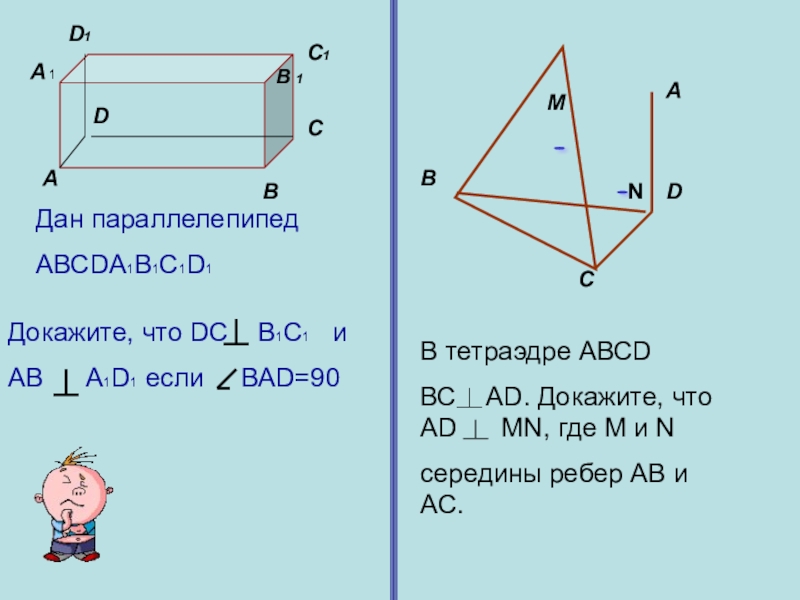
Докажите, что DC B1C1 и
AB
А
D
В
С
В тетраэдре АВСD
ВС АD. Докажите, что АD MN, где М и N
середины ребер АВ и АС.
М
.
.
N
Дан параллелепипед
АВСDA1B1C1D1
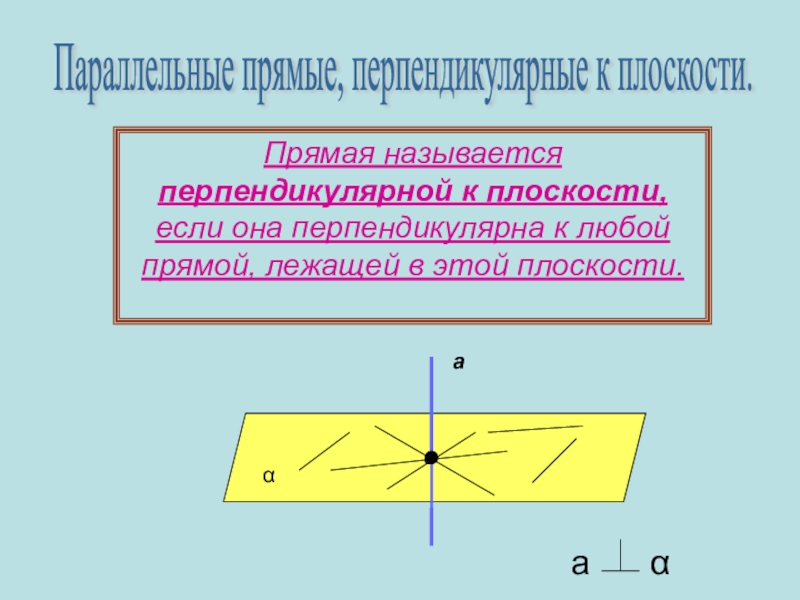
Слайд 5Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой,
а α
Параллельные прямые, перпендикулярные к плоскости.
а
α
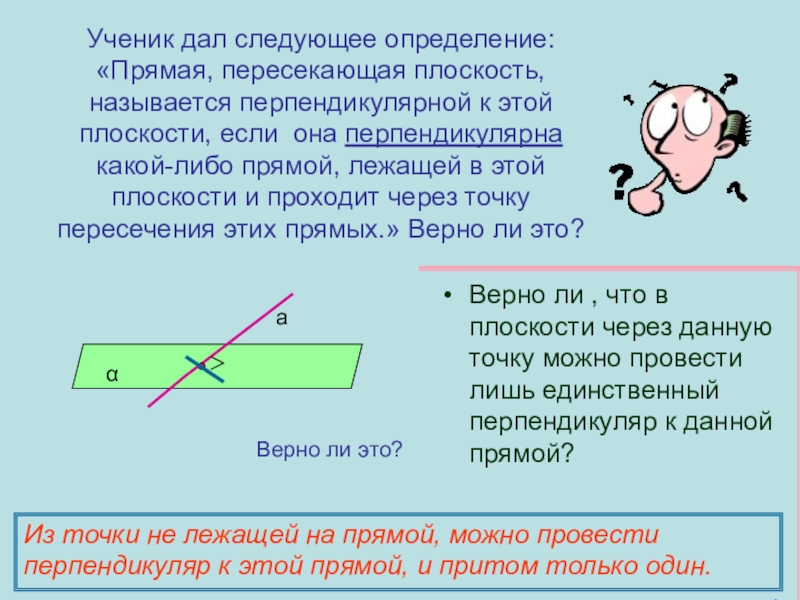
Слайд 10Ученик дал следующее определение: «Прямая, пересекающая плоскость, называется перпендикулярной к этой плоскости, если она
Верно ли , что в плоскости через данную точку можно провести лишь единственный перпендикуляр к данной прямой?
α
а
Из точки не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Верно ли это?
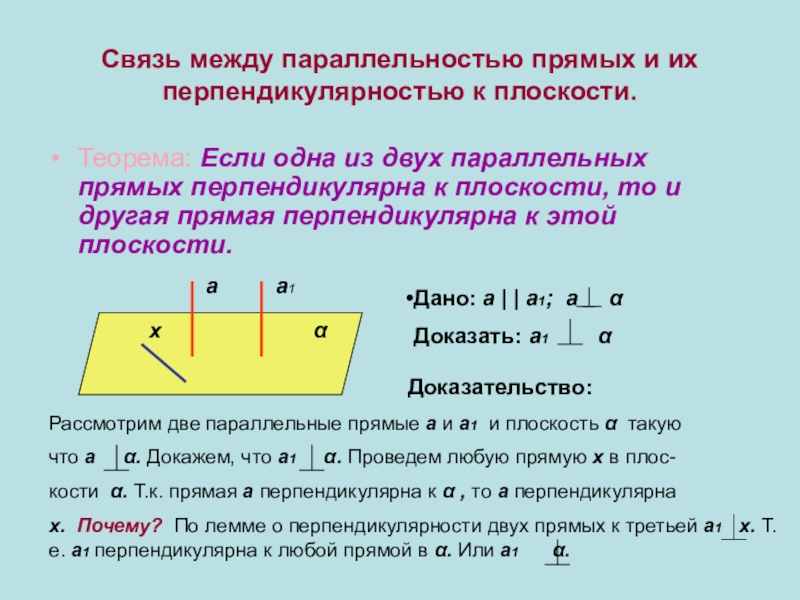
Слайд 11Связь между параллельностью прямых и их перпендикулярностью к плоскости.
Теорема: Если одна
а1
а
α
х
Дано: а | | а1; а α
Доказать: а1 α
Доказательство:
Рассмотрим две параллельные прямые а и а1 и плоскость α такую
что а α. Докажем, что а1 α. Проведем любую прямую х в плос-
кости α. Т.к. прямая а перпендикулярна к α , то а перпендикулярна
х. Почему? По лемме о перпендикулярности двух прямых к третьей а1 х. Т.е. а1 перпендикулярна к любой прямой в α. Или а1 α.
Слайд 12Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
Доказать: а | | b
а
b
α
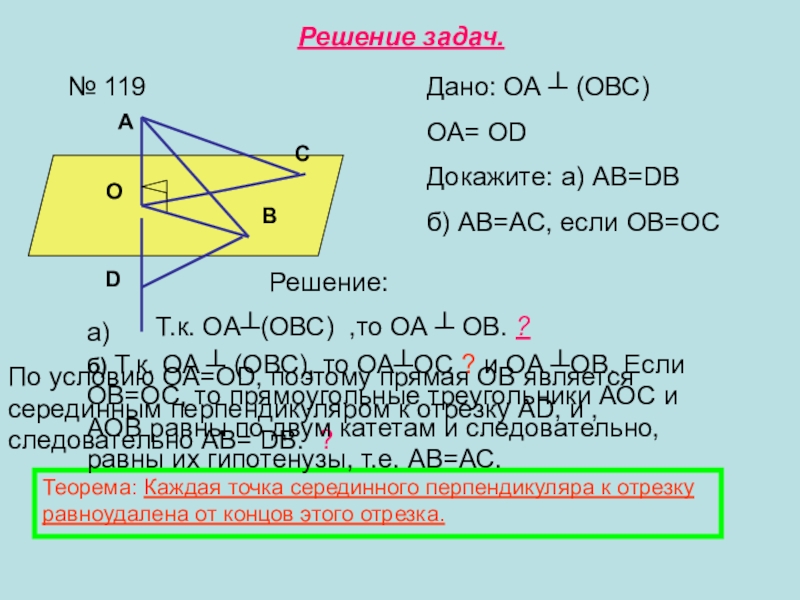
Слайд 13Решение задач.
№ 119
А
О
D
B
C
Дано: ОА ┴ (ОВС)
ОА= ОD
Докажите: а) АВ=DB
б) АВ=АС, если
Решение:
Т.к. ОА┴(ОВС) ,то ОА ┴ ОВ. ?
По условию ОА=ОD, поэтому прямая ОВ является серединным перпендикуляром к отрезку АD, и , следовательно АВ= DB. ?
Теорема: Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
а)
б) Т.к. ОА ┴ (ОВС), то ОА┴ОС ? и ОА ┴ОВ. Если ОВ=ОС, то прямоугольные треугольники АОС и АОВ равны по двум катетам и следовательно, равны их гипотенузы, т.е. АВ=АС.
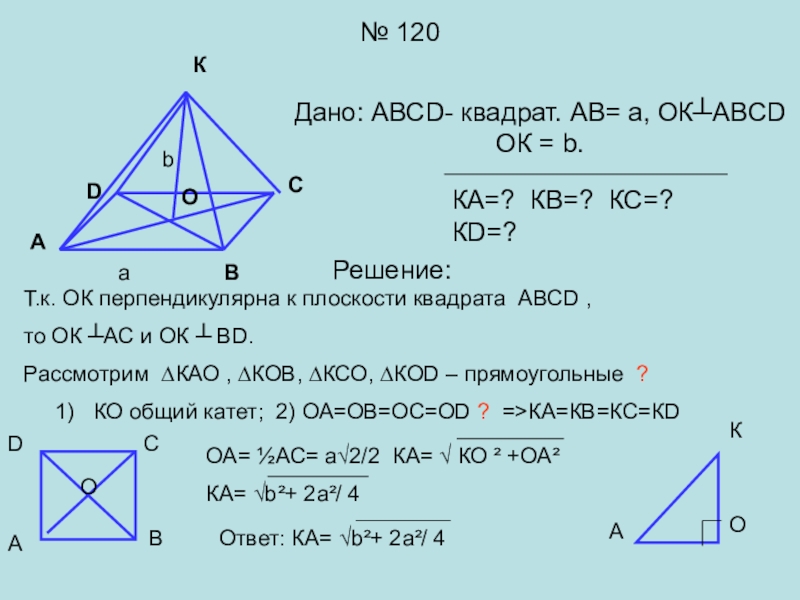
Слайд 14№ 120
Дано: АВСD- квадрат. АВ= а, ОК┴АВСD ОК = b.
А
В
С
D
К
О
а
b
КА=?
Решение:
Т.к. ОК перпендикулярна к плоскости квадрата АВСD ,
то ОК ┴АС и ОК ┴ ВD.
Рассмотрим ∆КАО , ∆КОВ, ∆КСО, ∆КОD – прямоугольные ?
КО общий катет; 2) ОА=ОВ=ОС=ОD ? =>КА=КВ=КС=КD
А
В
С
D
О
ОА= ½АС= а√2/2 КА= √ КО ² +ОА²
КА= √b²+ 2а²/ 4
А
О
К
Ответ: КА= √b²+ 2а²/ 4