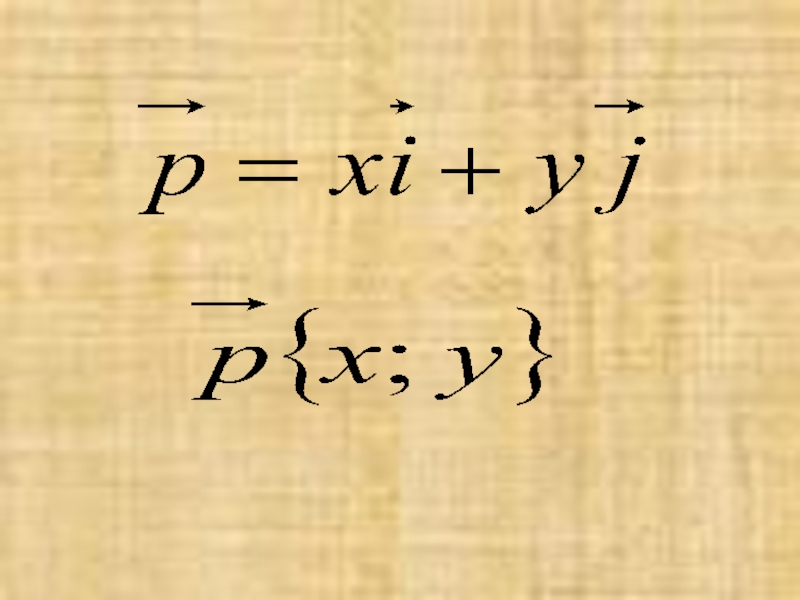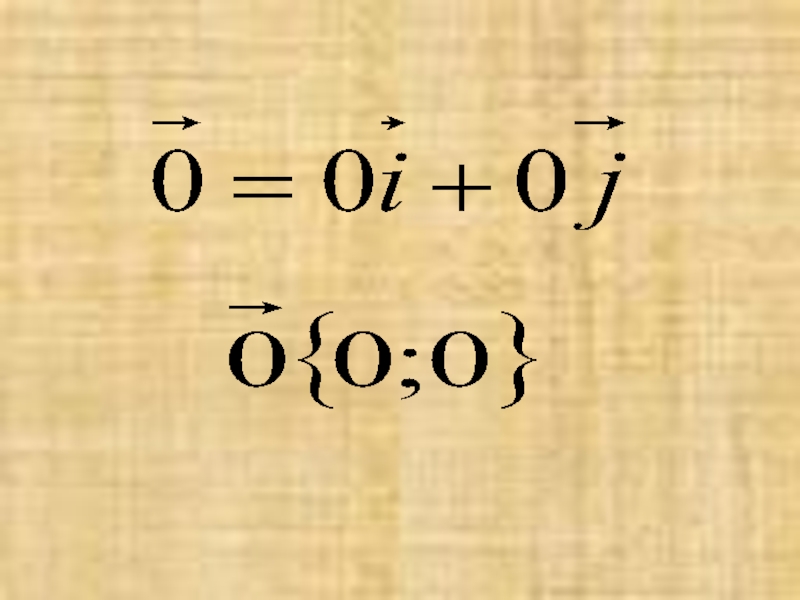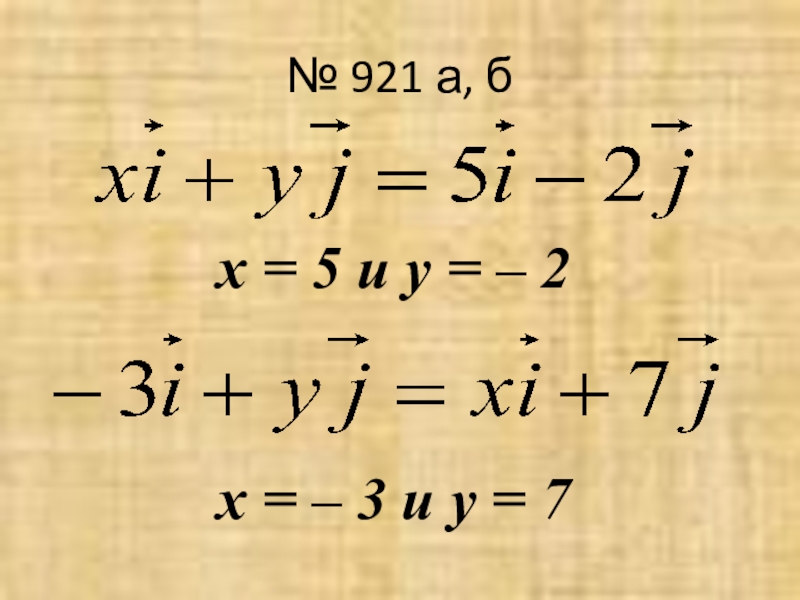- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Координаты вектора 9 класс
Содержание
- 1. Презентация по геометрии Координаты вектора 9 класс
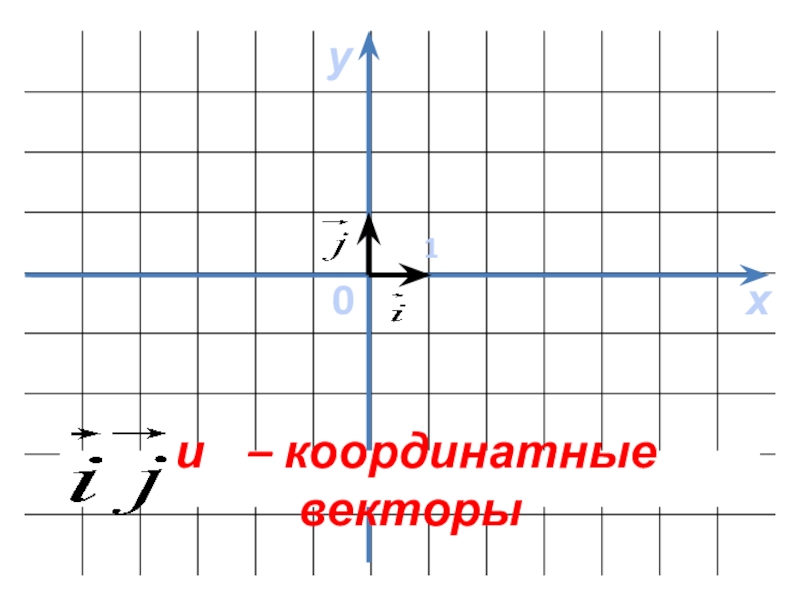
- 2. ху01
- 3. Слайд 3
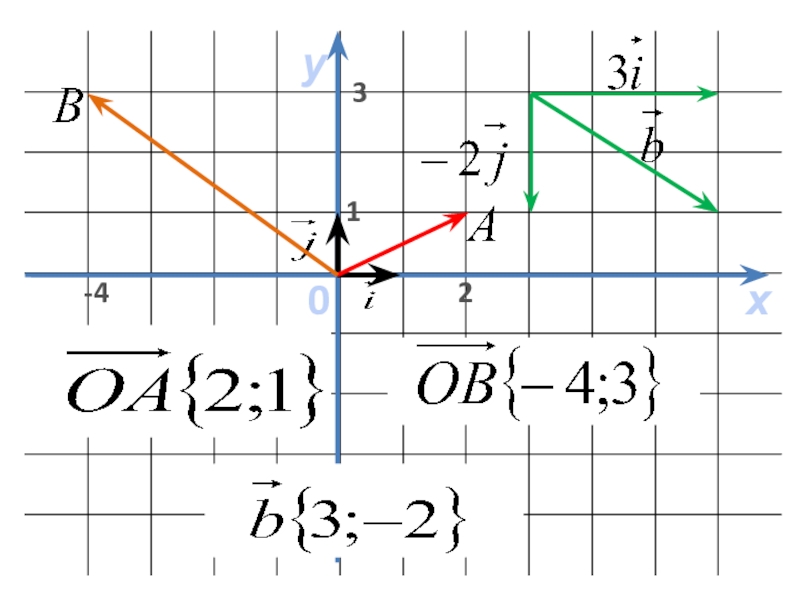
- 4. ху01-432
- 5. Слайд 5
- 6. Координаты равных векторов соответственно равны
- 7. 10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. и
- 8. 20. Каждая координата разности двух или более
- 9. Найдём координаты вектора
- 10. ху4 - 2 - 2 2 2
- 11. Даны векторы
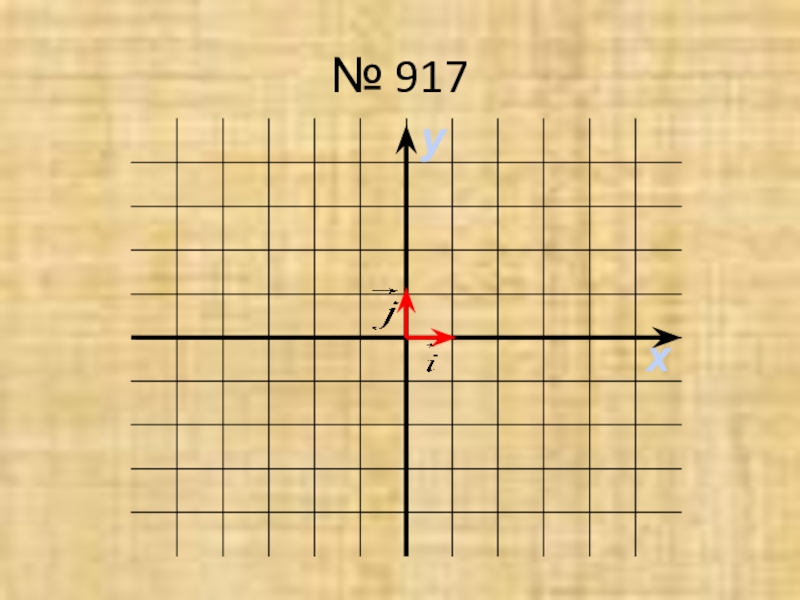
- 12. № 917ху
- 13. № 921 а, бх = 5 и
- 14. Слайд 14
- 15. Домашнее задание: п. 87, вопросы 7 – 8. № 918, 919,922(б,г).
ху01
Слайд 710. Каждая координата суммы двух или более векторов равна сумме соответствующих
координат этих векторов.
и
Слайд 820. Каждая координата разности двух или более векторов равна разности соответствующих
координат этих векторов.
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Слайд 10х
у
4
- 2
- 2
2
2
- 4
- 4
4
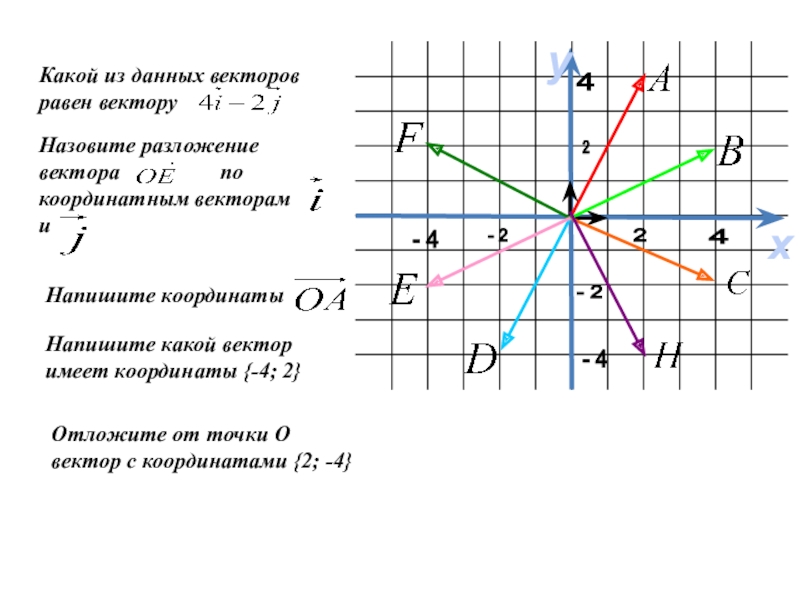
Какой из данных векторов равен вектору
Назовите разложение вектора по координатным векторам и
Напишите координаты
Напишите какой вектор имеет координаты {-4; 2}
Отложите от точки О вектор с координатами {2; -4}
Слайд 14 №922(а,в) а) а+в=(3+2;2+5)=(5;7) в)а+в=(-4+5;-2+3)=(1;1)
№923(а,в)
а)а-в=(5-2;3-1)=(3;2)
в)а-в=(3-4;6-(-3))=(-1;9)
