- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии для 10 класса по теме Параллельность прямых и плоскостей
Содержание
- 1. Презентация по геометрии для 10 класса по теме Параллельность прямых и плоскостей
- 2. 1) ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕПЛАН:2) ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ
- 3. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕВ ПРОСТРАНСТВЕ
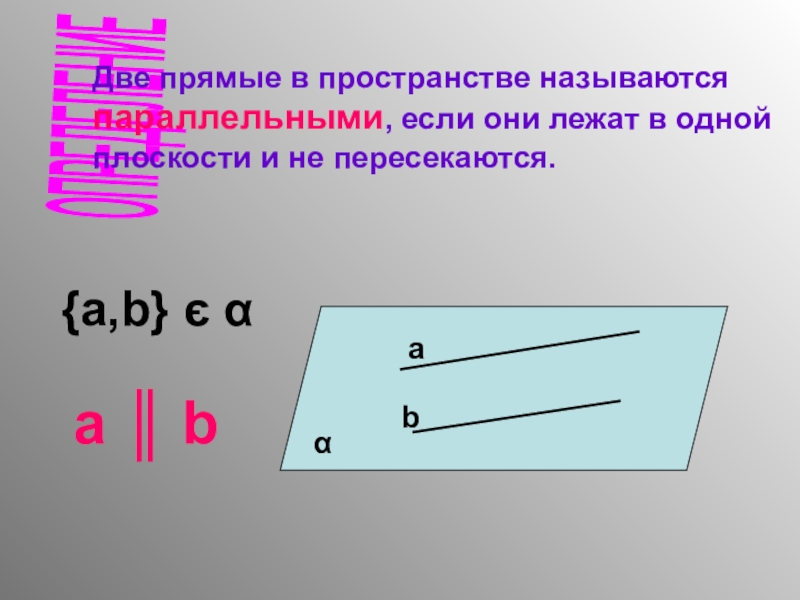
- 4. ОПРЕДЕЛЕНИЕ Две прямые в пространстве называются параллельными,
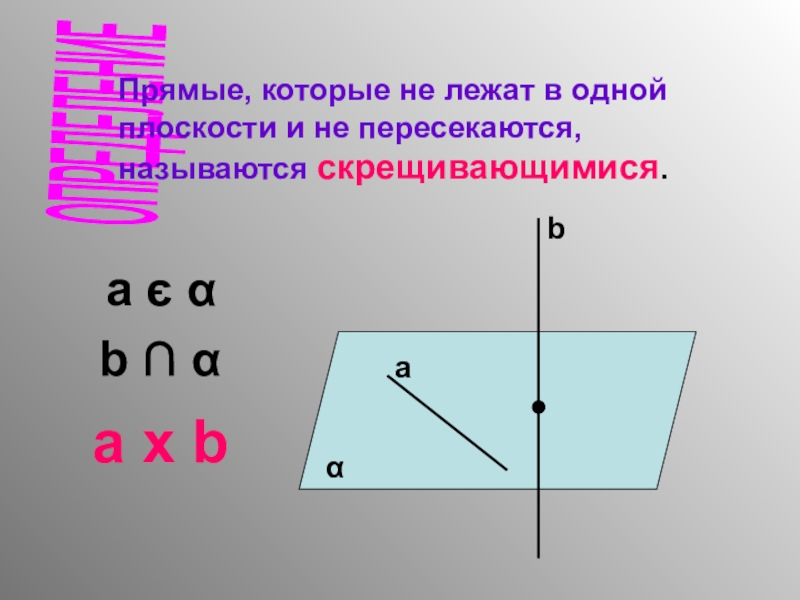
- 5. ОПРЕДЕЛЕНИЕ Прямые, которые не лежат в одной
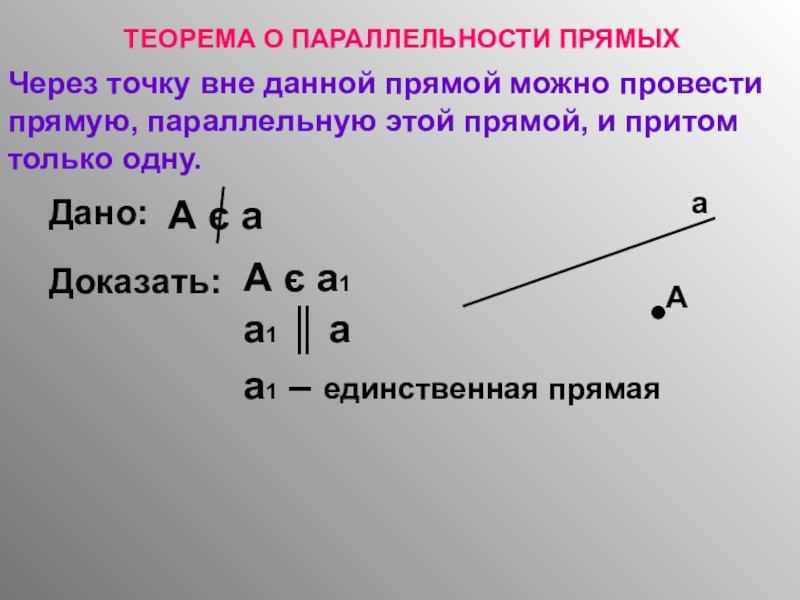
- 6. Через точку вне данной прямой можно провести
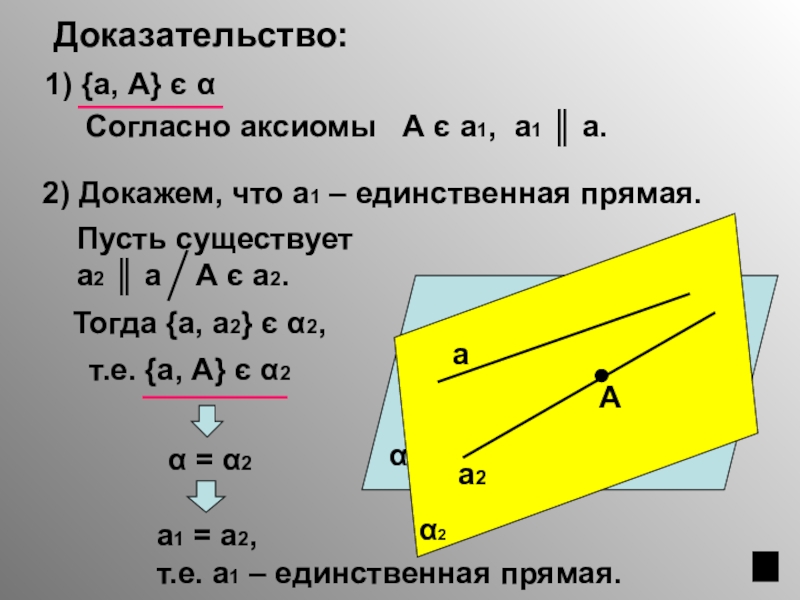
- 7. Доказательство:Аα1) {а, А} є αа12) Докажем, что
- 8. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕВ ПРОСТРАНСТВЕ
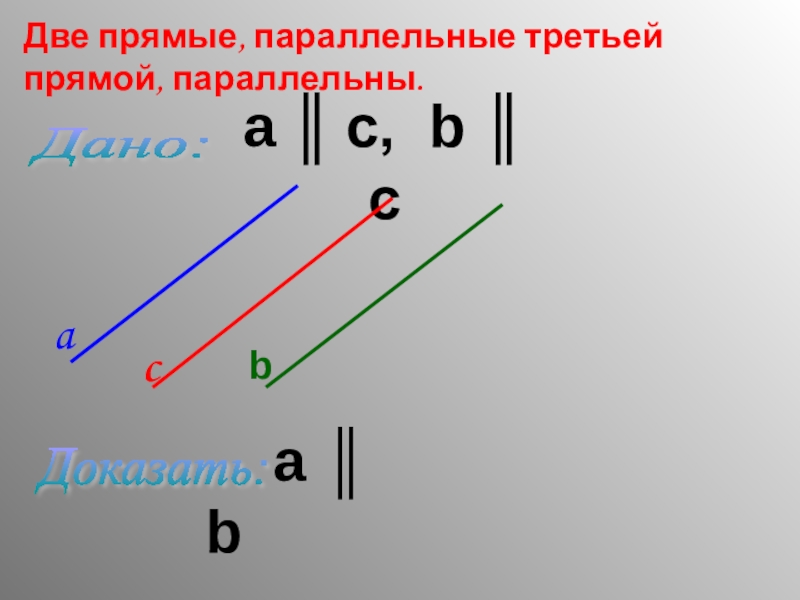
- 9. Дано: Доказать: Две прямые,
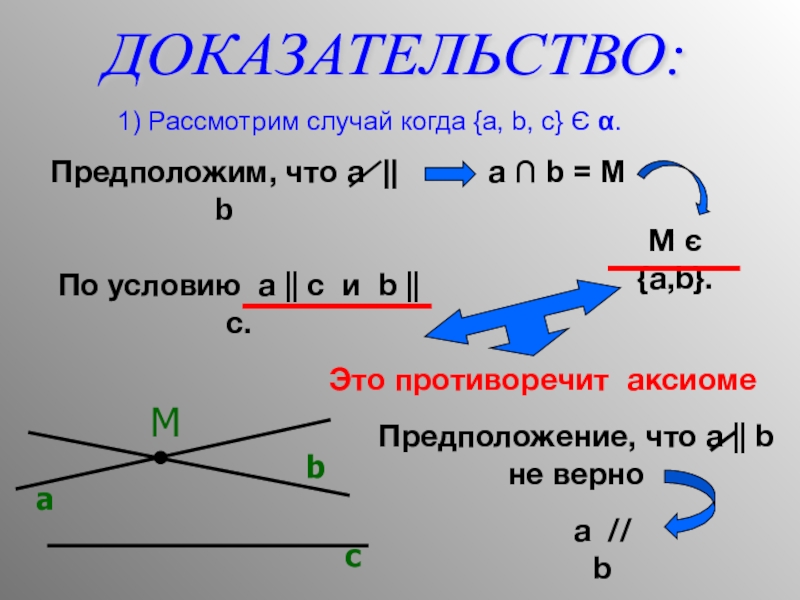
- 10. 1) Рассмотрим случай когда
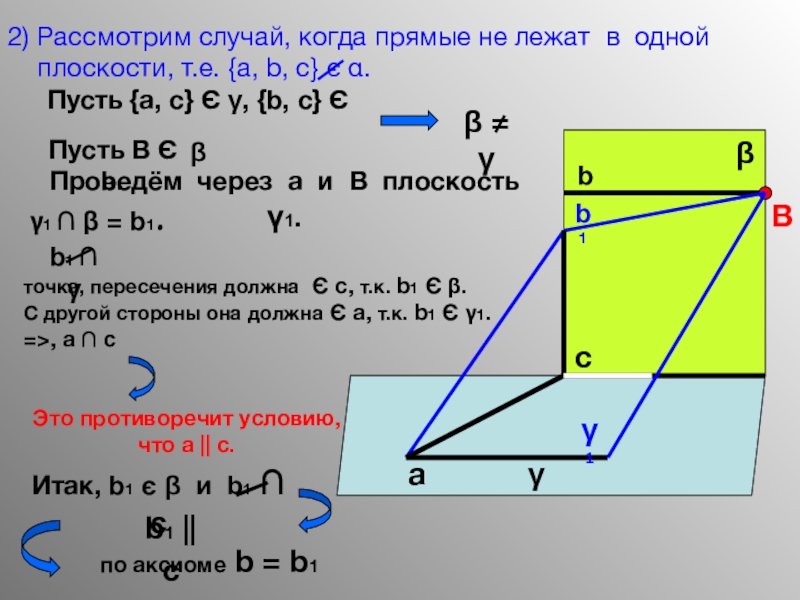
- 11. 2) Рассмотрим случай, когда прямые не лежат
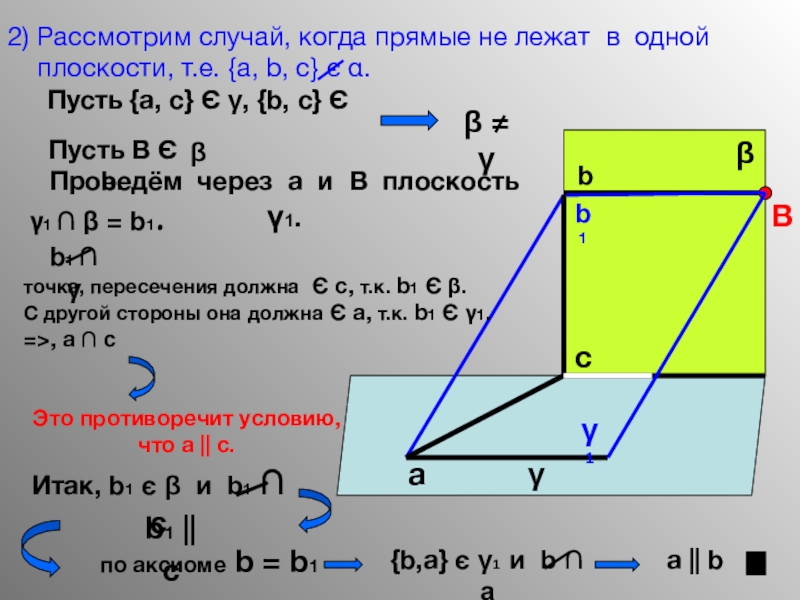
- 12. 2) Рассмотрим случай, когда прямые не лежат
- 13. №34 Какого взаимное расположение прямых?1) NД И
- 14. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИПРЯМОЙ И ПЛОСКОСТИ
- 15. Дано: Доказать: Если прямая,
- 16. Проведём через a и b плоскость β.abβαα
- 17. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИПЛОСКОСТЕЙ
- 18. Если две пересекающиеся прямые одной плоскости соответственно
- 19. Доказательство от противногоса ϵ α; а1 ϵ
- 20. СУЩЕСТВОВАНИЕПЛОСКОСТИ,ПАРАЛЛЕЛЬНОЙДАННОЙПЛОСКОСТИ
- 21. Через точку вне данной плоскости можно провести
- 22. αβДоп. построение а ϵ α; b ϵ
- 23. αβСМ ||bb1 || bМβ1γ ∩ α =
- 24. ПРОВЕРИМ ПАМЯТЬ
- 25. 1. ТОЧКИ А, В, С, Д
- 26. 2. Сторона АВ треугольника АВС принадлежит
- 27. 3. Через концы отрезка АВ, не пересекающего
- 28. 4. Плоскость α, параллельная стороне ВС треугольника
- 29. 5. Через концы отрезка АВ и точку
- 30. 6. Точки М, N, Р – параллельные
- 31. 7. Выберите верное продолжение фразы: проекция
- 32. 8. ТОЧКИ А, В, С, Д
- 33. 9. Сторона АД треугольника АВД принадлежит
- 34. СВОЙСТВАПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
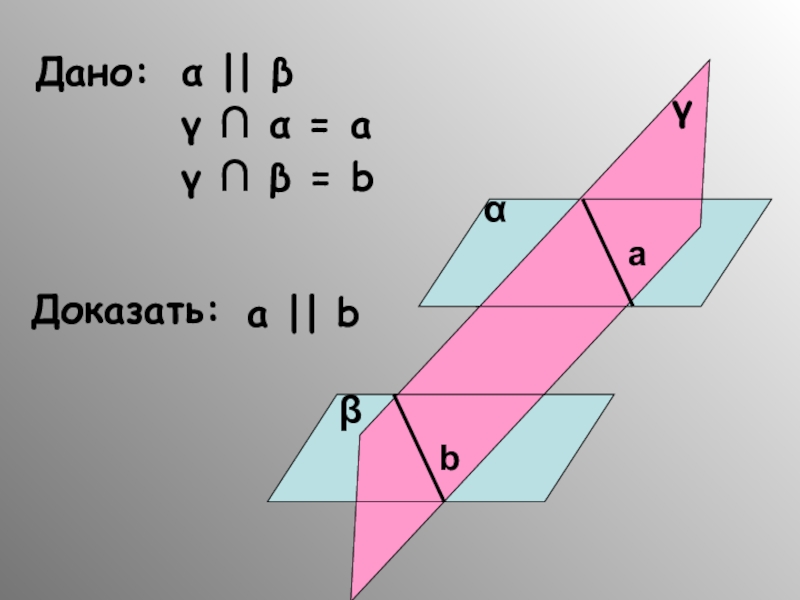
- 35. Свойство I: Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения параллельны.
- 36. Дано:α || β γ ∩ α = аγ ∩ β = bДоказать: a || bαβγab
- 37. Доказательство: 1) γ ∩ α = а
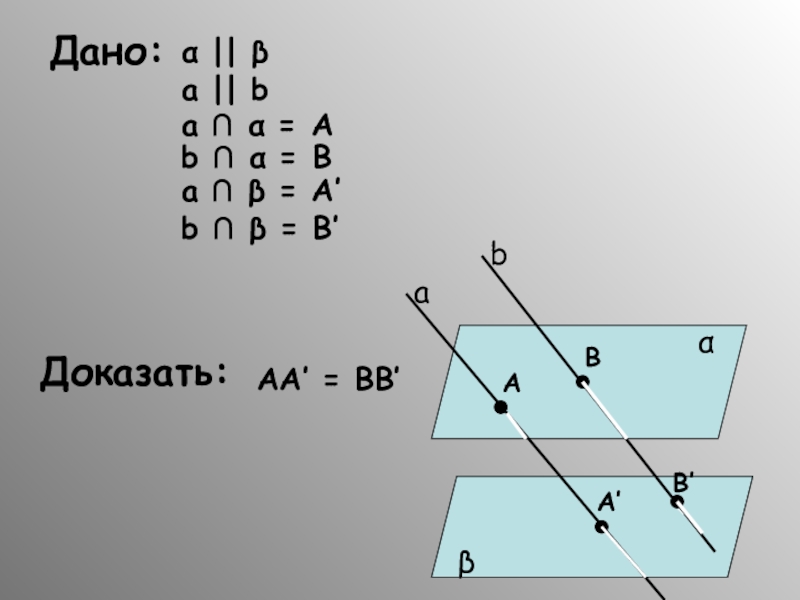
- 38. Свойство II: Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями равны.
- 39. Дано:α || βa || ba ∩ α
- 40. Доказательство:{ a, b } є γ (по
- 41. Отвечаем на вопросыМогут ли прямая и плоскость
- 42. Проверяем свою работуМогут ли прямая и плоскость
Слайд 21) ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ
ПЛАН:
2) ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
3) ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ
4) ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ
5) СУЩЕСТВОВАНИЕ ПЛОСКОСТИ, ПАРАЛЛЕЛЬНОЙ
ДАННОЙ ПЛОСКОСТИ
6) СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
Слайд 4ОПРЕДЕЛЕНИЕ
Две прямые в пространстве называются
параллельными, если они лежат в
плоскости и не пересекаются.
α
а
b
{а,b} є α
а ║ b
Слайд 5ОПРЕДЕЛЕНИЕ
Прямые, которые не лежат в одной
плоскости и не пересекаются,
называются скрещивающимися.
α
а
b
а є α
b ∩ α
a х b
Слайд 6Через точку вне данной прямой можно провести прямую, параллельную этой прямой,
Дано:
А є а
Доказать:
А є а1
а1 ║ а
а1 – единственная прямая
ТЕОРЕМА О ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
Слайд 7
Доказательство:
А
α
1) {а, А} є α
а1
2) Докажем, что а1 – единственная прямая.
Согласно
Пусть существует
а2 ║ а А є а2.
Тогда {а, а2} є α2,
т.е. {а, А} є α2
α = α2
а1 = а2,
т.е. а1 – единственная прямая.
а
а2
А
α2
Слайд 10
1) Рассмотрим случай когда {a, b, c} Є
ДОКАЗАТЕЛЬСТВО:
М
a
b
c
Предположим, что a || b
a ∩ b = М
М є {a,b}.
По условию a || c и b || c.
Это противоречит аксиоме
Предположение, что a || b
не верно
a // b
Слайд 112) Рассмотрим случай, когда прямые не лежат в одной
Пусть {a, с} Є γ, {b, c} Є β
β ≠ γ
Пусть B Є b.
Проведём через a и B плоскость γ1.
a
c
b
β
γ
В
γ1
γ1 ∩ β = b1.
b1
b1 ∩ γ
точка, пересечения должна Є c, т.к. b1 Є β.
С другой стороны она должна Є a, т.к. b1 Є γ1.
=>, a ∩ c
Это противоречит условию,
что а || c.
Итак, b1 є β и b1 ∩ c
b1 || c
по аксиоме b = b1
Слайд 122) Рассмотрим случай, когда прямые не лежат в одной
Пусть {a, с} Є γ, {b, c} Є β
β ≠ γ
Пусть B Є b.
Проведём через a и B плоскость γ1.
a
c
b
β
γ
В
γ1
γ1 ∩ β = b1.
b1
b1 ∩ γ
точка, пересечения должна Є c, т.к. b1 Є β.
С другой стороны она должна Є a, т.к. b1 Є γ1.
=>, a ∩ c
Это противоречит условию,
что а || c.
Итак, b1 є β и b1 ∩ c
b1 || c
по аксиоме b = b1
{b,a} є γ1 и b ∩ a
a || b
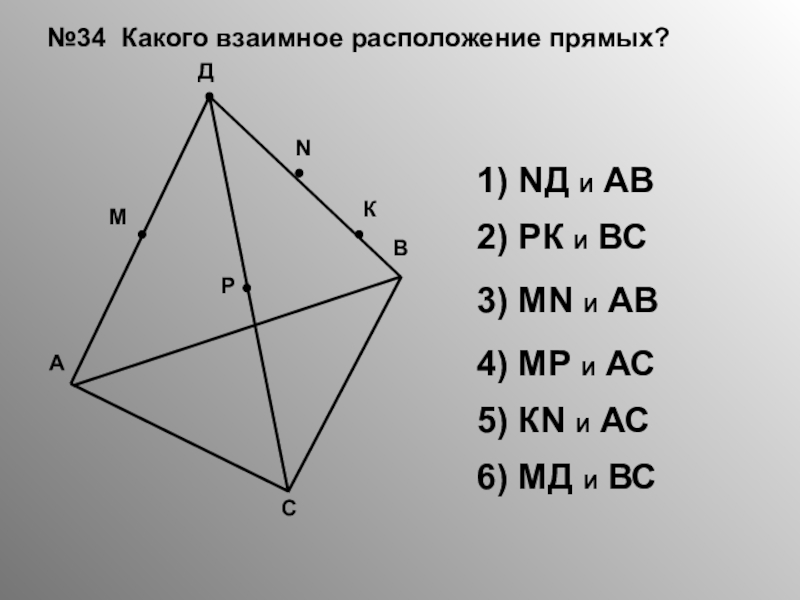
Слайд 13№34 Какого взаимное расположение прямых?
1) NД И АВ
2) РК И ВС
3)
4) МР И АС
5) КN И АС
6) МД И ВС
Слайд 15
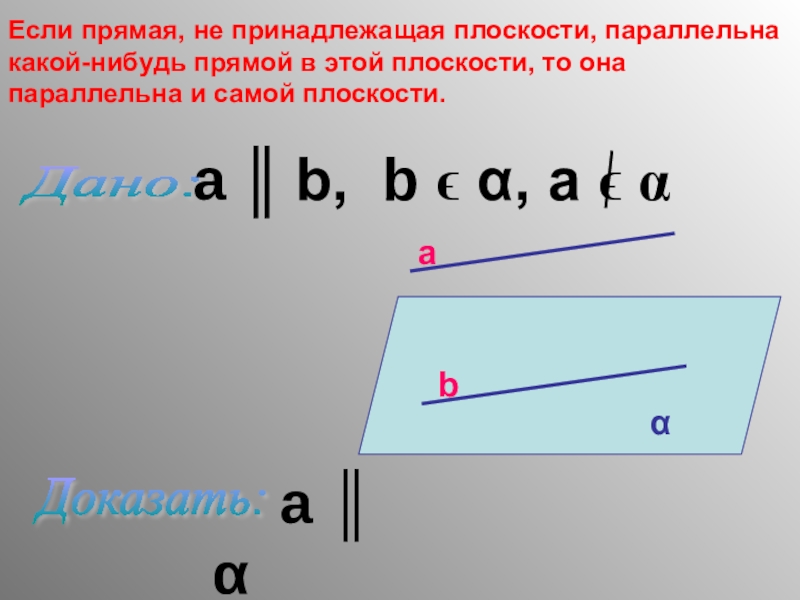
Дано:
Доказать:
Если прямая, не принадлежащая плоскости, параллельна
a ║ α
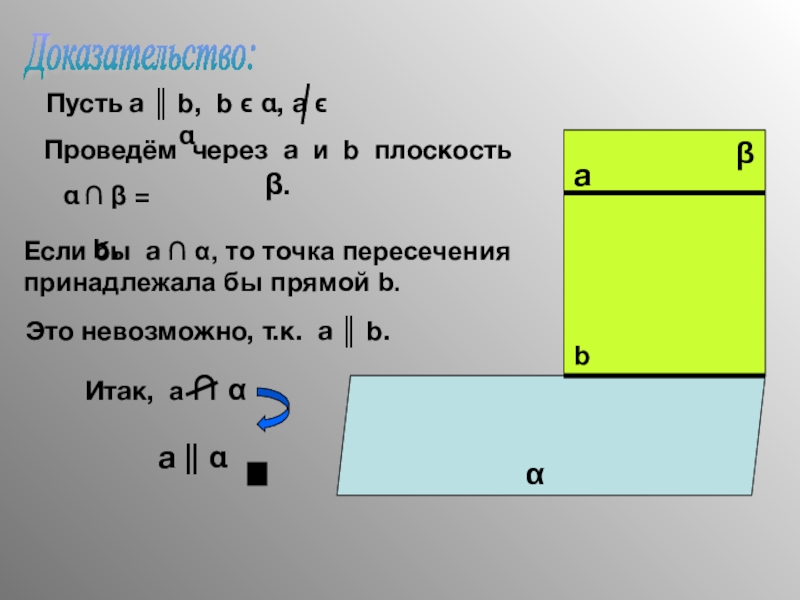
Слайд 16Проведём через a и b плоскость β.
a
b
β
α
α ∩ β = b.
Если
а || α
Доказательство:
Это невозможно, т.к. a ║ b.
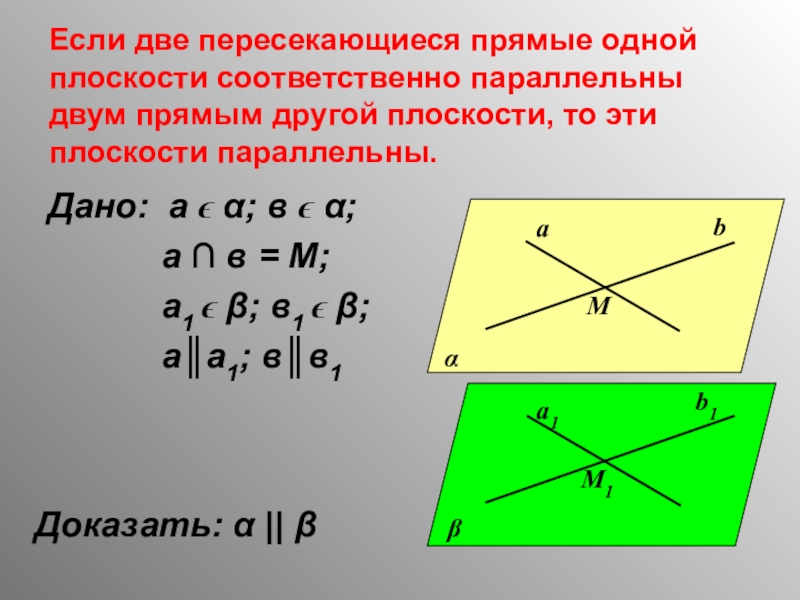
Слайд 18Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой
Дано: а ϵ α; в ϵ α;
а ∩ в = М;
а1 ϵ β; в1 ϵ β;
а║а1; в║в1
Доказать: α || β
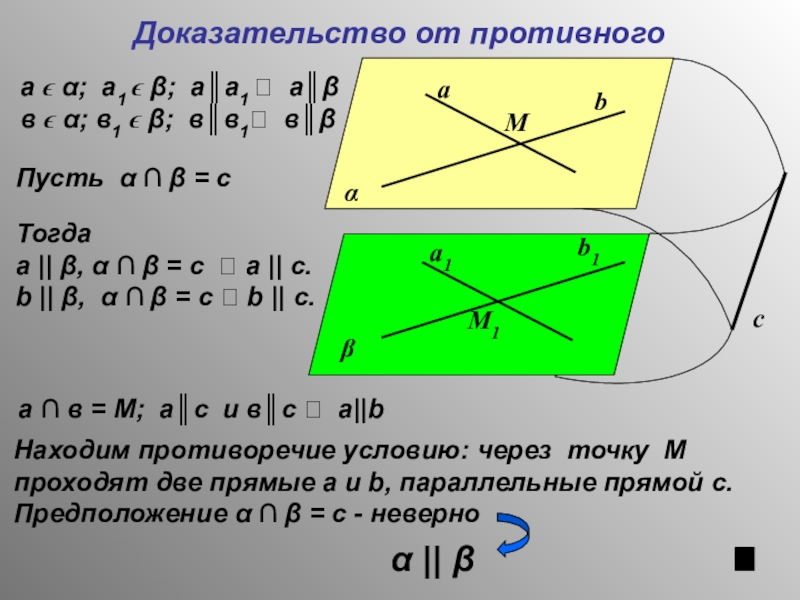
Слайд 19Доказательство от противного
с
а ϵ α; а1 ϵ β; а║а1 ? а║β
в
Пусть α ∩ β = с
Тогда
а || β, α ∩ β = с ? а || с.
b || β, α ∩ β = с ? b || с.
а ∩ в = М; а║с и в║с ? а||b
Находим противоречие условию: через точку М проходят две прямые а и b, параллельные прямой с.
Предположение α ∩ β = с - неверно
α || β
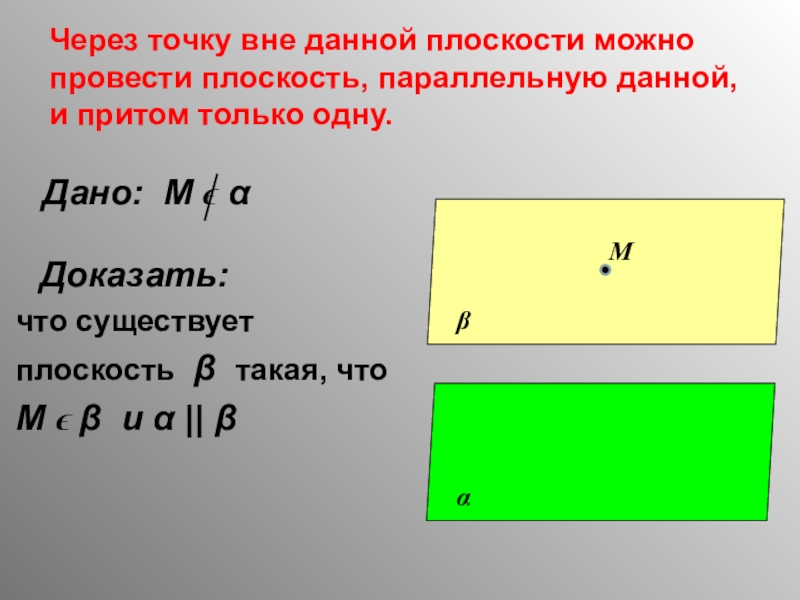
Слайд 21Через точку вне данной плоскости можно провести плоскость, параллельную данной, и
α
β
М
Доказать:
что существует
плоскость β такая, что
М ϵ β и α || β
Слайд 22
α
β
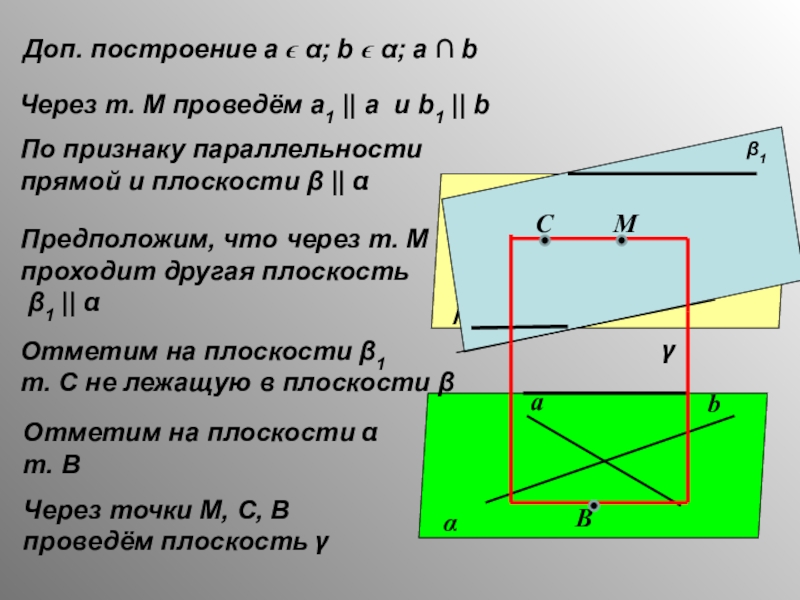
Доп. построение а ϵ α; b ϵ α; а ∩ b
Через
По признаку параллельности
прямой и плоскости β || α
Предположим, что через т. М проходит другая плоскость
β1 || α
М
β1
Отметим на плоскости β1
т. С не лежащую в плоскости β
С
В
Отметим на плоскости α
т. В
Через точки М, С, В проведём плоскость γ
γ
Слайд 23
α
β
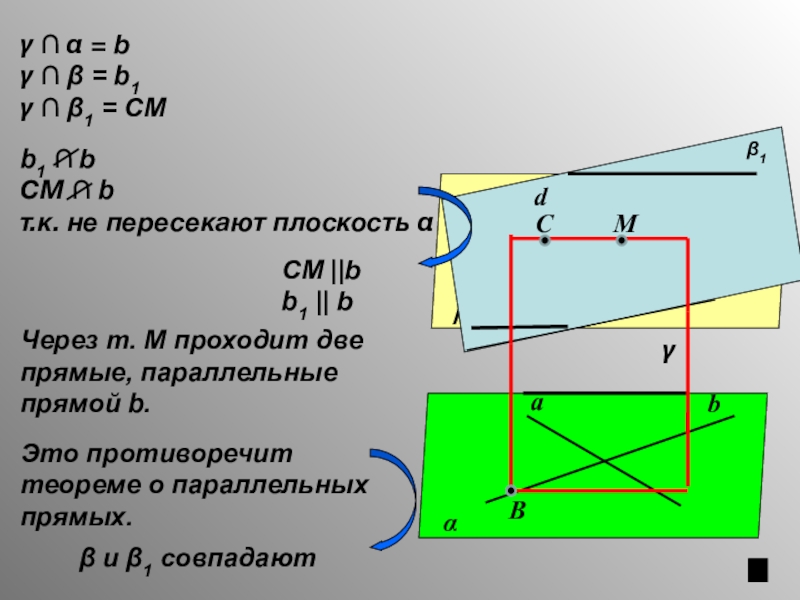
СМ ||b
b1 || b
М
β1
γ ∩ α = b
γ ∩ β =
γ ∩ β1 = CМ
С
В
Через т. М проходит две прямые, параллельные прямой b.
Это противоречит теореме о параллельных прямых.
γ
d
b1 ∩ b
СМ ∩ b
т.к. не пересекают плоскость α
β и β1 совпадают
Слайд 251. ТОЧКИ А, В, С, Д НЕ ЛЕЖАТ В ОДНОЙ
А) прямая АВ параллельна прямой СД
Б) прямая АВ пересекает прямую ВД
В) прямая АС пересекает прямую ВД
Г) прямые АС и ВД – скрещиваются.
Слайд 262. Сторона АВ треугольника АВС принадлежит
плоскости
АВ, - проекция точки С на плоскость α. Точка Т –
середина АВ. Выберите верное утверждение.
А) прямые СТ и АВ не пересекаются
Б) прямые СТ и АВ параллельны
В) прямые ВТ и АД пересекаются
Г) прямые АТ и ВД скрещивающиеся.
Слайд 273. Через концы отрезка АВ, не пересекающего плоскость
плоскость α в точках А1, В1 и С1 соответственно. Найдите длину отрезка СС1, если АА1 = 12см, а ВВ1 = 6см.
А) 6см
Б) 9см
В) см
Г) другой ответ
Слайд 284. Плоскость α, параллельная стороне ВС треугольника АВС, пересекает стороны АВ
А) 16см
Б) 4,8см
В) 12см
Г) другой ответ
Слайд 295. Через концы отрезка АВ и точку С этого отрезка проведены
А) 9,5см
Б) 7см
В) 8см
Г) другой ответ
Слайд 306. Точки М, N, Р – параллельные проекции точек
А) 21см
Б) 28см
В) 24см
Г) другой ответ
Слайд 317. Выберите верное продолжение фразы: проекция
трапеции на плоскость
проектировании может быть…
А) параллелограммом или трапецией
Б) только трапецией
В) отрезком или трапецией
Г) ромбом или трапецией.
Слайд 328. ТОЧКИ А, В, С, Д ЛЕЖАТ В ОДНОЙ
УТВЕРЖДЕНИЕ:
А) прямая ВС параллельна прямой АД
Б) прямая АС пересекает прямую ВД
В) прямая АД пересекает прямую ВС
Г) прямые АВ и СД – скрещиваются.
Слайд 339. Сторона АД треугольника АВД принадлежит
плоскости
АД, - проекция точки В на плоскость α. Точка F –
середина АВ. Выберите неверное утверждение.
А) прямые FД и АС пересекаются
Б) прямые FС и АД скрещиваются
В) прямые ВС и FC пересекаются
Г) прямые ВС и АД скрещивающиеся.
Слайд 35Свойство I:
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые
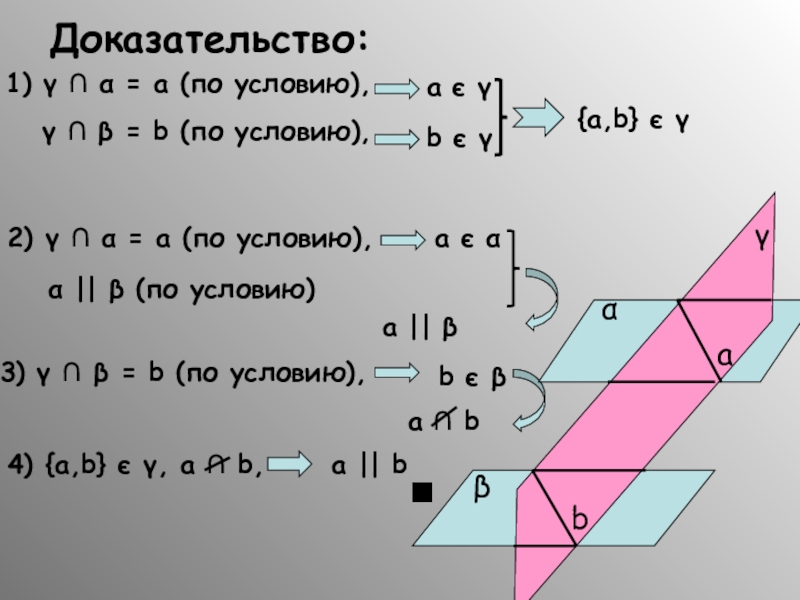
Слайд 37Доказательство:
1) γ ∩ α = а (по условию),
а є γ
{a,b} є γ
γ ∩ β = b (по условию),
b є γ
2) γ ∩ α = а (по условию),
a є α
α || β (по условию)
a || β
3) γ ∩ β = b (по условию),
b є β
a ∩ b
4) {a,b} є γ, a ∩ b,
a || b
α
β
a
b
γ
Слайд 38Свойство II:
Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями равны.
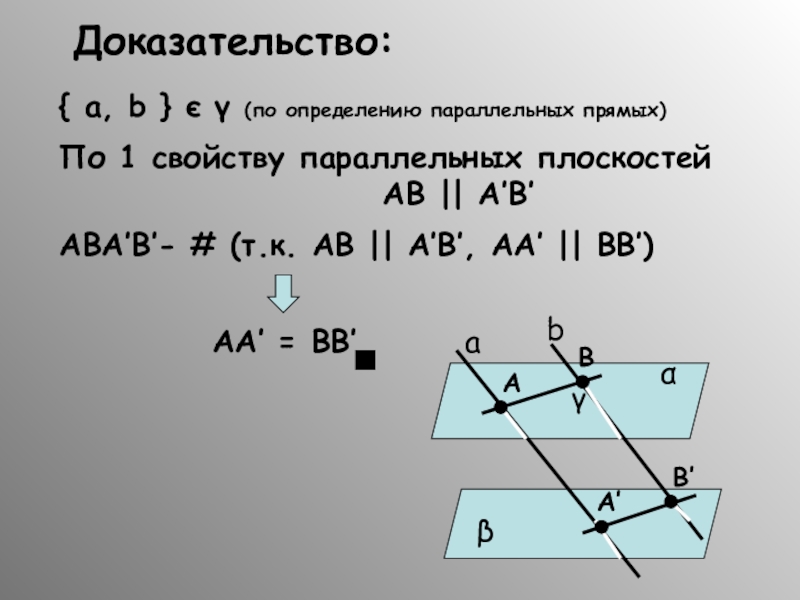
Слайд 40Доказательство:
{ a, b } є γ (по определению параллельных прямых)
По 1
AB || A’B’
ABA’B’- # (т.к. AB || A’B’, AA’ || BB’)
AA’ = BB’
α
β
a
b
γ
A
B
A’
B’
Слайд 41Отвечаем на вопросы
Могут ли прямая и плоскость не иметь общих точек?
Верно
Плоскости α и β параллельны, прямая m не лежит в плоскости α. Верно ли, что прямая m параллельна плоскости β?
Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку?
Боковые стороны трапеции параллельны плоскости α. Верно ли, что плоскость трапеции параллельна плоскости α?
Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции?
Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей?
Верно ли, что любые четыре точки лежат в одной плоскости?
Верно ли, что если две стороны треугольника параллельны плоскости α, то и третья сторона параллельна плоскости α?
Слайд 42Проверяем свою работу
Могут ли прямая и плоскость не иметь общих точек?
Верно ли, что если две прямые не пересекаются, то они параллельны? Нет
Плоскости α и β параллельны, прямая m не лежит в плоскости α. Верно ли, что прямая m параллельна плоскости β? Да
Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку? Нет
Боковые стороны трапеции параллельны плоскости α. Верно ли, что плоскость трапеции параллельна плоскости α? Да
Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции? Нет
Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости? Нет
Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей? Нет
Верно ли, что любые четыре точки лежат в одной плоскости? Нет
Верно ли, что если две стороны треугольника параллельны плоскости α, то и третья сторона параллельна плоскости α? Да