- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Возрастание и убывание функции
Содержание
- 1. Презентация по алгебре Возрастание и убывание функции
- 2. Возрастающая функцияФункция f(х) называется возрастающей на некотором
- 3. Убывающая функцияФункция f(х) называется убывающей на некотором
- 4. Возрастающие и убывающие функции называются монотонными функциями.
- 5. Способы исследования функций на монотонностьСпособ 1. По определению возрастающей (убывающей) функции.Способ 2. По графику функции.
- 6. Пример №1. По графику функции y=f(x) ответьте
- 7. Тема урока: «Возрастание и убывание функции»
- 8. Слайд 8
- 9. Гипотеза Если f/(x) > 0 на некотором
- 10. Достаточный признак возрастания(убывания) функции
- 11. №1. Непрерывная функция y=f(x) задана
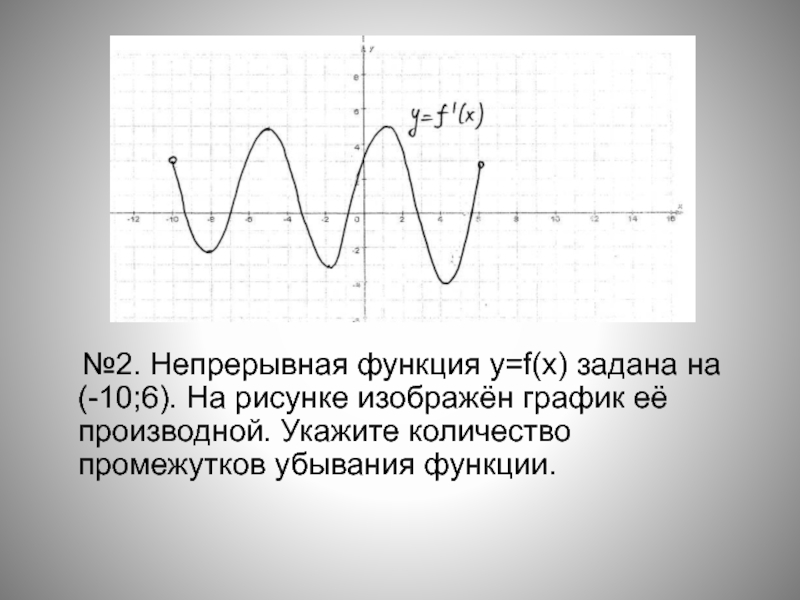
- 12. №2. Непрерывная функция y=f(x) задана
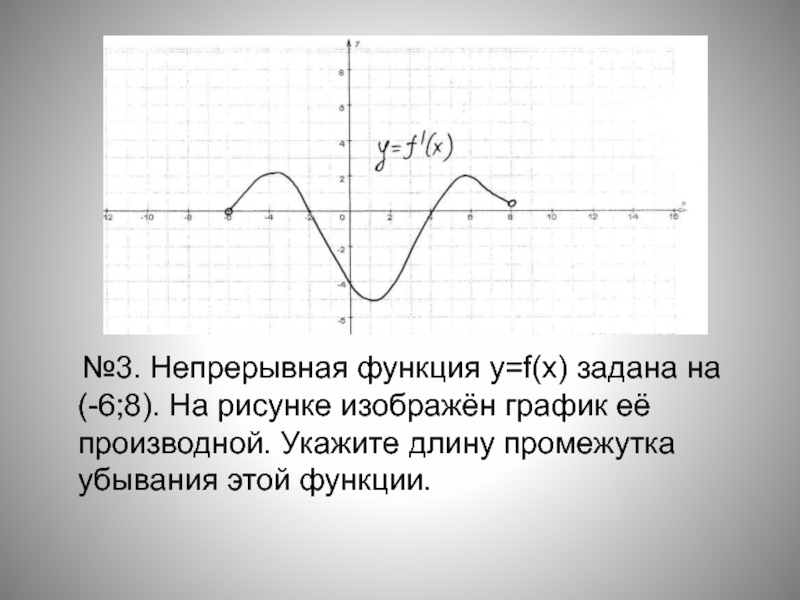
- 13. №3. Непрерывная функция y=f(x) задана
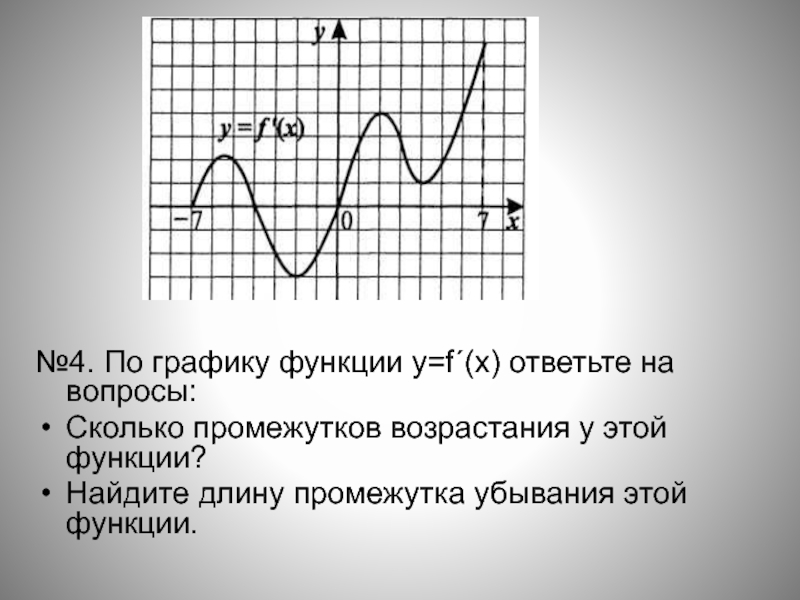
- 14. №4. По графику функции y=f´(x) ответьте на
- 15. Алгоритм 1. Указать область определения функции.
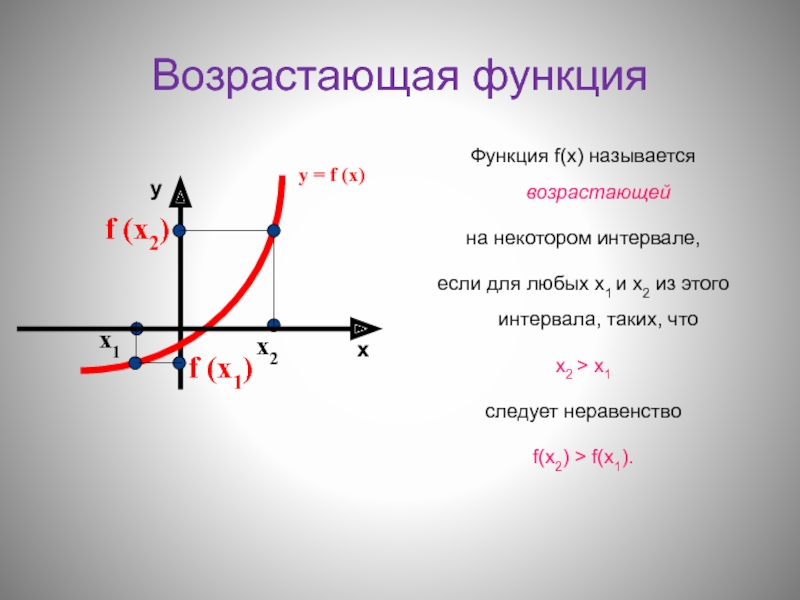
Возрастающая функцияФункция f(х) называется возрастающей на некотором интервале, если для любых х1 и х2 из этого интервала, таких, что х2 > х1 следует неравенство
Слайд 2Возрастающая функция
Функция f(х) называется возрастающей
на некотором интервале,
если для любых
х1 и х2 из этого интервала, таких, что
х2 > х1
следует неравенство
f(х2) > f(х1).
х2 > х1
следует неравенство
f(х2) > f(х1).
х
х1
х2
у
f (х1)
f (х2)
у = f (х)
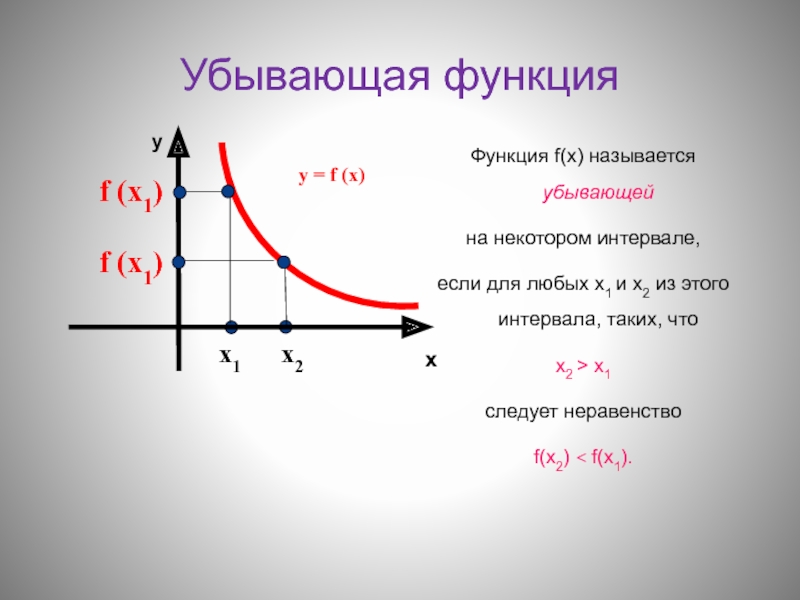
Слайд 3Убывающая функция
Функция f(х) называется убывающей
на некотором интервале,
если для любых
х1 и х2 из этого интервала, таких, что
х2 > х1
следует неравенство
f(х2) < f(х1).
х2 > х1
следует неравенство
f(х2) < f(х1).
х
х1
х2
f (х1)
f (х1)
у = f (х)
у
Слайд 5Способы исследования функций на монотонность
Способ 1. По определению возрастающей (убывающей) функции.
Способ
2. По графику функции.
Слайд 6
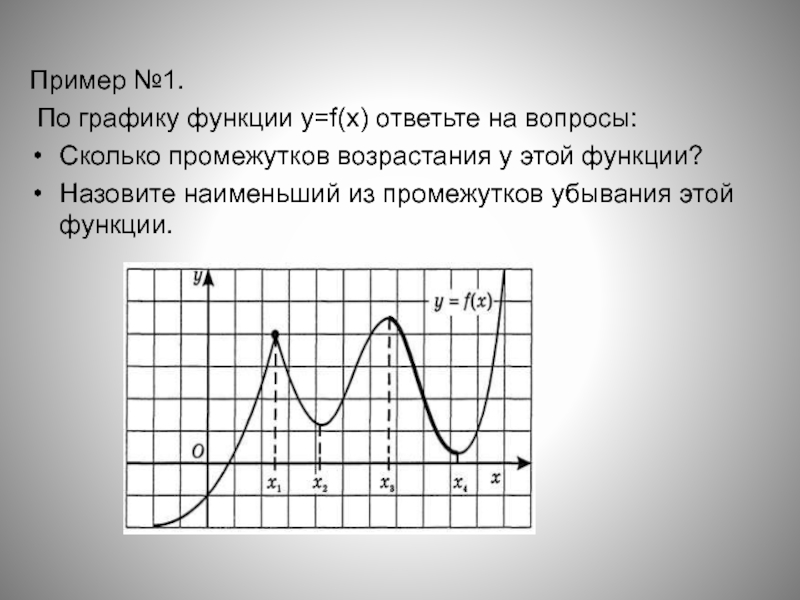
Пример №1.
По графику функции y=f(x) ответьте на вопросы:
Сколько промежутков возрастания
у этой функции?
Назовите наименьший из промежутков убывания этой функции.
Назовите наименьший из промежутков убывания этой функции.
Слайд 9Гипотеза
Если f/(x) > 0 на некотором интервале, то функция возрастает
на этом интервале.
Если f/(x) < 0 на некотором интервале, то функция убывает на этом интервале.
Если f/(x) < 0 на некотором интервале, то функция убывает на этом интервале.
Слайд 11
№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке
изображён график её производной. Укажите количество промежутков возрастания функции.
![№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество](/img/thumbs/2f4925115ce3fb18d7d170c7b4d20cef-800x.jpg "Презентация по алгебре Возрастание и убывание функции №1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён")
Слайд 12 №2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке
изображён график её производной. Укажите количество промежутков убывания функции.
Слайд 13 №3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке
изображён график её производной. Укажите длину промежутка убывания этой функции.
Слайд 14
№4. По графику функции y=f´(x) ответьте на вопросы:
Сколько промежутков возрастания у
этой функции?
Найдите длину промежутка убывания этой функции.
Найдите длину промежутка убывания этой функции.
Слайд 15Алгоритм
1. Указать область определения функции.
2. Найти производную
функции.
3. Определить промежутки, в которых
f/(x) > 0 и f/(x) < 0.
4. Сделать выводы о монотонности
функции.
3. Определить промежутки, в которых
f/(x) > 0 и f/(x) < 0.
4. Сделать выводы о монотонности
функции.
