СШ №1
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Теория вероятности в жизни
Содержание
- 1. Презентация по алгебре Теория вероятности в жизни
- 2. Цель:изучить особенности теории вероятностей, её значение и применение в повседневной жизни.
- 3. Задачи: Изучить историю и развитие теории вероятностейПроделать
- 4. Случайности и математикаСо случаем и случайностями мы
- 5. История и развитие теории вероятностейЕщё древние люди
- 6. Первые работы, в которых зарождались основные понятия
- 7. Подбрасывание монетыНапример, простой опыт – подбрасывание монеты.
- 8. Теория. Определения.Испытание – всякое действие, явление, наблюдение
- 9. История простейшего опытаКто и когда впервые проделал
- 10. Наблюдения показывают:Проделав подобный опыт, при подбрасывании монеты
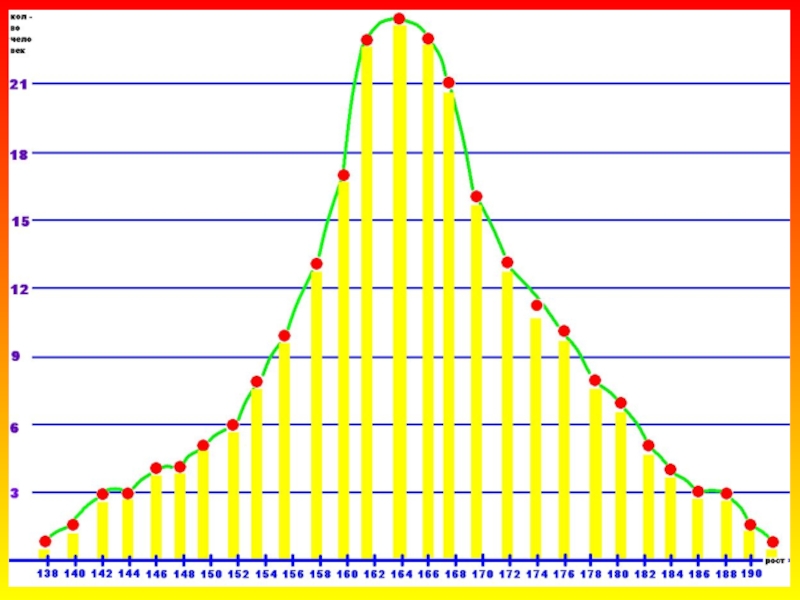
- 11. По результатам опроса, о росте женщин, получился следующий график
- 12. Слайд 12
- 13. На графике видно, что большинство – имеют
- 14. Исследование МуавраПодобную работу проводил французский математик А.Муавр
- 15. Закон «нормального» распределения имеет важное практическое значение.
- 16. Сколько времени ждать автобус?Каждому из нас не
- 17. Пусть АВ – промежуток между двумя появлениями
- 18. Методы теории вероятностей широко применяются в отраслях
- 19. Теория вероятностей помогает и имеет большое значение:В
- 20. В последние годы методы теории вероятностей всё
Цель:изучить особенности теории вероятностей, её значение и применение в повседневной жизни.
Слайд 1Презентация к уроку: «Теория вероятности»
Учитель: Димухаметова Людмила Александровна
г. Енисейск МАОУ
Слайд 3Задачи:
Изучить историю и развитие теории вероятностей
Проделать эксперименты
Провести исследование-наблюдение.
На основании изученного, сделать
выводы о значении теории вероятностей в нашей жизни.
Слайд 4Случайности и математика
Со случаем и случайностями мы встречаемся каждый день. Казалось
бы, что здесь не может быть никаких законов и формул, никакой математики, но это не так. В теории вероятностей существуют интереснейшие закономерности.
Слайд 5История и развитие теории вероятностей
Ещё древние люди знали и понимали, что
у 10 охотников «вероятность» поразить копьём зубра гораздо больше, чем у чем у одного, поэтому и охотились они коллективно.
Позднее, с опытом, человек всё чаще стал изучать случайные события, классифицировать их исходы как невозможные, возможные и достоверные.
Люди заметили, что случайностями очень часто управляют объективные закономерности.
Позднее, с опытом, человек всё чаще стал изучать случайные события, классифицировать их исходы как невозможные, возможные и достоверные.
Люди заметили, что случайностями очень часто управляют объективные закономерности.
Слайд 6Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой
попытки создания теории азартных игр. (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI – XVII вв.)
Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654-1705). Доказанная им теория получила в последствии название: «Закон больших чисел»
Основы теории вероятностей были изложены последовательно французским математиком П. Лапласом (1749-1827) в книге «Аналитическая теория вероятностей». Он отмечал, что важнейшие жизненные вопросы по большей части являются лишь задачами по теории вероятностей.
Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654-1705). Доказанная им теория получила в последствии название: «Закон больших чисел»
Основы теории вероятностей были изложены последовательно французским математиком П. Лапласом (1749-1827) в книге «Аналитическая теория вероятностей». Он отмечал, что важнейшие жизненные вопросы по большей части являются лишь задачами по теории вероятностей.
Слайд 7Подбрасывание монеты
Например, простой опыт – подбрасывание монеты. Выпадение герба или цифры
– конечно, случайное явление, но при многократном подбрасывании обычной монеты можно заметить, что появление герба/цифры происходит примерно в половине случаев.
Значит, можно сделать вывод, что результаты бросаний монеты, при неоднократном повторении подчиняются определённому закону, хотя каждое из них является случайным событием.
Значит, можно сделать вывод, что результаты бросаний монеты, при неоднократном повторении подчиняются определённому закону, хотя каждое из них является случайным событием.
Слайд 8Теория. Определения.
Испытание – всякое действие, явление, наблюдение с несколькими различными исходами,
реализуемое при данном комплексе условий.
Случайное событие – результат действия, возможный исход рассматриваемой ситуации.
Искомое событие (искомый исход) – интересующее нас какое-либо определённое событие.
Классическое определение вероятности события: Если при каких-либо условиях имеются r равновероятных событий, s из которых приводят к событию А, то вероятность Р{А} = s/r
Случайное событие – результат действия, возможный исход рассматриваемой ситуации.
Искомое событие (искомый исход) – интересующее нас какое-либо определённое событие.
Классическое определение вероятности события: Если при каких-либо условиях имеются r равновероятных событий, s из которых приводят к событию А, то вероятность Р{А} = s/r
Слайд 9История простейшего опыта
Кто и когда впервые проделал опыт с монетой, неизвестно.
Естествоиспытатель Ж. Л. Л. Бюффон в 18 веке 4040 раз подбрасывал монету – герб выпал 2048 раз. Математик К. Пирсон в начале 20 века подбрасывал её 24000 раз - герб выпал 12012 раз. Лет 50 назад американские экспериментаторы повторили опыт. При 10000 подбрасываниях герб выпал 4979 раз.
Слайд 10Наблюдения показывают:
Проделав подобный опыт, при подбрасывании монеты 1200 раз, выпал 597
раз герб и 603 раза – цифру, ещё раз убедившись, что выпадения орла и «решки» – события равновозможные, происходят примерно в соотношении 1:1.
Слайд 13 На графике видно, что большинство – имеют рост примерно 164 см,
другими словами, 164 см – это средний рост женщин нашего города, а если выразиться научным языком, 164 см – наиболее вероятный рост. Построенный график – колоколообразная кривая, кривая «нормального» распределения.
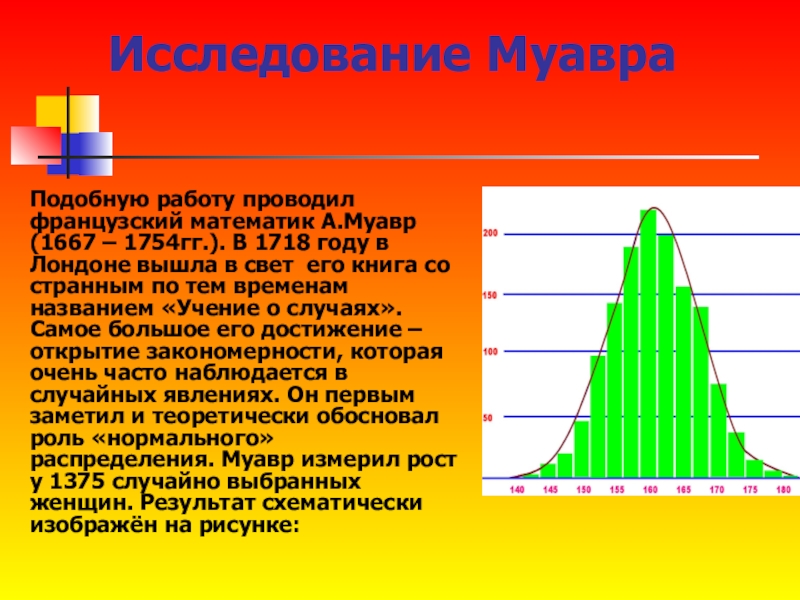
Слайд 14Исследование Муавра
Подобную работу проводил французский математик А.Муавр (1667 – 1754гг.). В
1718 году в Лондоне вышла в свет его книга со странным по тем временам названием «Учение о случаях». Самое большое его достижение – открытие закономерности, которая очень часто наблюдается в случайных явлениях. Он первым заметил и теоретически обосновал роль «нормального» распределения. Муавр измерил рост у 1375 случайно выбранных женщин. Результат схематически изображён на рисунке:
Слайд 15Закон «нормального» распределения имеет важное практическое значение. Оказывается, что так распределяется
скорость газовых молекул, вес новорождённых и много других случайных событий.
Слайд 16Сколько времени ждать автобус?
Каждому из нас не раз приходилось ездить на
автобусе. Поэтому, я решила разобрать интересную ситуацию: я пришла на остановку, интервал движения автобуса равен 40 минут. Расписания я не знаю. Ожидание, конечно, продлится не больше 40 минут. Найдём вероятность того, что автобус придёт не позже, чем через 10 минут.
Слайд 17Пусть АВ – промежуток между двумя появлениями автобуса. Момент моего прихода
на остановку обозначим точкой С на отрезке АВ. АС – время ожидания автобуса. Момент прихода автобуса случаен. Если разделить отрезок АВ точками D, E и F на четыре равные части, то можно считать равновероятными попадания точки С в каждую из четырёх частей. Тогда P {[t 10 минут]}=1/4
Слайд 18Методы теории вероятностей широко применяются в отраслях естествознания и техники: в
теории надёжности, массового обслуживания, стрельбы, ошибок наблюдений, автоматического управления, в общей теории связи , в теоретической физике, геодезии, астрономии и во многих других науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, анализе технологических процессов, предупредительном и приёмочном контроле качества продукции и для многих других целей.
Слайд 19Теория вероятностей помогает и имеет большое значение:
В промышленности и экономике. (Например,
при производстве одежды необходимо знать те размеры, которые наиболее вероятны. Когда будет производиться больше одежды нужного размера, тогда она будет лучше и быстрее реализовываться и, прибыль будет максимальной)
В юриспруденции. (Следователь или детектив в своей работе, путём логических рассуждений, устанавливает наиболее вероятную картину события)
В юриспруденции. (Следователь или детектив в своей работе, путём логических рассуждений, устанавливает наиболее вероятную картину события)
Слайд 20В последние годы методы теории вероятностей всё шире и шире проникают
в различные области науки и техники, способствуя их прогрессу. Теория вероятностей имеет большое значение для нас, мы очень часто сталкиваемся с ней в повседневной жизни.