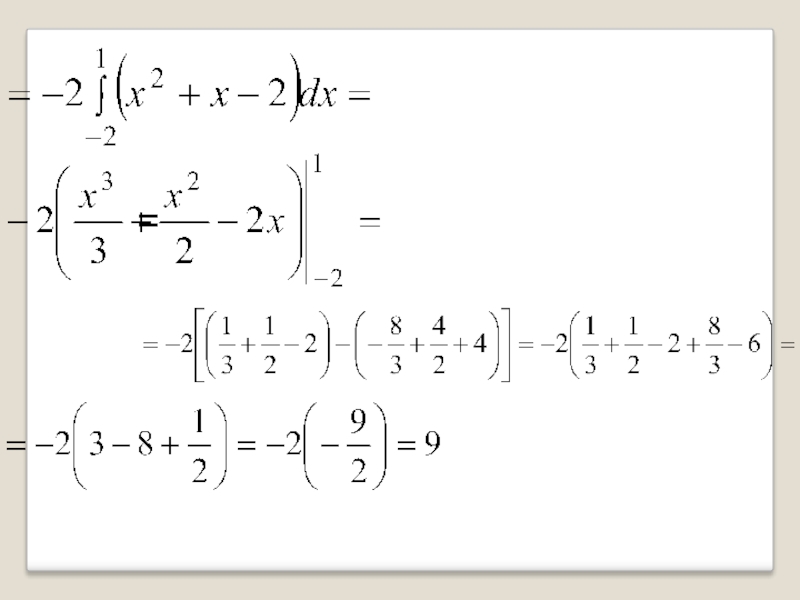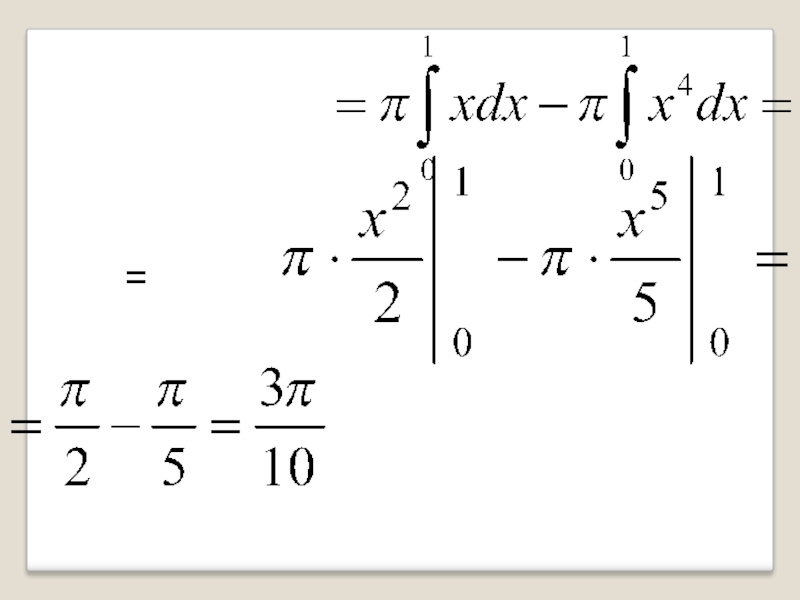- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре по теме: Первообразная и интеграл (11 класс)
Содержание
- 1. Презентация по алгебре по теме: Первообразная и интеграл (11 класс)
- 2. СодержаниеПервообразнаяИнтеграла) неопределённыйб) определённый
- 3. Первообразная
- 4. ОпределениеФункция F(х) называется первообразной функции f(х) на
- 5. Теорема 1Если функция f(х) непрерывна при
- 6. Теорема 2Если F(x) одна из первообразных функции
- 7. Таблица первообразных Зная формулы для нахождения производных, можно составить таблицу для нахождения первообразных
- 8. Правила нахождения первообразныхПервообразная суммы равна сумме первообразныхЕсли
- 9. Найдём одну из первообразныхЕсли f(x) равно:1) f(x)=2х+х³2) f(x)=4х-23) f(x)=х³-3х²+х-14) f(x)=4х⁵+2х+е5) f(x)=х⁴+3х²+56) f(x)=5cosx-3sin2xЗначит F(x) равно:F(x)= х²+х⁴⁄4F(x)=2х²-2хF(x)=х⁴⁄4-2х³+х²⁄2-хF(x)=2х⁶⁄3+х²+ехF(x)=х⁵⁄5+х³+5хF(x)=5sinx+3/2cosx
- 10. Ответить на вопрос: какая функция является
- 11. Выберите ответ, при котором предложение будет верно.
- 12. Ответить на вопрос: для какой
- 13. Ответить на вопрос: производная какой из функций
- 14. Задание №1. Найдите первообразную функции f(x), график
- 15. б) f(x)=3х - 5, А(4;10) Решение. F(x)=
- 16. СамостоятельноНайдите первообразную функции f(x), график которой проходит
- 17. Проверим ответы1) F(x)= х³⁄3 - 5х +
- 18. Задание №2. Найдите первообразную функции f(x), значение
- 19. б) f(x)=2sin3x+4cos(x/2); х₀=π⁄3; у₀=0Решение. F(x)=-2·1/3·cos3x+4·2
- 20. в) f(x)=4+6х²; х₀=2; у₀
- 21. г) f(x)=2х³+х²+3; х₀=1; у₀>0 Решение. F(x)=
- 22. Задание №3. Найдите множество первообразных функции f(x).
- 23. б) f(x) = sin5x·cos6x Решение. т.к.
- 24. Работаем по задачникустр. №
- 25. ИНТЕГРАЛЫ
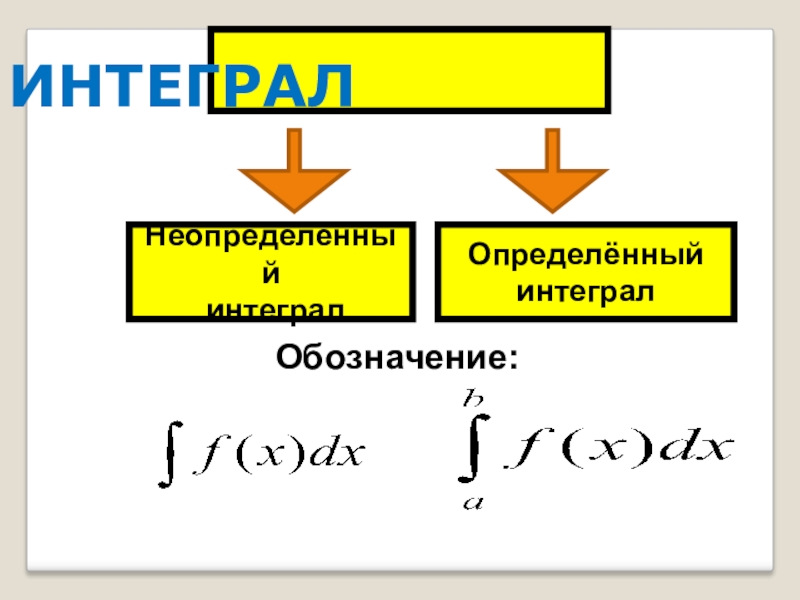
- 26. ИНТЕГРАЛНеопределённый интегралОпределённый интегралОбозначение:
- 27. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- 28. Определение:Множество всех первообразных функции f(x) на некотором
- 29. Основные свойства неопределенного интеграла. т.е. постоянный множитель можно выносить за знак интеграла
- 30. Основные свойства неопределенного интеграла.
- 31. Таблица основных неопределённых интегралов
- 32. Слайд 32
- 33. Таблица интегралов
- 34. ОпределениеПроцесс нахождения интеграла называется интегрированием.Интегрирование является операцией, обратной дифференцированию
- 35. Историческая справкаИнтегрирование прослеживается еще в древнем Египте,
- 36. Историческая справка метод исчерпывания Евдокса (примерно
- 37. Историческая справка Этот метод был подхвачен
- 38. Историческая справка Аналогичные методы были разработаны не
- 39. Историческая справкаЭтот метод впоследствии использовали Цзу Чунжи и Цзу Гэн для нахождения объема шара
- 40. Историческая справкаСледующий крупный шаг в исследование интегралов
- 41. Историческая справкаРешая эту проблему, он проводит вычисления,
- 42. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- 43. Определение Пусть функция y=f(x) определена и интегрируема
- 44. Определение Криволинейной трапецией называется фигура, ограниченная
- 45. Формула Ньютона-ЛейбницаТеорема: если функция у = f(x)
- 46. Свойства определенного интеграла
- 47. Свойства определенного интеграла
- 48. Алгоритм вычисления площади криволинейной трапецииСхематично изобразить график
- 49. Вычислить площадь фигуры, ограниченной линиями, используя формулу
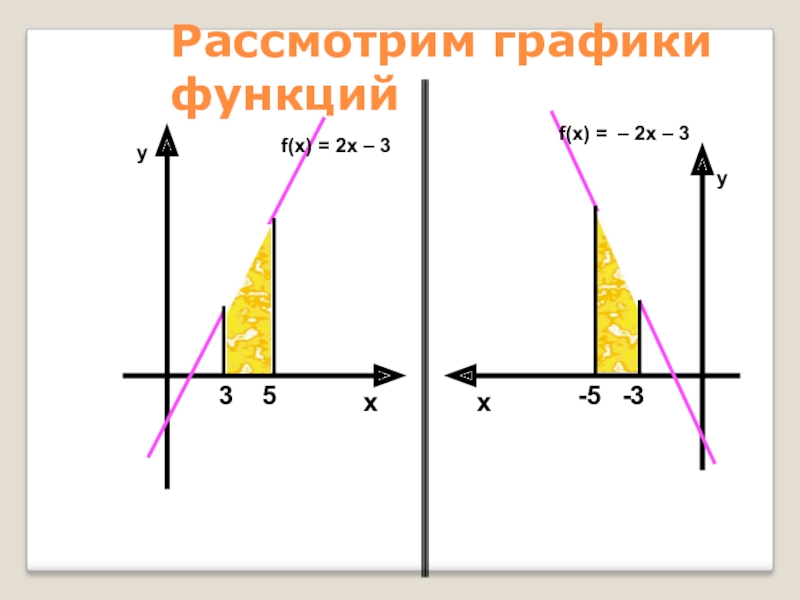
- 50. Рассмотрим графики функцийf(x) = 2x – 3f(x) = – 2x – 3уухх35-5-3
- 51. Проверим решениеЕсли f(x) = 2x – 3Вариант 1.
- 52. Проверим решениеЕсли f(x) = – 2x – 3Вариант 2.
- 53. Вычисление площади плоских фигур с помощью определенного
- 54. Например: Вычислить площадь фигуры, ограниченной графиками функций
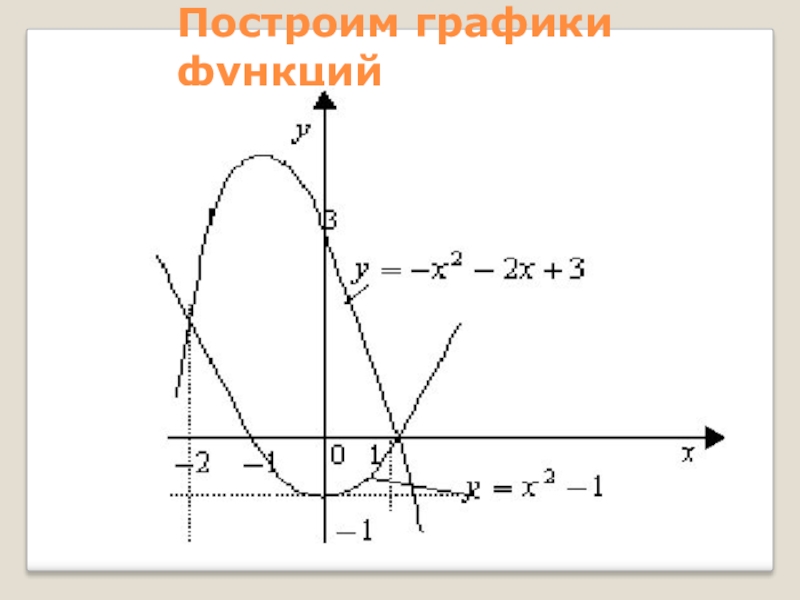
- 55. Построим графики функций
- 56. ЗначитПределы интегрирования: от-2 до1f(x)= - x²-2x+3 g(x)=x² - 1Тогда=
- 57. =
- 58. ЗапомнимГеометрический смысл определенного интеграла – это площадь
- 59. Вычисление объема тела вращенияОбъем тела, образованного вращением
- 60. НапримерНайти объем тела, полученного вращением вокруг оси
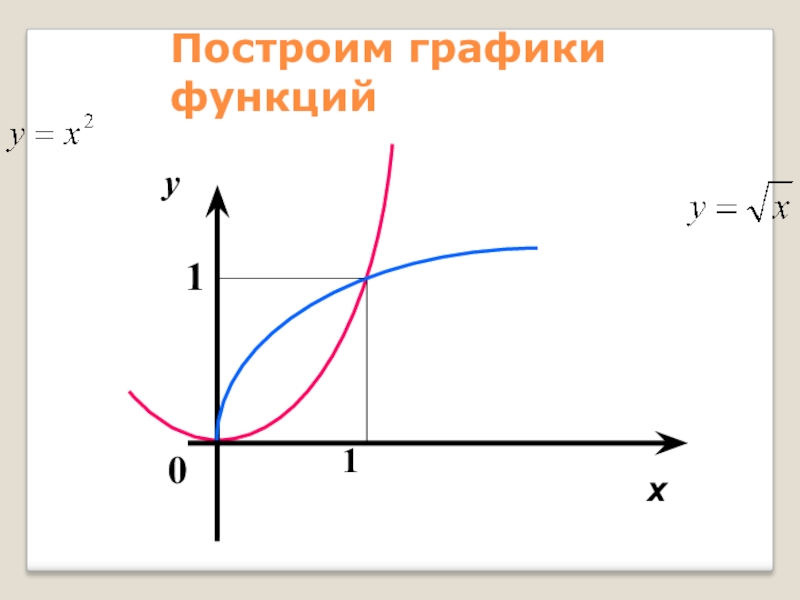
- 61. Построим графики функцийх
- 62. РешениеИскомый объем можно найти какразность объемов, полученныхвращением
- 63. =
- 64. Применение интегралаПлощадь фигурыОбъем тела вращенияРабота электрического зарядаРабота переменной силыМассаПеремещениеДифференциальное уравнениеДавление Количество теплоты
- 65. Найти площадь фигуры, ограниченной линиями 1) y=–3x²–2,
- 66. Работаем по задачникустр. №
- 67. Используемые ресурсыавтор шаблона: Фокина Лидия Петровна, учитель
- 68. Используемые ресурсыhttp://static4.depositphotos.com/1000765/286/i/950/depositphotos_2868805-3d-small---think.jpghttp://awardwinningvideomarketing.com/img/pics/stick_figure_sitting_confused_500_wht.gifhttp://nashashcola.ru/wp-content/uploads/2013/08/Velikie_matematiki-Arhimed_Zakon_Arhimeda-2.jpghttp://cs7010.vk.me/c540102/v540102299/2a4b7/gxoZstcDO4w.jpghttp://cdn2-b.examiner.com/sites/default/files/styles/image_content_width/hash/07/06/07060c3d798d1877de2dffd5882c8dfb.jpg?itok=Bf1WO6a0http://1.bp.blogspot.com/_UAzEooLfuI8/RvU4t7vWjkI/AAAAAAAAA8U/4Yk8JThK_0g/s320/suntzu_portrait-rev.jpg
Слайд 4Определение
Функция F(х) называется первообразной функции f(х) на промежутке Х, если
На
Например: функция у = х² является первообразной для функции у=2х, т.к. для любого х справедливо
(х²)´ = 2х.
Слайд 6Теорема 2
Если F(x) одна из первообразных функции f(x), на промежутке Х,
Слайд 7Таблица первообразных
Зная формулы для нахождения производных, можно составить таблицу
Слайд 8Правила нахождения первообразных
Первообразная суммы равна сумме первообразных
Если F(x) – первообразная для
Если F(x) – первообразная для f(x), то первообразной для функции у= f(кx+m) служит функция у = 1/к· F(кx+ m)
Слайд 9Найдём одну из первообразных
Если f(x) равно:
1) f(x)=2х+х³
2) f(x)=4х-2
3) f(x)=х³-3х²+х-1
4) f(x)=4х⁵+2х+е
5) f(x)=х⁴+3х²+5
6)
Значит F(x) равно:
F(x)= х²+х⁴⁄4
F(x)=2х²-2х
F(x)=х⁴⁄4-2х³+х²⁄2-х
F(x)=2х⁶⁄3+х²+ех
F(x)=х⁵⁄5+х³+5х
F(x)=5sinx+3/2cosx
Слайд 10Ответить на вопрос: какая функция является перообразной для функции
А) cosx - 2sinx
Б) 2cosx - sinx
В) -2cosx - sinx
Г) –cosx + 2sinx
Ответ: в
Слайд 11Выберите ответ, при котором предложение будет верно.
Функция F(x)
если: А) F'(x) = f(x)
Б) F'(x) = - f(x)
В) f'(x) = F(x)
Г) f(x) = F(x)
Ответ: А
Слайд 12Ответить на вопрос: для какой функции первообразной является функция
А) f(x) = 1/4·x⁴+2x³+x²-9x
Б) f(x) = 2x⁴+6x³+x²-9x
В) f(x) = 6x²+12x+1
Г) f(x) = x⁴⁄2+2x³+1/2·x²-9x
Ответ: Г
Слайд 13Ответить на вопрос: производная какой из функций равна у = 4х
А) F(x) = 2x³-2x²+C
Б) F(x) = 2x²-1/3·x+C
В) F(x) = 2x²-x³+C
Г) F(x) = 4x²-x⁴+C
Ответ: В
Слайд 14Задание №1. Найдите первообразную функции f(x), график которой проходит через точку
а) f(x)=5х+х², А(0;3) б) f(x)=3х - 5, А(4;10)
Решение. а) Найдём первообразные
F(x)= 5х²⁄2+х³⁄3+ С, где С – произв.число.
Найдём это С:
т.к. график проходит через точку А(0;3), то
F(0)= 5·0²⁄2+0³⁄3+ С = С и равно 3. С=3
Значит производная, график которой проходит через т. А, имеет вид:
F(x)= 5х²⁄2+х³⁄3+3.
Слайд 15б) f(x)=3х - 5, А(4;10)
Решение. F(x)= 3х²⁄2-5х+С, где С –
F(4)= 3·4²⁄2-5·4+С=24-20+С=4+С и
4+С=10 => С=6, тогда
F(x)= 3х²⁄2-5х+6
Ответ: F(x)= 3х²⁄2-5х+6
Слайд 16Самостоятельно
Найдите первообразную функции f(x), график которой проходит через точку А, если:
2) f(x)=2х²+3, А(-2;-5)
3) f(x)=(х-2)², А(0;2)
4) f(x)=cos3x, А(0;1)
Слайд 17Проверим ответы
1) F(x)= х³⁄3 - 5х + 10
2) F(x)= 2х³⁄3 +
3) F(x)= х³⁄3 - 2х² + 4х + 2
4) F(x)= 1/3·sin3x + 1
Слайд 18Задание №2. Найдите первообразную функции f(x), значение которой при х =
а) f(x)=10х⁴+х; х₀=0; у₀=6
Решение. F(x)= 10х⁵⁄5 + х²⁄2 + С =
= 2х⁵+ х²⁄2 +С, где С – произв. число.
Найдём С. Т.к. по условию F(x₀)=у₀,
то F(0)=2·0⁵+0²⁄2+С=С и равно у₀= 6.
Значит ответ: F(x)=2х⁵+х²⁄2+6
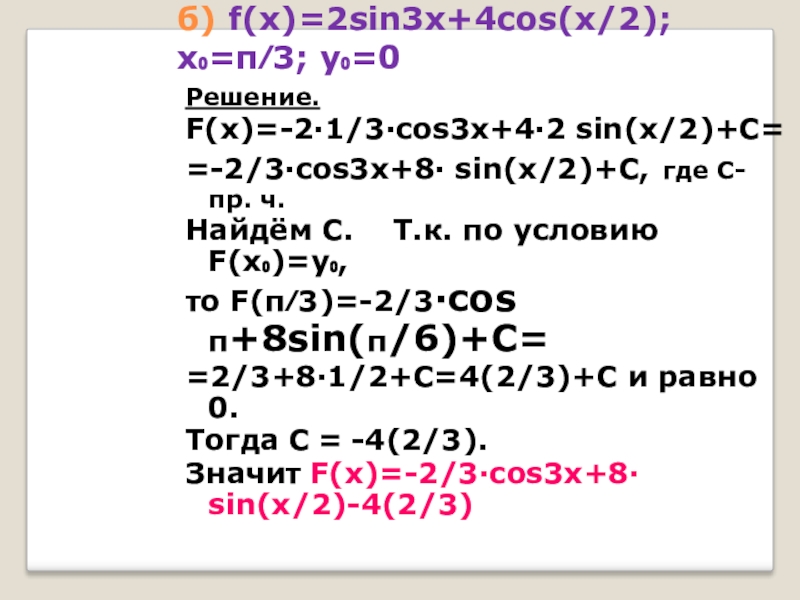
Слайд 19б) f(x)=2sin3x+4cos(x/2); х₀=π⁄3; у₀=0
Решение.
F(x)=-2·1/3·cos3x+4·2 sin(x/2)+С=
=-2/3·cos3x+8· sin(x/2)+С, где С-
Найдём С. Т.к. по условию F(x₀)=у₀,
то F(π⁄3)=-2/3·cos π+8sin(π/6)+С=
=2/3+8·1/2+С=4(2/3)+С и равно 0.
Тогда С = -4(2/3).
Значит F(x)=-2/3·cos3x+8· sin(x/2)-4(2/3)
Слайд 20в) f(x)=4+6х²; х₀=2; у₀
F(2)= 4·2+6·2³⁄3+С= 8+16+С=24+С
и 24+С <0 => С <-24.
Пусть это будет (-25).
Тогда ответ F(x)= 4х+6х³⁄3-25
Слайд 21г) f(x)=2х³+х²+3; х₀=1; у₀>0
Решение. F(x)= 2х⁴⁄4+х³⁄3+3х+С, где С- пр.ч.
Найдём
F(1)= 2·1⁴⁄4+1³⁄3+3·1+С = 3(5/6)+С,
но 3(5/6)+С>0 => С > - 3(5/6)
Пусть С=-1, тогда
F(x)= 2х⁴⁄4+х³⁄3+3х-1
Слайд 22Задание №3. Найдите множество первообразных функции f(x).
а) f(x) =sin²x
Решение.
а) т.к. f(x) =sin²x
= (1 - cos2x)/2 = ½ - 1/2·cos2x,
то одна из первообразных равна:
F(x)=1/2·x - 1/4·sin2x.
Тогда множество всех перообразных равно F(x)=1/2·x-1/4·sin2x + С, где С –пр. число
Слайд 23 б) f(x) = sin5x·cos6x
Решение. т.к. f(x) = sin5x·cos6x =
=1/2·(sin11x-sinx),
то множество всех первообразных данной функции будет равно
F(x) =1/2·(-1/11·cos11x +cosx)+C =
= 1/2· cosx – 1/22 ·cos11x + С
Слайд 28Определение:
Множество всех первообразных функции f(x) на некотором промежутке называется неопределенным
Слайд 29Основные свойства неопределенного интеграла.
т.е. постоянный множитель можно выносить за
Слайд 34Определение
Процесс нахождения интеграла называется интегрированием.
Интегрирование является операцией, обратной
Слайд 35Историческая справка
Интегрирование прослеживается еще в древнем Египте, примерно в 1800 г.
Слайд 36Историческая справка
метод исчерпывания Евдокса (примерно 370 до н.э.), который
Первым известным методом для расчета интегралов является
Слайд 37Историческая справка
Этот метод был подхвачен и развит Архимедом, и
Слайд 38Историческая справка
Аналогичные методы были разработаны не зависимо в Китае в
Слайд 39Историческая справка
Этот метод впоследствии использовали Цзу Чунжи и Цзу Гэн для
Слайд 40Историческая справка
Следующий крупный шаг в исследование интегралов был сделан в Ираке,
( известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени.
Слайд 41Историческая справка
Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла,
Слайд 43Определение
Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и
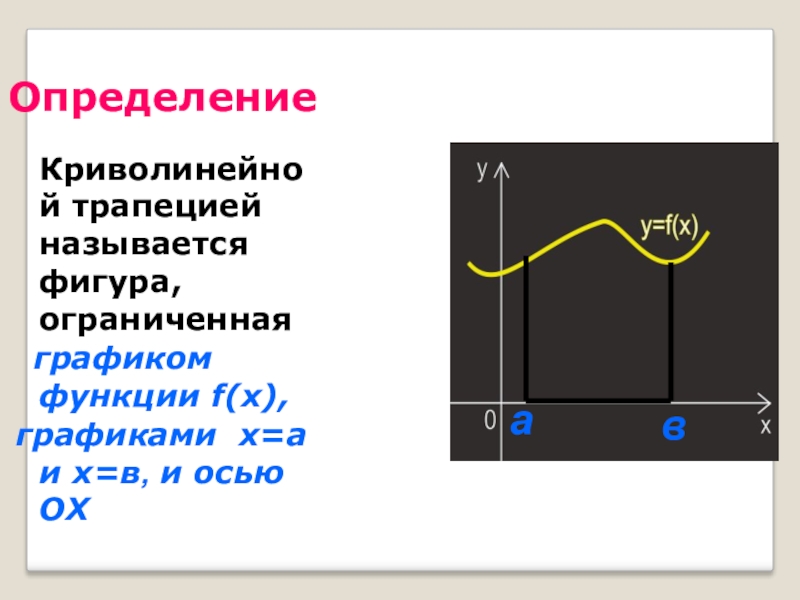
Слайд 44Определение
Криволинейной трапецией называется фигура, ограниченная
графиком функции f(x),
графиками
а
в
Слайд 45Формула Ньютона-Лейбница
Теорема: если функция у = f(x) непрерывна на отрезке [а;в],
Опираясь на эту формулу получаются следующие свойства определенного интеграла
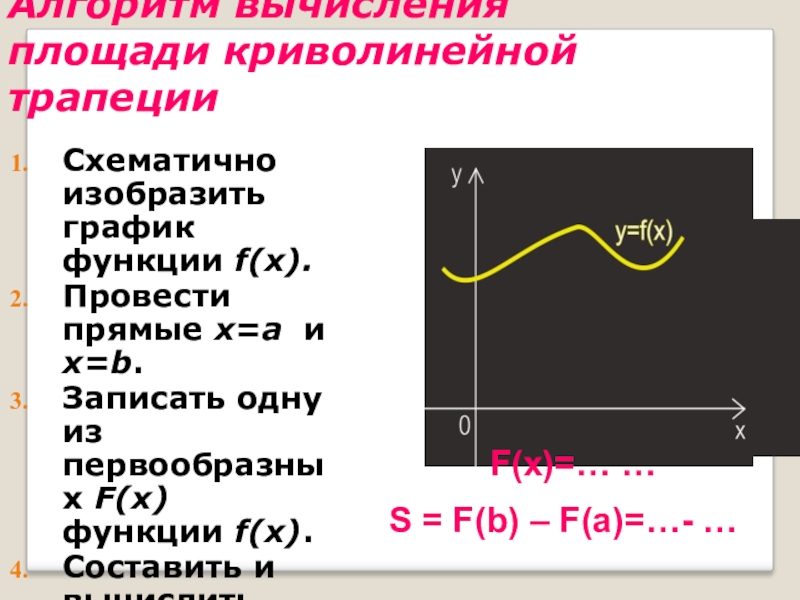
Слайд 48Алгоритм вычисления площади криволинейной трапеции
Схематично изобразить график функции f(x).
Провести прямые x=a
Записать одну из первообразных F(x) функции f(x).
Составить и вычислить разность F(b) – F(a).
F(x)=… …
S = F(b) – F(a)=…- …
Слайд 49Вычислить площадь фигуры,
ограниченной линиями, используя формулу Ньютона-Лейбница
Вариант 1
f(x) = 2x
y = 0,
x = 3,
x = 5
Вариант 2
f(x) = – 2x – 3
y = 0,
x = – 5,
x = – 3
Слайд 53Вычисление площади плоских
фигур с помощью определенного интеграла
Площадь фигуры (S), ограниченной прямыми
непрерывных на отрезке [а;в] и таких, что для любого хє[а;в] выполняется неравенство g(x)≤ f(x), вычисляется по формуле:
Слайд 58Запомним
Геометрический смысл определенного интеграла – это площадь криволинейной трапеции
Физический смысл определенного
(учебник: стр. 291)
Слайд 59Вычисление объема тела вращения
Объем тела, образованного вращением вокруг оси Ox
у =f(x) отрезком оси абсцисс a ≤ x ≤ b и прямыми x=a; x=b, вычисляется по формуле
Слайд 60Например
Найти объем тела, полученного вращением вокруг оси Ox криволинейных трапеций, ограниченных
у= х² и у = √х
Слайд 62Решение
Искомый объем можно найти как
разность объемов, полученных
вращением вокруг оси Ox
криволинейных трапеций,
ограниченных
у = х². Т.е.:
Слайд 64Применение интеграла
Площадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной силы
Масса
Перемещение
Дифференциальное уравнение
Давление
Количество
Слайд 65Найти площадь фигуры, ограниченной линиями
1) y=–3x²–2, x=1, x=2,
2) у= 4x–x², y=0
3) y= x²–2x+3, x+y=5
4) y=x², y=⏐x⏐
Слайд 67Используемые ресурсы
автор шаблона: Фокина Лидия Петровна, учитель начальных классов МКОУ
А.Г. Мордкович. Задачник. Алгебра и начала анализа 10-11 класс, -М., Дрофа,2012
А.Г. Мордкович. Учебник. Алгебра и начала анализа 10-11 класс, -М., Дрофа,2012
Г.В. Дорофеев. Сборник заданий для проведения письменного экзамена по математике за курс средней школы 11 класс. – М., Дрофа, 2008




























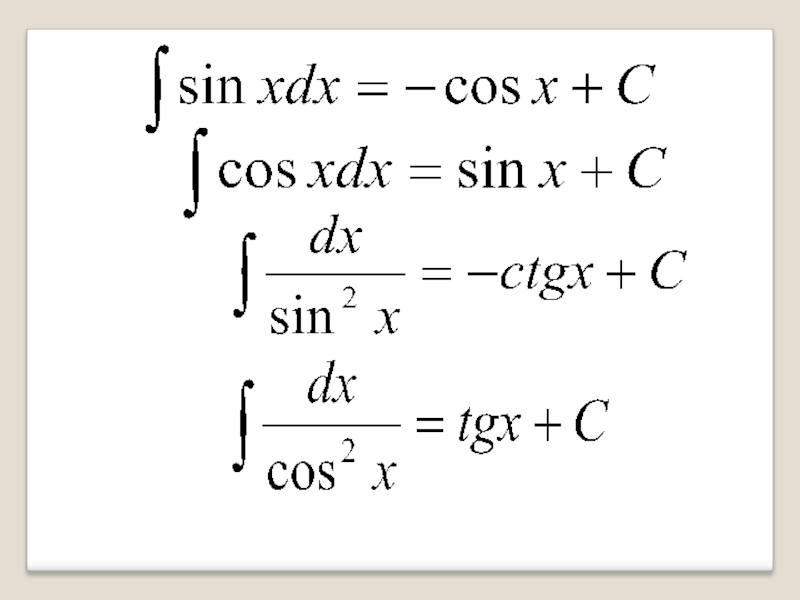










![Презентация по алгебре по теме: Первообразная и интеграл (11 класс) Определение Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и Определение Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и пусть F(x) – некоторая ее первообразная.](/img/thumbs/fc16c9ff29bd1f3dfa9af0162a27b197-800x.jpg)
![Презентация по алгебре по теме: Первообразная и интеграл (11 класс) Формула Ньютона-ЛейбницаТеорема: если функция у = f(x) непрерывна на отрезке [а;в], Формула Ньютона-ЛейбницаТеорема: если функция у = f(x) непрерывна на отрезке [а;в], то справедлива формулаОпираясь на эту формулу](/img/thumbs/f60ee8d052880fe98744355eabbd3841-800x.jpg)