- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре по теме: Графический метод решения квадратных неравенств(8 класс)
Содержание
- 1. Презентация по алгебре по теме: Графический метод решения квадратных неравенств(8 класс)
- 2. Определение Квадратными неравенствами называют неравенства вида ах2+bх+c>0,ах2+bх+c
- 3. По графику функции y= х2 – 6х
- 4. Алгоритм решения квадратного неравенстваНайти корни квадратного трехчлена
- 5. Пример 1Решить неравенство: x2 – 9 ≥
- 6. Пример 2Решить неравенство:− х2 – х +12
- 7. Пример 3Решить неравенство: х2 + 9 >
- 8. Пример 4Решить неравенство: х2 + 9 <
- 9. Пример 5Решить неравенство: - 4х2+12х-9≥0- 4х2+12х-9=0, D
- 10. Пример 6Решить неравенство: - 4х2+12х-9>0- 4х2+12х-9=0, D
- 11. Пример 7Решить неравенство: - 4х2+12х-9≤0- 4х2+12х-9=0, D
- 12. Пример 8Решить неравенство: - 4х2+12х-9
Слайд 2Определение
Квадратными неравенствами называют неравенства вида
ах2+bх+c>0,
ах2+bх+c
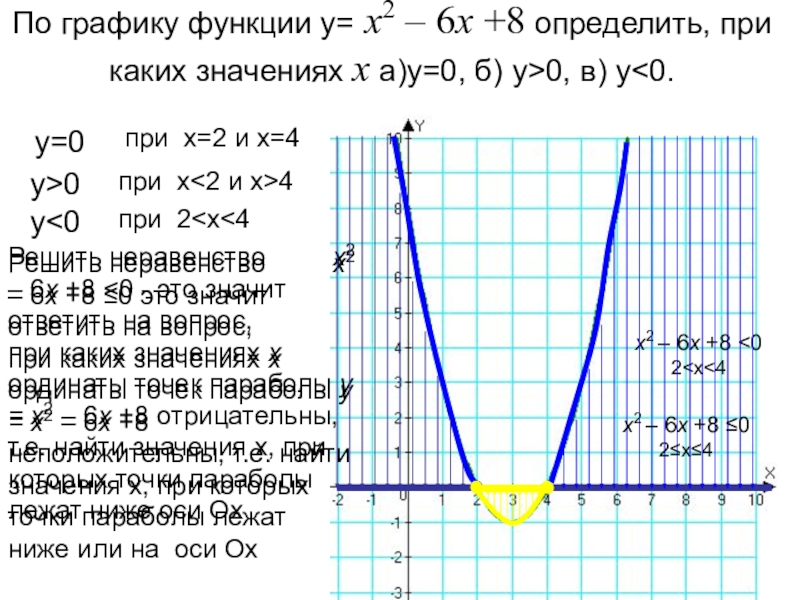
Слайд 3По графику функции y= х2 – 6х +8 определить, при каких
y=0
при х=2 и х=4
y>0
при х<2 и х>4
y<0
при 2<х<4
Решить неравенство х2 – 6х +8 <0 - это значит ответить на вопрос,
при каких значениях х ординаты точек параболы у = х2 – 6х +8 отрицательны, т.е. найти значения х, при которых точки параболы лежат ниже оси Ох
Решить неравенство х2 – 6х +8 ≤0 это значит ответить на вопрос,
при каких значениях х ординаты точек параболы у = х2 – 6х +8 неположительны, т.е. найти значения х, при которых точки параболы лежат ниже или на оси Ох
х2 – 6х +8 <0
2<х<4
х2 – 6х +8 ≤0
2≤х≤4
Слайд 4Алгоритм решения квадратного неравенства
Найти корни квадратного трехчлена ах2+bх+c
Отметить найденные корни на
С помощью полученной геометрической модели определить, на каких промежутках оси х ординаты графика положительны (отрицательны); включить эти промежутки в ответ.
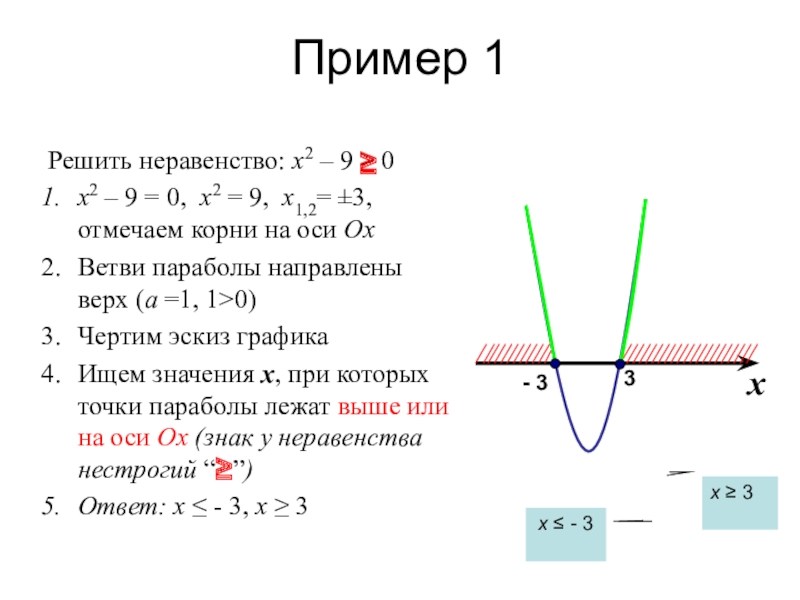
Слайд 5Пример 1
Решить неравенство: x2 – 9 ≥ 0
x2 – 9 =
Ветви параболы направлены верх (а =1, 1>0)
Чертим эскиз графика
Ищем значения х, при которых точки параболы лежат выше или на оси Ох (знак у неравенства нестрогий “≥”)
Ответ: х ≤ - 3, х ≥ 3
- 3
3
х
≥
х ≤ - 3
х ≥ 3
Слайд 6Пример 2
Решить неравенство:
− х2 – х +12 > 0
− х2 –
Ветви параболы направлены вниз (a = - 1, -1< 0)
Чертим эскиз графика
Ищем значения х, при которых точки параболы лежат выше оси Ox (знак у неравенства строгий “>”)
Ответ: - 4 < x < 3
- 4
3
х
>
- 4 < x < 3
Слайд 7Пример 3
Решить неравенство: х2 + 9 > 0
х2 + 9 =
Ветви параболы направлены вверх (а=1,1 > 0 )
Чертим эскиз графика
Ищем значения х при которых график функции расположен выше оси Ох.
Ответ: х – любое число(или (- ∞; + ∞)).
х
Все точки параболы
лежат выше оси Ox.
Неравенство выполняется
при любом значении х
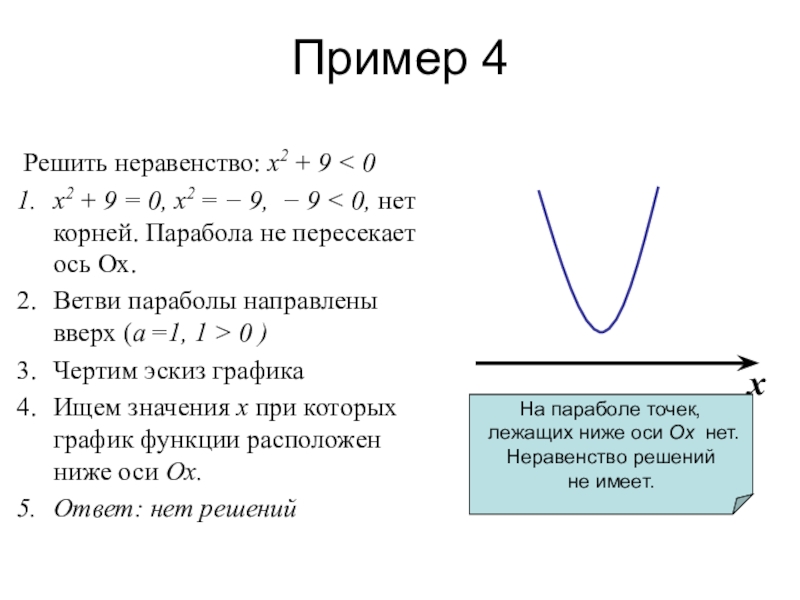
Слайд 8Пример 4
Решить неравенство: х2 + 9 < 0
х2 + 9 =
Ветви параболы направлены вверх (а =1, 1 > 0 )
Чертим эскиз графика
Ищем значения х при которых график функции расположен ниже оси Ох.
Ответ: нет решений
х
На параболе точек,
лежащих ниже оси Ox нет.
Неравенство решений
не имеет.
Слайд 9Пример 5
Решить неравенство:
- 4х2+12х-9≥0
- 4х2+12х-9=0, D = 0, x=1,5
Ветви параболы
Чертим эскиз графика
Ищем значения х, при которых точки параболы расположены выше или на оси Ох
Ответ: х=1,5
х
1,5
Точек, лежащих выше
оси Ох, нет.
На оси Ох только
одна точка.
Ее абсцисса х=1,5 –
решение неравенства
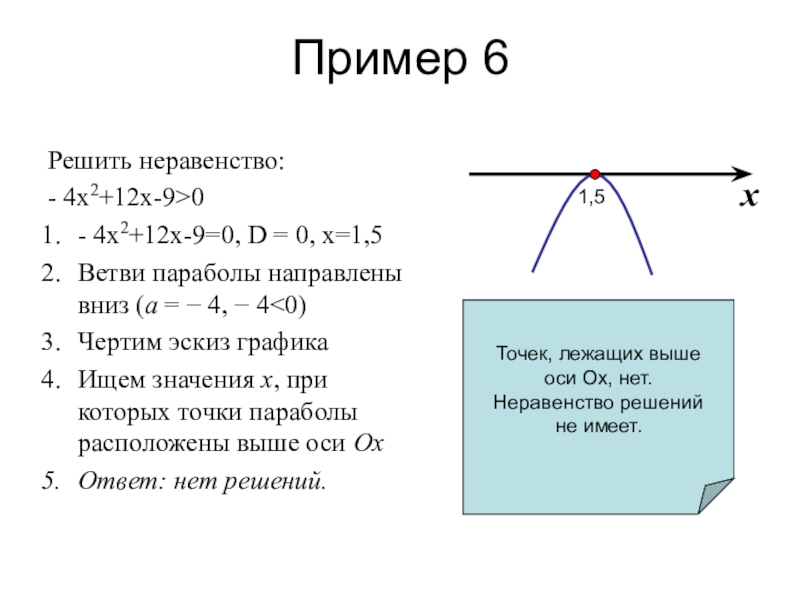
Слайд 10Пример 6
Решить неравенство:
- 4х2+12х-9>0
- 4х2+12х-9=0, D = 0, x=1,5
Ветви параболы
Чертим эскиз графика
Ищем значения х, при которых точки параболы расположены выше оси Ох
Ответ: нет решений.
х
1,5
Точек, лежащих выше
оси Ох, нет.
Неравенство решений
не имеет.
Слайд 11Пример 7
Решить неравенство:
- 4х2+12х-9≤0
- 4х2+12х-9=0, D = 0, x=1,5
Ветви параболы
Чертим эскиз графика
Ищем значения х, при которых точки параболы расположены ниже или на оси Ох
Ответ: х – любое число.
х
1,5
Каждая из точек параболы
лежит либо ниже либо на
оси Ох.
Неравенство выполняется
при любых значениях х
Слайд 12Пример 8
Решить неравенство:
- 4х2+12х-9
Чертим эскиз графика
Ищем значения х, при которых точки параболы расположены ниже оси Ох
Ответ: х ≠1,5 (или (− ∞; 1,5)∪(1,5; +∞)).
х
1,5
При всех значениях х ,
кроме х = 1,5
точки параболы
расположены
ниже оси Ох