- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Наименьшее и наибольшее значения функции (10 класс)
Содержание
- 1. Презентация по алгебре Наименьшее и наибольшее значения функции (10 класс)
- 2. Пусть у нас есть график некоторой функции
- 3. А как же быть в других случаях,
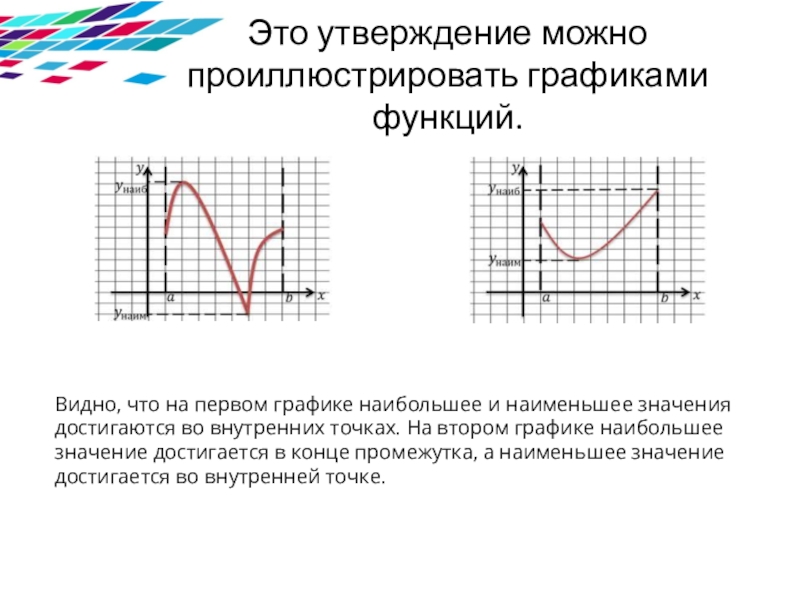
- 4. Это утверждение можно проиллюстрировать графиками функций.Видно, что
- 5. Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [a; b].
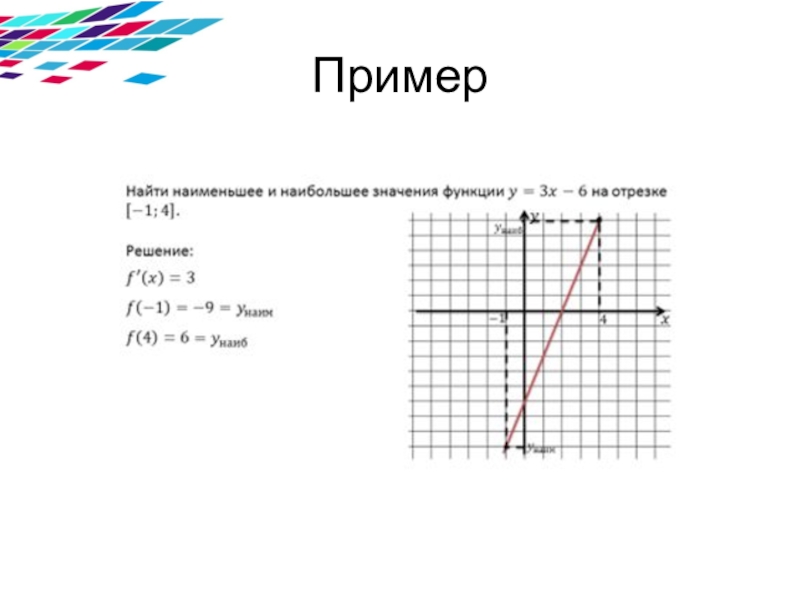
- 6. Пример
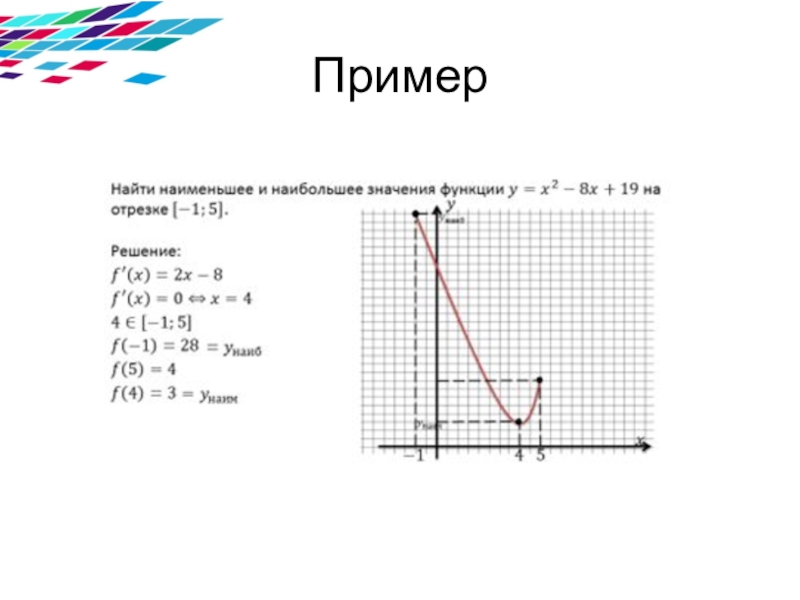
- 7. Пример
- 8. Надо найти наибольшее и наименьшее значения на
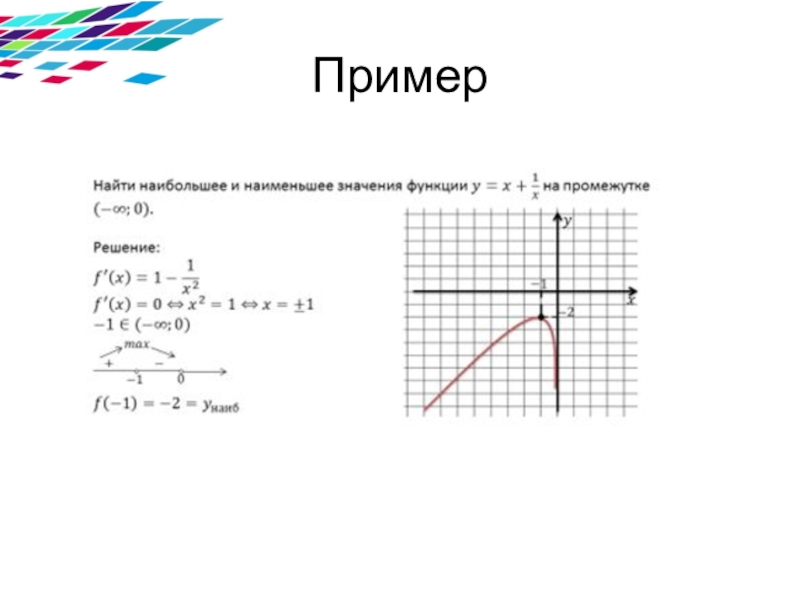
- 9. Пример
- 10. Пример
Слайд 1Наибольшее и наименьшее значения непрерывной
функции на промежутке
10 класс
МАОУ СОШ №
Слайд 2Пусть у нас есть график некоторой функции f(x) на промежутке [a;
Слайд 3А как же быть в других случаях, когда наличие наибольшего и
Для того, чтобы избежать построения графика функции воспользуемся следующими утверждениями.
Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего, и своего наименьшего значений.
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3. Если наибольшее или наименьшее значение достигается внутри отрезка, то только в стационарной или критической точке.
Слайд 4Это утверждение можно проиллюстрировать графиками функций.
Видно, что на первом графике наибольшее
Слайд 5Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x)
Слайд 8Надо найти наибольшее и наименьшее значения на незамкнутом интервале
Теорема.
Пусть функция y
а) если x = x0 − точка максимума, то yнаиб = f(x0);
б) если x = x0 − точка минимума, то yнаим = f(x0).

![Презентация по алгебре Наименьшее и наибольшее значения функции (10 класс) Пусть у нас есть график некоторой функции f(x) на промежутке [a; Пусть у нас есть график некоторой функции f(x) на промежутке [a; b]. По графику легко найти наибольшее](/img/thumbs/e263edd367d9c1dc8155d91ed4207af3-800x.jpg)

![Презентация по алгебре Наименьшее и наибольшее значения функции (10 класс) Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [a; b]. Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [a; b].](/img/thumbs/a027e21178fb4632892bdd31d4acc330-800x.jpg)