Автор работы: Несивкина Галина Анатольевна ,учтель математики первой квалификационной категории
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на темуГрафический способ решения систем алгебраических уравнений с использованием программного пакета MathCAD (7 класс)
Содержание
- 1. Презентация по алгебре на темуГрафический способ решения систем алгебраических уравнений с использованием программного пакета MathCAD (7 класс)
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. ПроблемаНеобходимо найтиудобный, наглядный,
- 6. Слайд 6
- 7. Слайд 7
- 8. Алгоритм построения графика линейного
- 9. Алгоритм построения графика линейного уравнения с помощью
- 10. 1.1Алгоритм построения графика линейного уравнения с помощью
- 11. 1.1 Алгоритм построения графика линейного
- 12. Установить курсор справа от
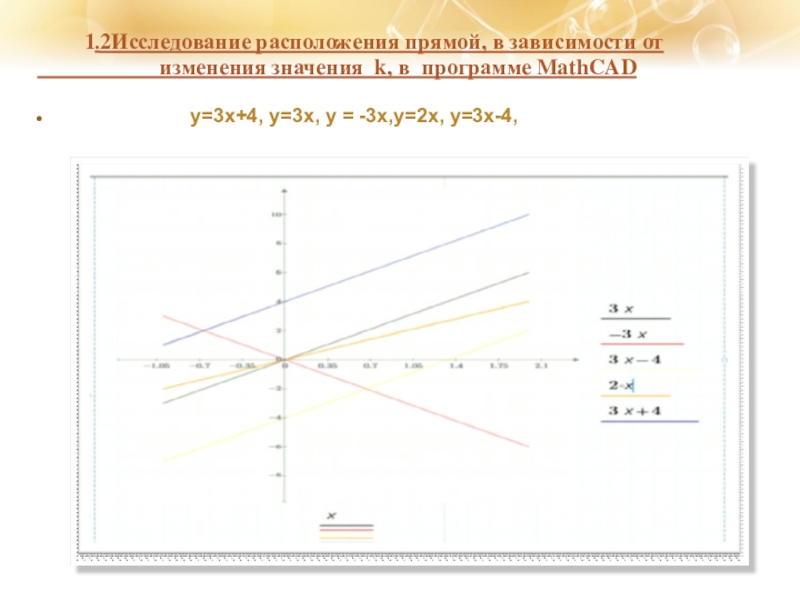
- 13. 1.2Исследование расположения прямой,
- 14. Слайд 14
- 15. Слайд 15
- 16. 1.3.Алгоритм графического метода решения систем
- 17. Слайд 17
- 18. Литератураhttps://www.ptcusercommunity.com/community/mathcadhttps://www.ptcusercommunity.com/docs/DOC-3621http://127.0.0.1:62221/hcHelpru/hcHelp/HCHLearningConnector.html#HCHLearningConnector_MathcadLearningConnector-A80901381_12
Слайд 1Графический способ решения систем
алгебраических уравнений с использованием
программного пакетаMathCAD
МБОУ «Ширинская»
Слайд 2
Алгоритм построения графика линейного уравнения с помощьюMathCAD
Исследование расположения прямой, в зависимости от изменения значения в программе MathCAD
Алгоритм графического метода решения систем
линейных уравнений с помощью программыMathCAD
Слайд 3 Введение
Актуальность
Для изучения и глубокого исследования следующих разделов
математики:взаимное расположение графиков линейных
функций , графический способ решения системы линейных
уравнений , отводиться мало времени.
Так,как этот материал прослеживается в различных заданиях
повышенной сложности, в задачах математических олимпиад, в заданиях на ОГЭ, на ЕГЭ, то он требует детального рассмотрения и изучения.
Слайд 4
Как увеличить время на изучение тем:
взаимное расположение графиков линейных функций
графический способ решения системы уравнений
Слайд 5 Проблема
Необходимо найти
удобный, наглядный, а самое главное быстрый
построения графиков
уравнений
Гипотеза
Объект исследования
«Линейная функция»
(А.Г.Мордкович, Алгебра 7 класс.глава2)
«Системы двух линейных уравнений с двумя
переменными»(глава3)
Слайд 6 Цель работы
Показать графический
алгебраических уравнений с применением инженерного
программного пакета MathCAD.
Исследование предоставляет базовые знания работы с
программой, как они могут быть применены для решения
системы двух линейных уравнений с двумя переменными
графическим методом.
Слайд 7 Перспективы
Использовать программный продукт,
изучения программного материала, решения задач повышенной
сложности ,решения заданий из ОГЭ.
В данной работе были рассмотрены примеры, каким образом
решаются на базе этой программы разнообразные математические
задачи.
Данная работа поможет ученикам быстро освоить основные навыки
работы с этой программой, а примеры и способы решения помогут их
закрепить для решения новых задач.
Слайд 8 Алгоритм построения графика линейного уравнения с помощью
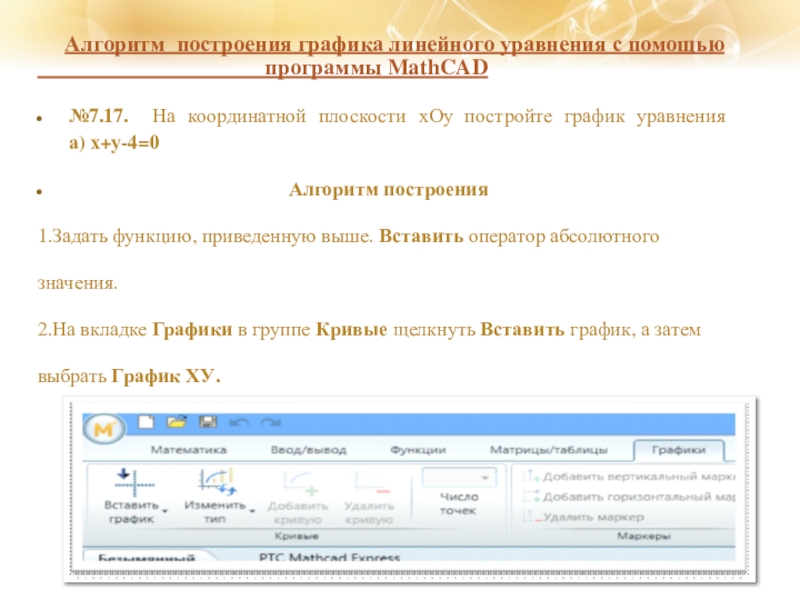
№7.17. На координатной плоскости хОу постройте график уравнения а) х+у-4=0
Алгоритм построения
1.Задать функцию, приведенную выше. Вставить оператор абсолютного
значения.
2.На вкладке Графики в группе Кривые щелкнуть Вставить график, а затем
выбрать График ХУ.
Слайд 9Алгоритм построения графика линейного уравнения с помощью
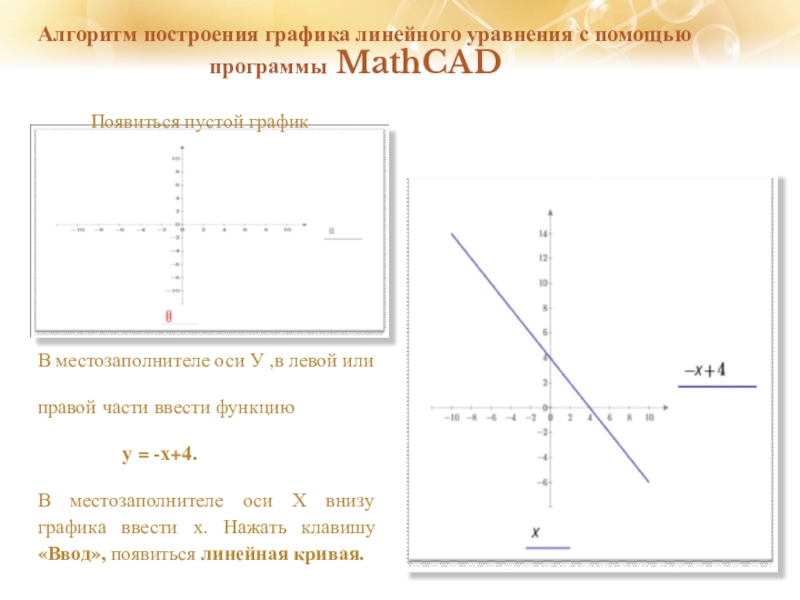
В местозаполнителе оси У ,в левой или
правой части ввести функцию
у = -х+4.
В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная кривая.
Появиться пустой график
Слайд 101.1Алгоритм построения графика линейного уравнения с помощью
№8.28. Постройте график линейной функции у = х+4 и у=2х
Найдите:
а) координаты точек пресечения графика с осями координат;
б) значение у, соответствующее значению х=--2;-1;1.
в ) значение х ,которому соответствует значение у, равное-2;2;4.
Слайд 11 1.1 Алгоритм построения графика линейного уравнения с помощью
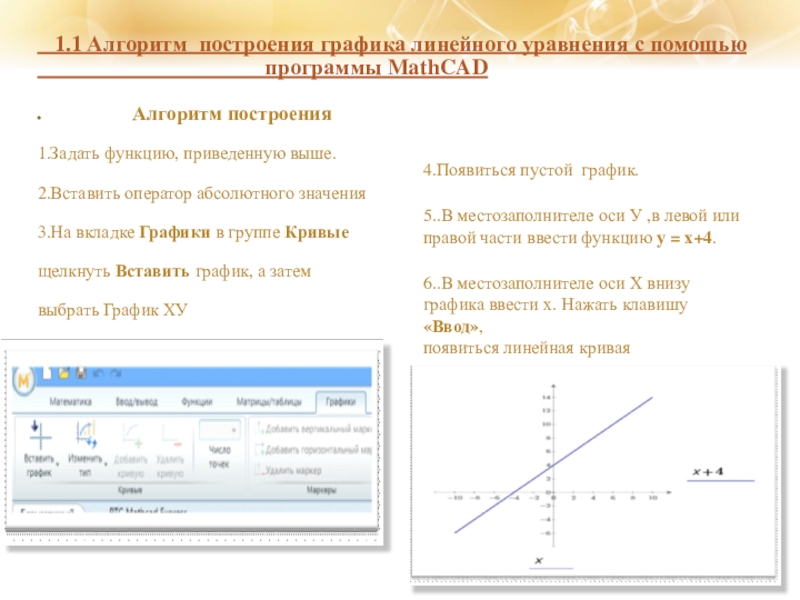
Алгоритм построения
1.Задать функцию, приведенную выше.
2.Вставить оператор абсолютного значения
3.На вкладке Графики в группе Кривые
щелкнуть Вставить график, а затем
выбрать График ХУ
4.Появиться пустой график.
5..В местозаполнителе оси У ,в левой или правой части ввести функцию у = х+4.
6..В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод»,
появиться линейная кривая
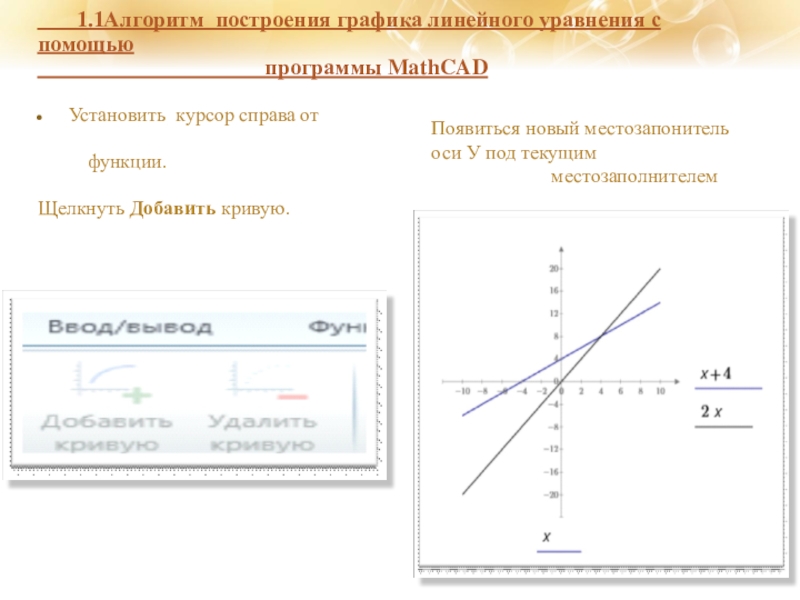
Слайд 12Установить курсор справа от
функции.
Щелкнуть
1.1Алгоритм построения графика линейного уравнения с помощью
программы MathCAD
Появиться новый местозапонитель
оси У под текущим
местозаполнителем
Слайд 13 1.2Исследование расположения прямой, в зависимости от
у=3х+4, у=3х, у = -3х,у=2х, у=3х-4,
Слайд 14
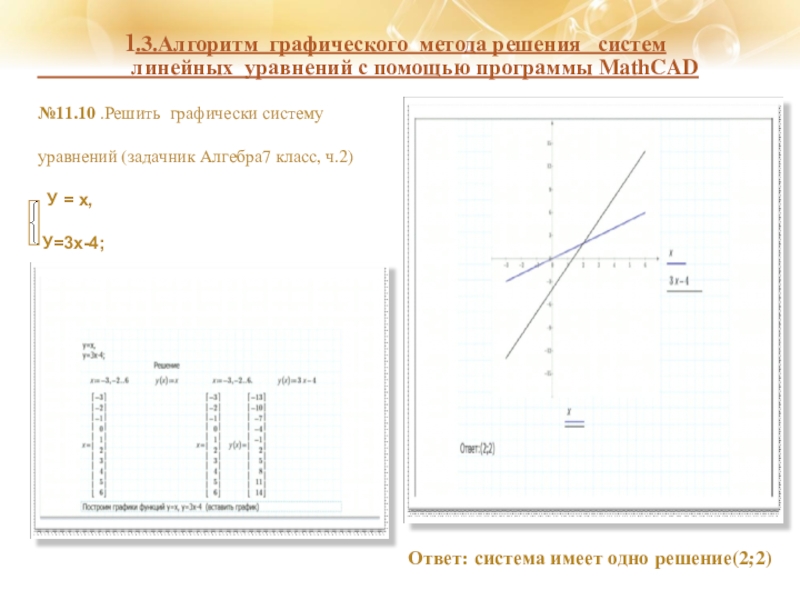
№11.10 .Решить графически систему
уравнений (задачник Алгебра7 класс, ч.2)
У = х,
У=3х-4;
Ответ: система имеет одно решение(2;2)
Слайд 15 1.3.Алгоритм графического метода
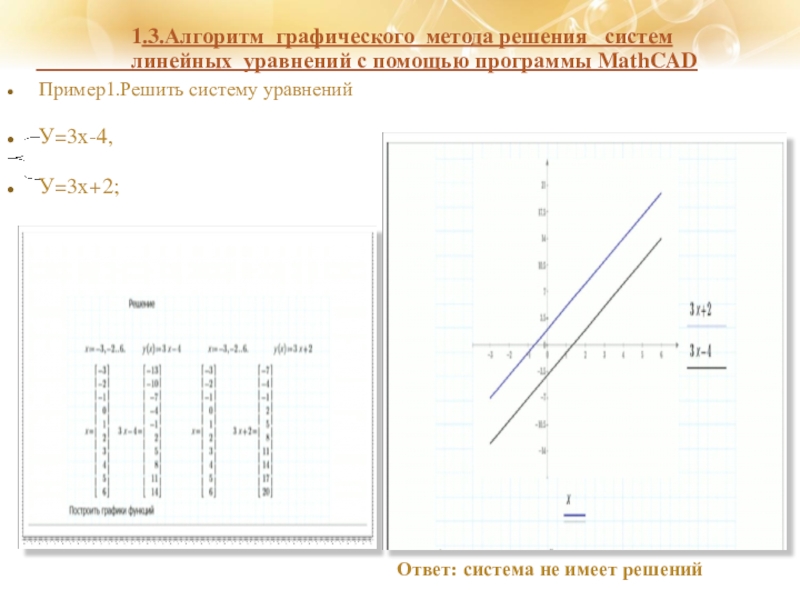
Пример1.Решить систему уравнений
У=3х-4,
У=3х+2;
Ответ: система не имеет решений
Слайд 161.3.Алгоритм графического метода решения систем
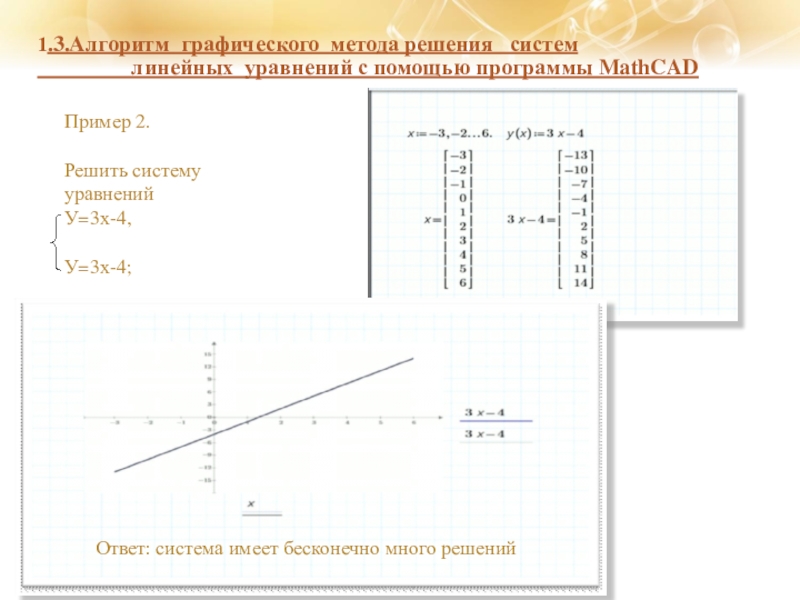
Пример 2.
Решить систему уравнений
У=3х-4,
У=3х-4;
Ответ: система имеет бесконечно много решений
Слайд 17
Графический метод решения системы линейных уравнений имеет
большое значение. С его помощью можно сделать следующие важные
выводы:
- графиком обоих уравнений системы линейных уравнений являются
прямые;
-эти прямые могут пересекаться, причем только в одной точке,- это
значит, что система имеет единственное решение;
-эти прямые могут быть параллельны - это значит, что система
не имеет решений( система несовместна);
-эти прямые могут совпасть - это значит, что система имеет
бесконечно много решений (система не определена).