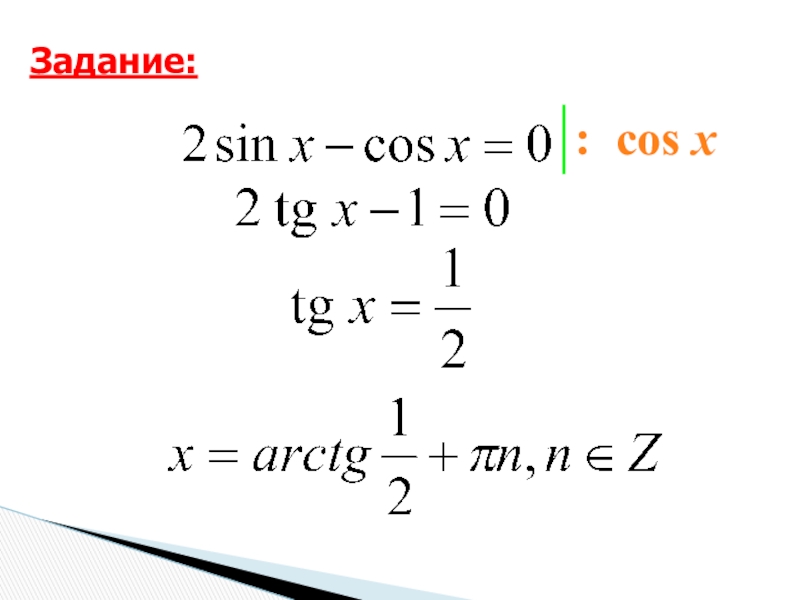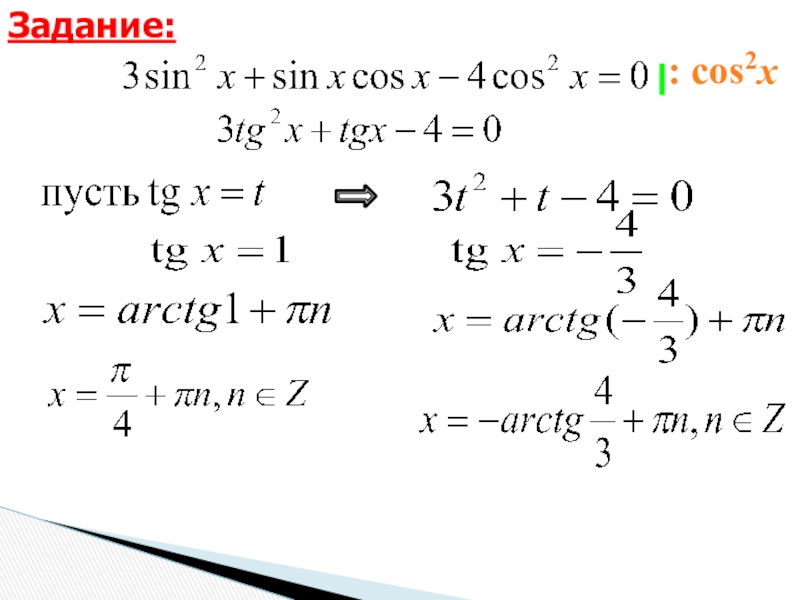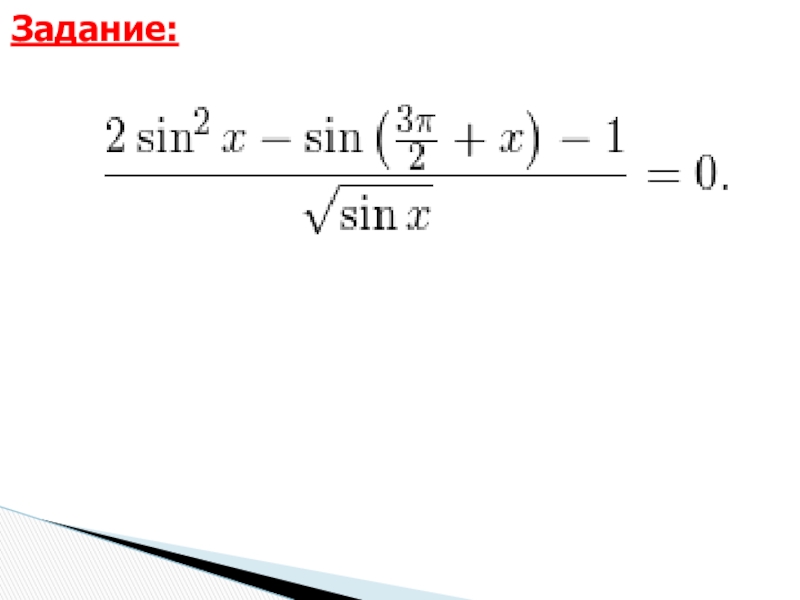- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Тригонометрические уравнения
Содержание
- 1. Презентация по алгебре на тему Тригонометрические уравнения
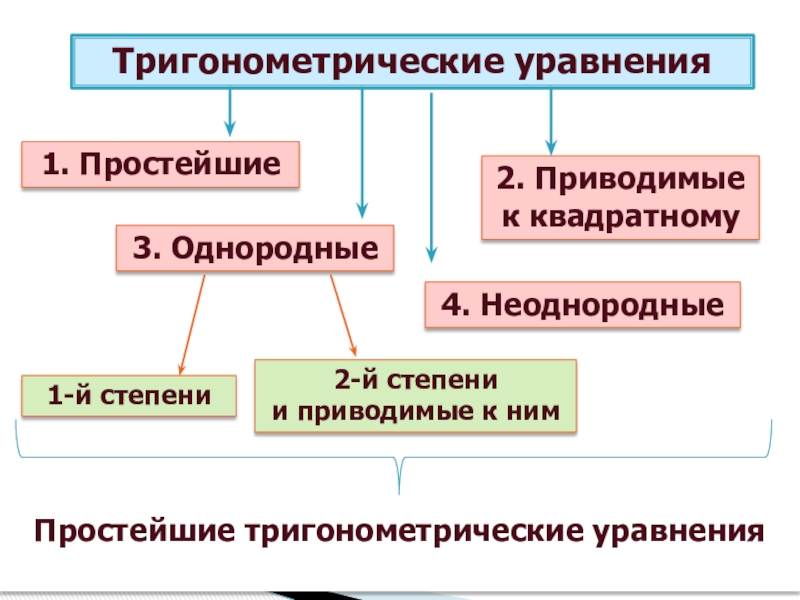
- 2. Простейшие тригонометрические уравненияТригонометрические уравнения1. Простейшие2. Приводимые к квадратному3. Однородные4. Неоднородные1-й степени2-й степени и приводимые к ним
- 3. Формулы решения уравнений arctg(-a) = - arctg a
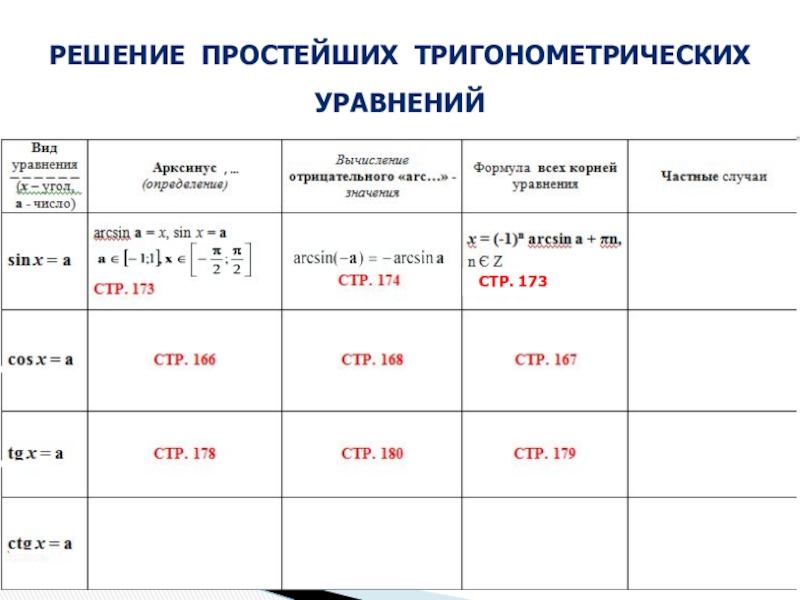
- 4. Решение простейших тригонометрических уравнений
- 5. Слайд 5
- 6. Слайд 6
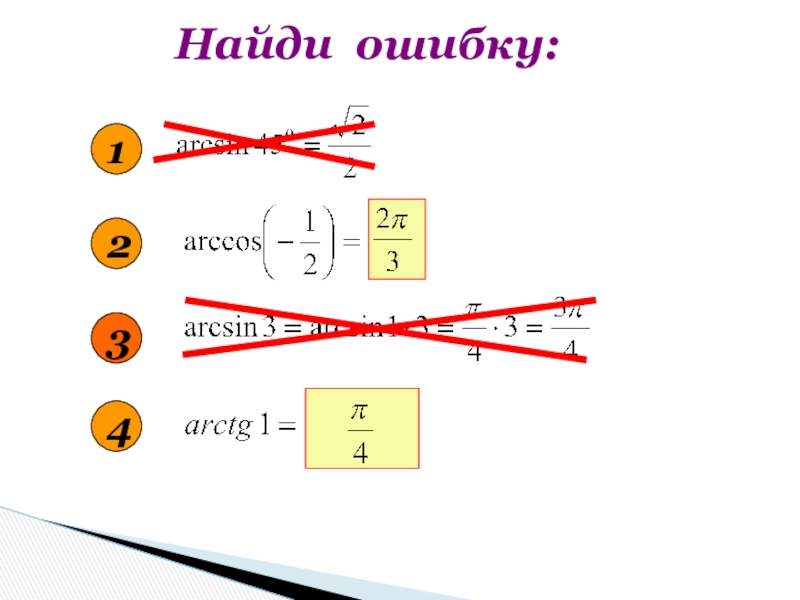
- 7. Найди ошибку:1234
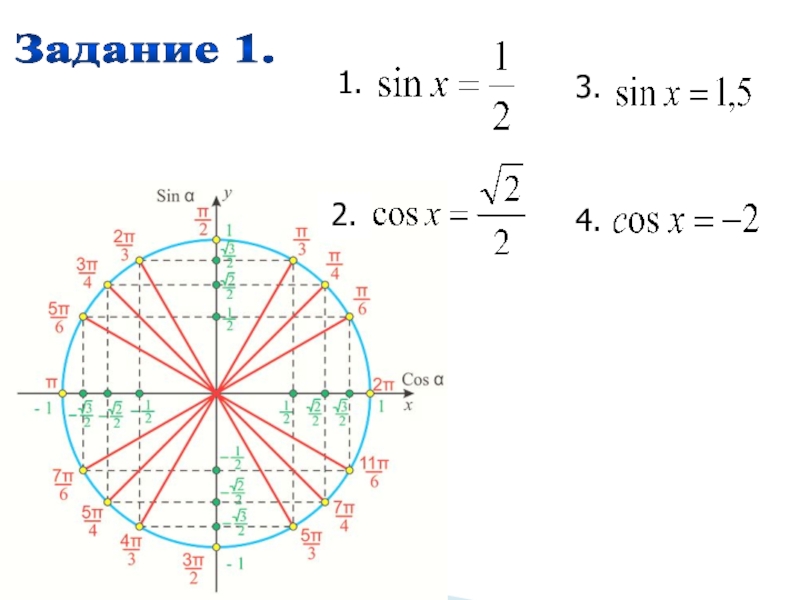
- 8. Задание 1.
- 9. Установите соответствие:sin x = 0 sin x
- 10. Тренажер:
- 11. Проверь себя:
- 12. 1. Алгебраический метод (метод замены переменной и
- 13. Задание: (Переход к половинному углу.)4
- 14. Задание:
- 15. Задание: Дано уравнение а) Решите уравнение.б) Укажите корни, принадлежащие отрезку
- 16. Однородные тригонометрические уравнения
- 17. : cos xЗадание:
- 18. : cos2xЗадание:
- 19. Задание:
- 20. Задание:
- 21. Слайд 21
- 22. 1) Решить уравнение:
- 23. Определите вид уравнения и укажите способ его
- 24. Введение вспомогательного угла. Рассмотрим уравнение вида:
- 25. Универсальная подстановка. Решить уравнение: 3 sin
Простейшие тригонометрические уравненияТригонометрические уравнения1. Простейшие2. Приводимые к квадратному3. Однородные4. Неоднородные1-й степени2-й степени и приводимые к ним
Слайд 2
Простейшие тригонометрические уравнения
Тригонометрические уравнения
1. Простейшие
2. Приводимые к квадратному
3. Однородные
4. Неоднородные
1-й степени
2-й
степени
и приводимые к ним
и приводимые к ним
Слайд 9Установите соответствие:
sin x = 0
sin x = - 1
sin
x = 1
cos x = 0
cos x = 1
tg x = 1
cos x = -1
1
2
3
4
5
6
7
Слайд 121. Алгебраический метод (метод замены переменной и подстановки , преобразование произведения
в сумму, переход к половинному углу. ..)
Методы решения тригонометрических уравнений
2. Разложение на множители.
4. Приведение к однородному уравнению.
Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла.
3. Введение вспомогательного угла.
Слайд 16Однородные тригонометрические уравнения – уравнения относительно синуса и
косинуса, все члены которого имеют одинаковую степень и одинаковые углы
Слайд 221) Решить уравнение:
cos 2 x + sin x · cos x = 1.
2) Решить уравнение:
cos 2x – cos 8x + cos 6x = 1.
3) Решить уравнение:
cos 2x – cos 8x + cos 6x = 1.
Слайд 23Определите вид уравнения и укажите
способ его решения:
а) sin x = 2 cos x;
б) sin x + cos x = 0;
в) 4 cos 3x + 5 sin 3x = 0;
г) 1 +7 cos²x + 3 sin²x = 0;
д) sin 3x – cos 3x = 0;
е) sin x cos x + cos²x = 0
б) sin x + cos x = 0;
в) 4 cos 3x + 5 sin 3x = 0;
г) 1 +7 cos²x + 3 sin²x = 0;
д) sin 3x – cos 3x = 0;
е) sin x cos x + cos²x = 0
Слайд 24Введение вспомогательного угла.
Рассмотрим уравнение вида: a sin x +
b cos x = c ,
где a, b, c – коэффициенты; x – неизвестное.
где a, b, c – коэффициенты; x – неизвестное.
Тогда можно обозначить их соответственно как cos и sin ( здесь - так называемый вспомогательный угол ), и наше уравнение принимает вид:
Слайд 25Универсальная подстановка.
Решить уравнение: 3 sin x – 4 cos
x = 3. Таким образом, решение даёт только первый случай.
