- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Теорема Виета
Содержание
- 1. Презентация по алгебре на тему Теорема Виета
- 2. Цели урока: доказать теорему Виета; показать
- 3. 1. Назвать корни уравнений:x2 = 64x2+3x =
- 4. 2. Указать коэффициенты квадратных уравнений:2x2-5x+10=02+x+x2=05x2-4x=36x- x2=011-2x2=4x
- 5. 3. Решить уравнение:х2-6x+8=0
- 6. Установим связь между корнями приведенного квадратного уравнения
- 7. Теорема Виета Сумма корней приведенного квадратного
- 8. Историческая справка Впервые эти выводы
- 9. Доказательство теоремы:
- 10. Тренировочные задания
- 11. Проанализируйте данные и узнайте числа m
- 12. Следствие 1Не решая уравнения, можно
- 13. 1. Не решая уравнение, определите знаки его
- 14. х2 + bx + c = 0x1
- 15. х2 + bx + c = 0x1
- 16. х2 + bx + c = 0x1
- 17. Примеры x2 +
- 18. 1) х² - 2х - 8
- 19. Если квадратное уравнение не является приведенным, то как будет выглядеть теорема Виета?
- 20. ax² + bх
- 21. Слайд 21
- 22. Теорема ВиетаПо праву достойна в
- 23. Следствие 2 Если
- 24. Обратная теорема
- 25. Тренировочные задания
- 26. Составьте квадратное уравнение, имеющее заданные корни х1
- 27. ПРИМЕНЕНИЕ ТЕОРЕМЫПроверяем, правильно ли найдены корни уравнения.Определяем
Слайд 2 Цели урока:
доказать теорему Виета;
показать ее применение;
рассмотреть различные
на применение теоремы Виета.
Слайд 6Установим связь между корнями приведенного квадратного уравнения и его коэффициентами.
х1 =
2
- 3
х1 = 1, х2 = - 6
- 5
- 6
х1 = 4, х2 = - 3
1
- 12
х1 = - 4, х2 = - 3
- 7
12
х1 = 5, х2 = 3
8
15
Какие выводы мы можем сделать?
Слайд 7Теорема Виета
Сумма корней приведенного квадратного уравнения равна второму
х2+bх+c=0
х1 и х2- корни
х1+х2=-b, х1·х2=c
Эта зависимость называется «теоремой Виета»,
доказана в 1591 году
Слайд 8Историческая справка
Впервые эти выводы сделал Франсуа Виет (1540
Он стал одним из первых, кто стал обозначать числа буквами, что существенно развило теорию уравнений. Свои выводы Франсуа Виет сформулировал в виде теоремы и доказал ее. Использование этой теоремы позволяет экономить время при решении уравнений.
Слайд 9 Доказательство теоремы:
Дано:
Доказать: x1 + x2 = - b, х1 ·х2 = c.
Доказательство:
Слайд 10Тренировочные задания
Если данное уравнение имеет корни
(D=100-84>0),то их можно подобрать по формулам Виета.
Выпишем пары чисел, произведение которых равно 21: 1 и 21; 3 и 7; -1 и -21; -3 и -7.
Выберем ту, сумма которой равна – 10.
Тогда: x= -3; x= -7.
Слайд 11Проанализируйте данные
и узнайте числа m и n
а)
m = ______ n = _______
б) m · n = 15 ; m + n = - 8
m = ______ n = _______
в) m + n = - 2 ; m · n = - 35
m = ______ n = _______
г) m + n = 1 ; m · n = - 12
m = ______ n = _______
7
2
- 3
- 5
- 7
5
4
- 3
Слайд 12 Следствие 1
Не решая уравнения, можно определить знаки
и относительные
c>0, b>0, оба отрицательные;
c>0, b<0, оба положительные;
c<0, b>0, разных знаков, но отрицательный
по модулю больше;
c<0, b<0, разных знаков, но положительный
по модулю меньше.
Слайд 131. Не решая уравнение, определите знаки его корней:
1)
2) х2 + 36х + 315 = 0;
3) х2 – 40х + 364 = 0;
4) х2 – 30х + 250 = 0.
2. Не применяя формулу корней, найдите второй корень уравнения, если известен первый:
1) х2 + 45х – 364 = 0, х1 = 7;
2) х2 – 40х + 364 = 0, х1 =14.
Тренировочные задания
Слайд 14
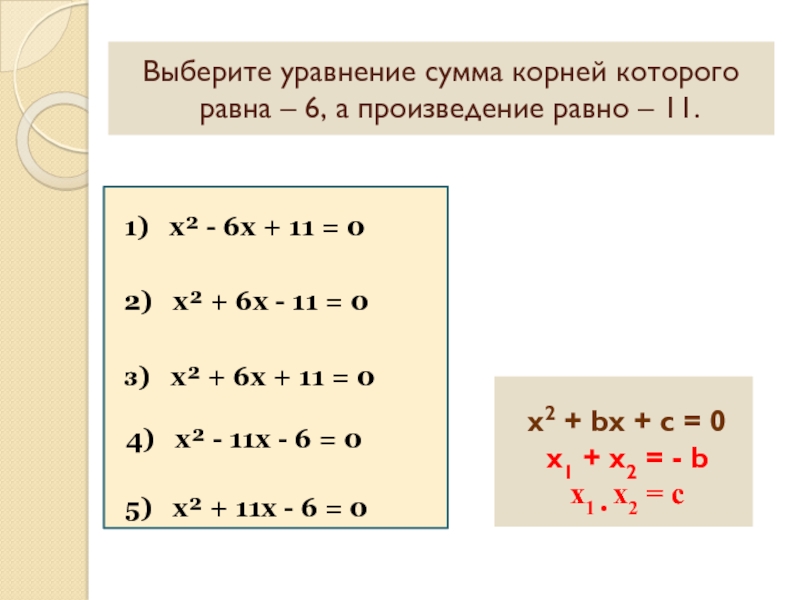
х2 + bx + c = 0
x1 + x2 = -
x1 • x2 = c
Выберите уравнение сумма корней которого
равна – 6, а произведение равно – 11.
1) х² - 6х + 11 = 0
2) х² + 6х - 11 = 0
з) х² + 6х + 11 = 0
4) х² - 11х - 6 = 0
5) х² + 11х - 6 = 0
Слайд 15
х2 + bx + c = 0
x1 + x2 = -
x1 • x2 = c
Если х1 = - 5 и х2 = - 1 корни уравнения
х² + px + q = 0, то
1) p = - 6 , q = - 5
2) p = 5 , q = 6
з) p = 6 , q = 5
4) p = - 5 , q = - 6
5) p = 5 , q = - 6
Слайд 16
х2 + bx + c = 0
x1 + x2 = -
x1 • x2 = c
Найдите сумму и произведение корней уравнения х² - 3х – 5 = 0
(выберите правильный ответ ).
1) х1 + х2= - 3, х1 • х2 = - 5
2) х1 + х2= - 5, х1 • х2 = - 3
З) х1 + х2= 3, х1 • х2 = - 5
4) х1 + х2= 5, х1 • х2 = - 3
Слайд 17 Примеры
x2 + 10x – 24 =
x2 – 7x + 12 = 0
x1 +x2 = -10
x1 x2 = -24
x1 + x2 = 7
x1 x2 = 12
-6 4
-4 6
-8 3
-3 8
-12 2
-2 12
-1 24
1 -24
1 12
6
4
Слайд 181) х² - 2х - 8 = 0
2) х²
з) х² - 8х - 9 = 0
Д > 0, х1 + х2 = 2, х1 ∙ х2 = - 8
Д > 0, х1 + х2 = - 7, х1 ∙ х2 = 12
Д > 0, х1 + х2 = 8, х1 ∙ х2 = - 9
х1 = - 2 , х2 = 4
х1 = - 3 , х2 = - 4
х1 = - 1 , х2 = 9
Тренировочные задания
Для каждого уравнения попытайтесь подобрать два числа х1 и х2 так, чтобы выполнялись получившиеся равенства.
Слайд 20 ax² + bх + с = 0
По теореме Виета
x1 + x2 = - b/a
x1 ∙ x2 = c/a
Используя теорему Виета, можно выразить сумму и произведение корней произвольного квадратного уравнения через его коэффициенты.
Слайд 22 Теорема Виета
По праву достойна в стихах быть воспета
О свойствах
Что лучше, скажи, постоянства такого?
Умножишь ты корни – и дробь уж готова.
В числителе c, в знаменателе a
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда
В числителе b, в знаменателе a ?!
Слайд 23 Следствие 2
Если сумма коэффициентов квадратного уравнения
а) а+b+с=0, x1= 1, x2= c/a.
б) а-b+c=0, x1= - 1, x2 = - c/a.
Например: x²+17x-18=0, (1;-18)
x²-39x-40=0, (-1;40)
2x²-x-3=0, (-1;1,5)
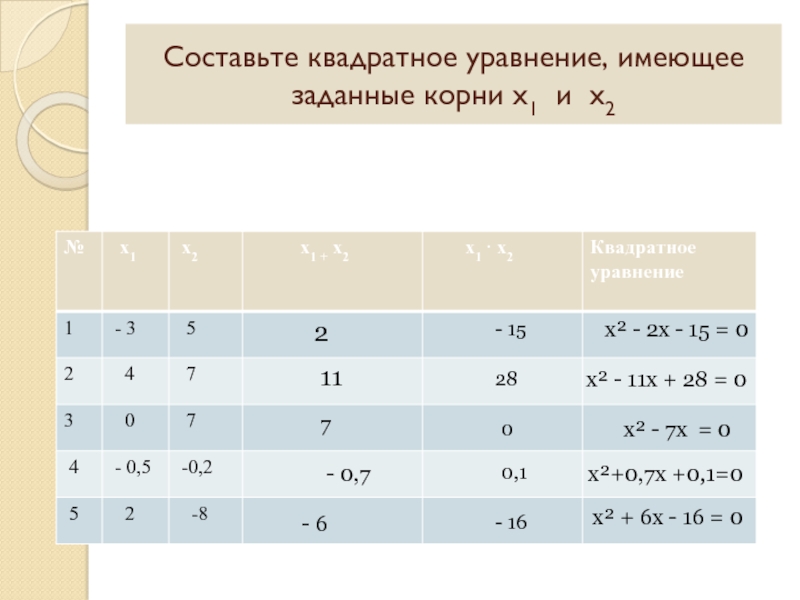
Слайд 26Составьте квадратное уравнение, имеющее заданные корни х1 и х2
2
- 15
11
28
х² - 11х + 28 = 0
7
0
х² - 7х = 0
- 0,7
0,1
х²+0,7х +0,1=0
- 6
- 16
х² + 6х - 16 = 0
Слайд 27ПРИМЕНЕНИЕ ТЕОРЕМЫ
Проверяем, правильно ли найдены корни уравнения.
Определяем знаки корней уравнения не
Устно находим корни приведенного квадратного уравнения.
Составляем квадратное уравнение с заданными корнями.