- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Степени и показательная функция (10 класс)
Содержание
- 1. Презентация по алгебре на тему Степени и показательная функция (10 класс)
- 2. Все, что без этого было
- 3. Слайд 3
- 4. степеньnСтепенью числа а называется произведение n множителей, каждый из которых равен апоказательоснование степениа
- 5. Свойства степени
- 6. Степенная функцияФункция, заданная формулой f (x) =xα называется степенной (с показателем степени α).
- 7. Упростите (А)
- 8. Из истории…
- 9. Области применения
- 10. определение Показательной функцией называется функция вида
- 11. Свойства показательной функции:
- 12. Слайд 12
- 13. Однородные уравнения 9х+6х=22х+1;Используя свойства степени, представим выражения
- 14. Линейные уравненияУкажите промежуток, которому принадлежит корень уравненияВынесем
- 15. Приводимые к квадратномуНайдите сумму корней уравнения:1;
- 16. Показательно - логарифмическое уравнение
- 17. Определение логарифмаЛогарифмом положительного числа b по положительному
- 18. Уравнения, решаемые нестандартными способамиРешить уравнение:Построим в одной
- 19. Решите неравенство:(часть А)Решение: Преобразуем левую и правую
- 20. Применение свойств функцийНайдите область определения функции: Решение.
- 21. Применение производнойНайдите наибольшее значение функции
- 22. С5. решите систему уравнений
- 23. Решите систему уравнений:Найдите значение выражения 7х +
Слайд 1Степени и Показательная функция на ЕГЭ
Выполнила Птушкина Н. А., учитель математики
Слайд 2
Все, что без этого было темно, сомнительно и неверно,
М.В.Ломоносов
Слайд 4
степень
n
Степенью числа а называется произведение n множителей, каждый из которых равен
показатель
основание степени
а
Слайд 6
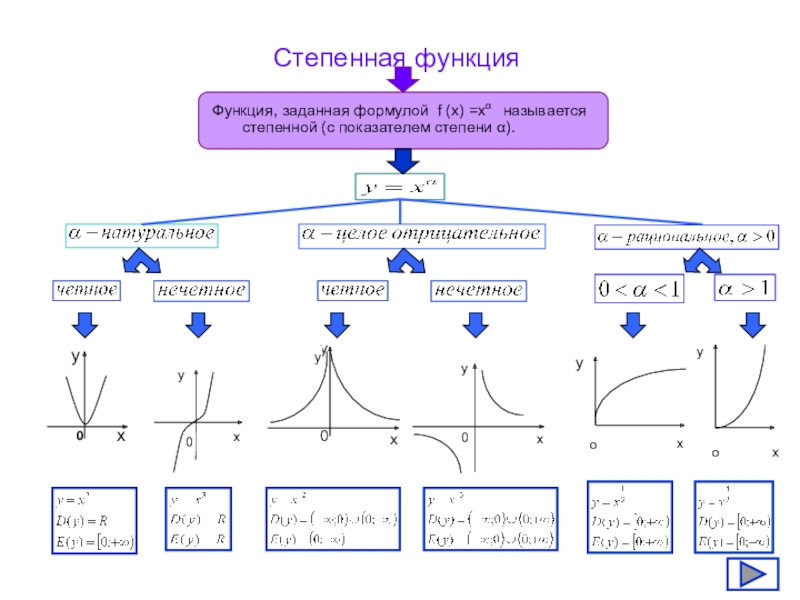
Степенная функция
Функция, заданная формулой f (x) =xα называется степенной (с
Слайд 7Упростите (А)
Воспользуемся свойством
Приведем подобные слагаемые:
Ответ: 4
Выполните действия
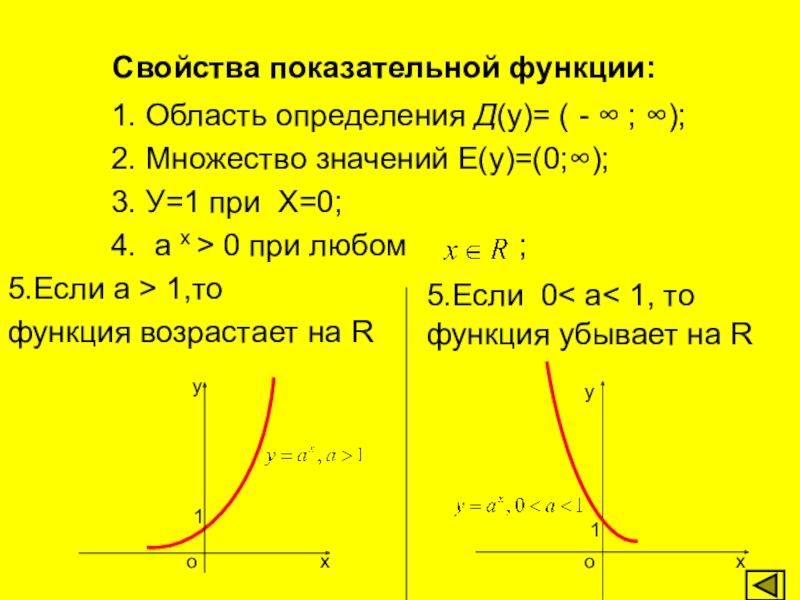
Слайд 11Свойства показательной функции:
1. Область определения
2. Множество значений Е(у)=(0;∞);
3. У=1 при Х=0;
4. а х > 0 при любом ;
5.Если а > 1,то
функция возрастает на R
5.Если 0< а< 1, то
функция убывает на R
Слайд 13Однородные уравнения
9х+6х=22х+1;
Используя свойства степени, представим выражения в виде:
Разделим левую и правую
Пусть
Х=0
Ответ: 0
Слайд 14Линейные уравнения
Укажите промежуток, которому принадлежит корень уравнения
Вынесем степень с наименьшим показателем
х=1
Значит, х=1 (0;2)
Ответ: 4
Слайд 15Приводимые к квадратному
Найдите сумму корней уравнения:
1;
Пусть t=7х, t>0, тогда 49х =(72)х =(7х)2= t2 .
Уравнение примет вид:
49t2 - 50t +1=0,
х1+ х2 =-2 .
Ответ: 3
Слайд 16Показательно - логарифмическое уравнение
По определению логарифма :
Перенесем слагаемое, содержащее
неизвестную, из левой части уравнения
в правую:
Ответ: 1
Слайд 17Определение логарифма
Логарифмом положительного числа b по положительному и отличному от единицы
назад
Слайд 18Уравнения, решаемые нестандартными способами
Решить уравнение:
Построим в одной системе координат графики двух
Функция убывает, а функция
возрастает на (-7;+∞), графики функций пересекаются в одной точке, абсцисса которой равна -2, значит, уравнение имеет единственное решение.
Ответ: -2
у
о
Решение уравнения графическим способом :
Слайд 19Решите неравенство:(часть А)
Решение: Преобразуем левую и правую части
неравенства, учитывая, что
Функция
значит, 3x-7<2,
3x<9,
x<3,
Ответ: 1
Решение: Преобразуем левую и правую части
неравенства, учитывая, что :
Функция возрастает на R,
значит,
Ответ: 2
Слайд 20Применение свойств функций
Найдите область определения функции:
Решение. Числитель и знаменатель дроби
х+4=2;
х=-2.
Итак, данная функция определена при всех значениях х, кроме -2, т.е.верный ответ №4.
Ответ: 4
Укажите функцию, областью значений которой является промежуток (0;+∞).
Решение. Область значений синуса – промежуток [-1;1].
Область значений функции
при четных значениях n – промежуток [0;+∞).
Область значений логарифмической функции – множество всех действительных чисел.
Область значений показательной функции у = ах – промежуток (0;+∞).
Ответ: 4
Слайд 21Применение производной
Найдите наибольшее значение функции
1.Найдем область определения функции: D (y)=(-∞;+∞).
2.Найдем производную функции на области определения:
3.Найдем критические точки функции:
4.Найдем критические точки, принадлежащие отрезку: х=2 [1;3]
5.Найдем значения функции на концах отрезка и в критической точке, принадлежащей отрезку:
У(1)=2,7е-2≈10/27;
У(2)=2,7;
У(3)=2,7е-4≈1/е3;
6.Выберем наибольшее из них: у=2,7.
Ответ: 2,7
Слайд 22
С5. решите систему уравнений
Решение:
Рассмотрим второе уравнение системы.
Возможны два варианта.
равенство
Тогда х+8 = 9 ; х=1, но это значение не входит в ОДЗ первого уравнений.
2) основание равно 1. у - 2 = 1; у=3.
Первое уравнение преобразовывается в
Пусть
Или
Левая часть уравнения возрастающая функция, правая – убывающая.
Значит, существует не более одного решения, которое легко подбирается t=1, х=9.
Ответ: х=9; у=3.
Слайд 23Решите систему уравнений:
Найдите значение выражения 7х + у, если (х; у)
Решение.
Значит, 7х + у = 6.
Ответ: 6