- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Системы двух уравнений с двумя неизвестными(7 класс)
Содержание
- 1. Презентация по алгебре на тему Системы двух уравнений с двумя неизвестными(7 класс)
- 2. Слайд 2
- 3. Повторение:Свойства уравнений:Любой член уравнения можно перенести из
- 4. Решите уравнения:1. 7х-8=4х+73х=15,х=52. 3х=0,18х=0,06Выразите у через ху
- 5. Задача 1: Купили 3 карандаша по х
- 6. Уравнением первой степени с двумя неизвестными х
- 7. Вернёмся к уравнению: 3х + 2у =90Выразим
- 8. 3х + 2у =90 –это первое уравнение.Используя
- 9. Решением системы будет одна пара чисел:х=10, у=30Решением
- 10. Решить систему уравнений – это значит найти
- 11. Способы решения систем уравненийСпособ подстановки2. Способ сложения3. Графический способ
- 12. Способ подстановкиРешить систему уравнений:1. Выразим из одного
- 13. у = 5х-12. Подставим полученное выражение в другое уравнение системы:5х+3(5х-1)=17.Получили уравнение с одним неизвестным. Решим его.5х+15х-3=17,20х-3=17,20х=17+3,20х=20,х=1.
- 14. у = 5х-1,х=13.Подставим найденное значение х в
- 15. Слайд 15
- 16. Способ сложенияРешите систему уравнений:Способ сложения заключается в
- 17. Слайд 17
- 18. Слайд 18
- 19. Графический способ1. Выразим из каждого уравнения у
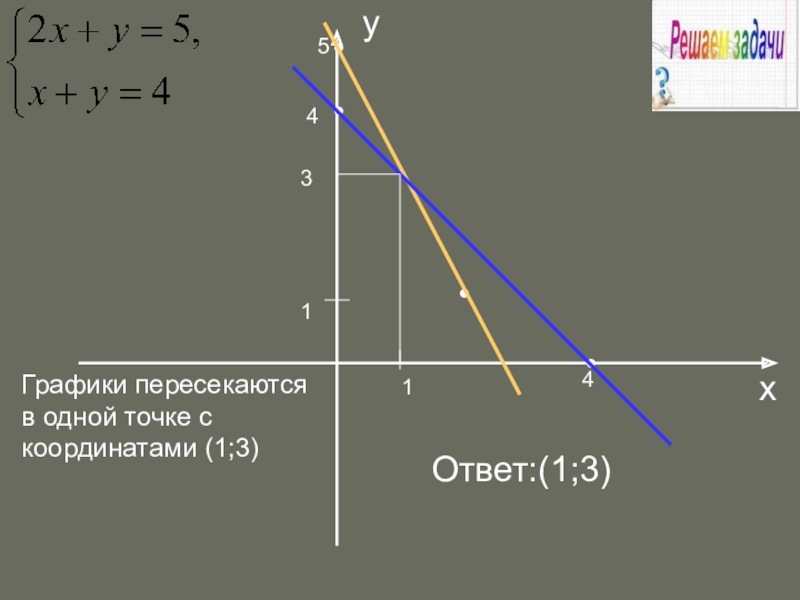
- 20. 11••••3Графики пересекаютсяв одной точке с координатами (1;3)Ответ:(1;3)ху544
- 21. Слайд 21
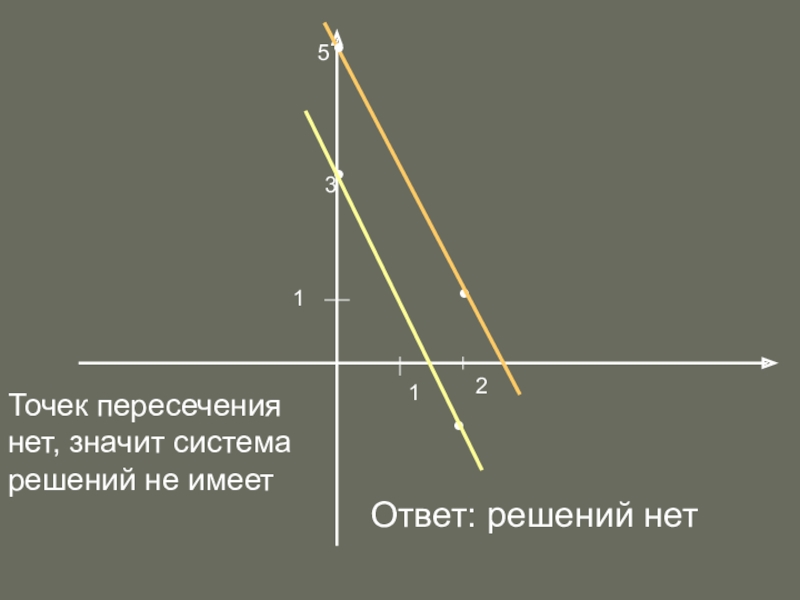
- 22. Решить графически систему уравнений:у=5-2ху=3-2х
- 23. 11•••Точек пересечения нет, значит системарешений не имеетОтвет: решений нет•532
- 24. Решение более сложных систем уравнений:1.Решить систему уравнений:Введём подстановку: Получим систему уравнений:
- 25. Решим систему способом подстановки:Вернёмся к подстановке:m=5-n,3(5-n)+2n=1,15-3n+2n=1,-n=-14,n=14. m=-9,
- 26. Вычислить координаты точки пересечения прямых4х+3у=8 и 3х+2у=6.Решим
- 27. Мы рассмотрели три способа решения систем.Если задуматься
Слайд 3Повторение:
Свойства уравнений:
Любой член уравнения можно перенести из одной части уравнения в
2) Обе части уравнения можно умножить
или разделить на одно и то же число ,
не равное нулю
Слайд 4Решите уравнения:
1. 7х-8=4х+7
3х=15,х=5
2. 3х=0,18
х=0,06
Выразите у через х
у + 4х = 6
у
5х – у =2
у = 5х - 2
Слайд 5Задача 1: Купили 3 карандаша по х рублей
и 2 ручки по
покупку 90 рублей. Сколько стоит карандаш
и сколько стоит ручка?
Составим уравнение: 3х + 2у =90
Подберите вместо х и у такие значения,
чтобы равенство было верным.
х=10,у=30
х=20,у=15
Данное уравнение называется
уравнением первой степени
с двумя неизвестными
Слайд 6Уравнением первой степени с двумя
неизвестными х и у называется уравнение
Решением уравнения с двумя неизвестными
х и у называется упорядоченная пара чисел
(х ;у), при подстановке которых в это
уравнение, получается верное числовое
равенство.
Слайд 7Вернёмся к уравнению: 3х + 2у =90
Выразим у через х,
Задача
Купили 3 карандаша по х рублей
и 2 ручки по у рублей, заплатив за всю
покупку 90 рублей. Сколько стоит карандаш
и сколько стоит ручка, если ручка дороже
карандаша на 20 рублей?
Слайд 83х + 2у =90 –это первое уравнение.
Используя условие, что ручка дороже
Так как в этих уравнениях числа х и у одни
и те же, то эти уравнения рассматривают
совместно и говорят, что они образуют
систему двух уравнений с двумя неизвестными, которую записывают так:
Слайд 9Решением системы будет одна пара чисел:
х=10, у=30
Решением системы двух уравнений с
неизвестными называют такую пару чисел
х и у, которая при подстановке в эту систему
обращает каждое её уравнение в верное
равенство.
Записывается решение так:(х ; у).
Слайд 10Решить систему уравнений – это значит
найти все её решения или
что их нет.
Например, система уравнений
решений не имеет.
Слайд 12Способ подстановки
Решить систему уравнений:
1. Выразим из одного уравнения
( всё равно
у = 5х-1
Слайд 13у = 5х-1
2. Подставим полученное выражение в другое
уравнение системы:
5х+3(5х-1)=17.Получили уравнение
неизвестным. Решим его.
5х+15х-3=17,
20х-3=17,
20х=17+3,
20х=20,
х=1.
Слайд 14у = 5х-1,х=1
3.Подставим найденное значение х в
выражение для у .
у
Ответ: (1;4).
Обратите внимание!
На первом месте всегда записываем х,
на втором у
Слайд 16Способ сложения
Решите систему уравнений:
Способ сложения заключается
в том, что складывая или
уравнения, исключим одно из
неизвестных.
Сложим уравнения: х+у=11
х-у=1,
+
2х=12,
х=6.
Подставим х в любое уравнение системы
6+у=11,у=11-6,у=5. Ответ: (6;5)
Слайд 19Графический способ
1. Выразим из каждого уравнения у через х
у=5-2х, у=4-х
Построим в
графики этих функций
Графиком линейной функции является
прямая. Для построения прямой нужно
две точки, координаты которых даны в таблице
Слайд 24Решение более сложных систем уравнений:
1.Решить систему уравнений:
Введём подстановку:
Получим систему уравнений:
Слайд 25Решим систему способом подстановки:
Вернёмся к подстановке:
m=5-n,
3(5-n)+2n=1,
15-3n+2n=1,
-n=-14,n=14.
m=-9,
Слайд 26Вычислить координаты точки пересечения прямых
4х+3у=8 и 3х+2у=6.
Решим систему уравнений способом сложения:
•2
•3
8х+6у=16,
9х+6у=18
-
-х
х=2.
4•2+3у=8,
3у=0,
у=0.
Ответ: прямые пересекаются
в точке(2;0).
Слайд 27Мы рассмотрели три способа решения систем.
Если задуматься о том, какой из
то ответить на этот вопрос нельзя.
Для каждой конкретной системы выбираем тот
способ, которым именно эту систему решить проще.