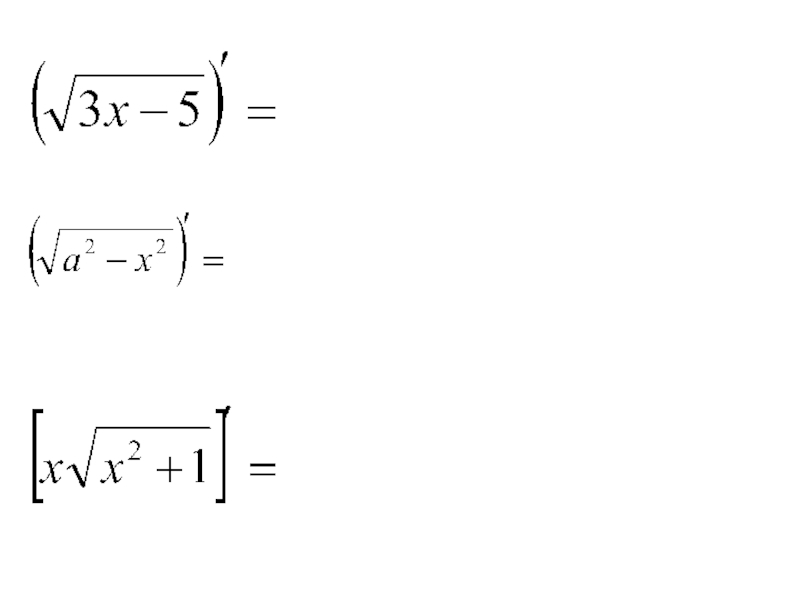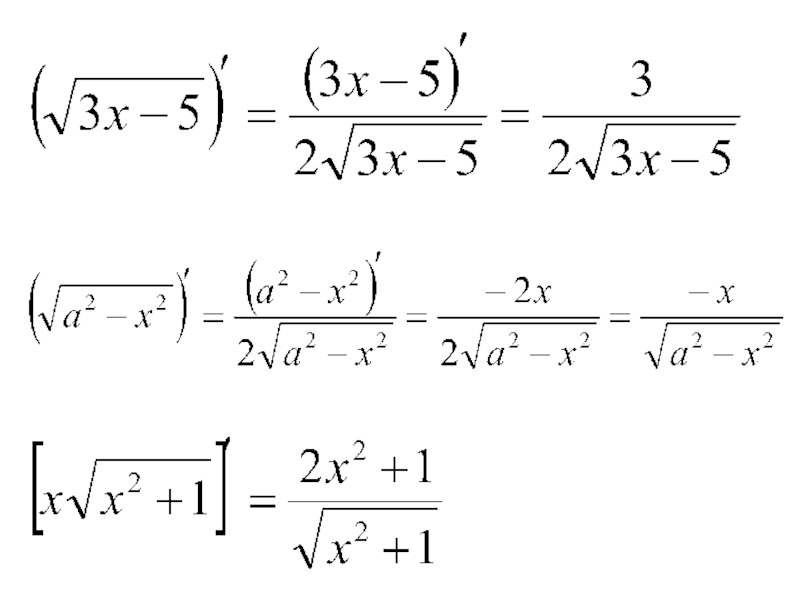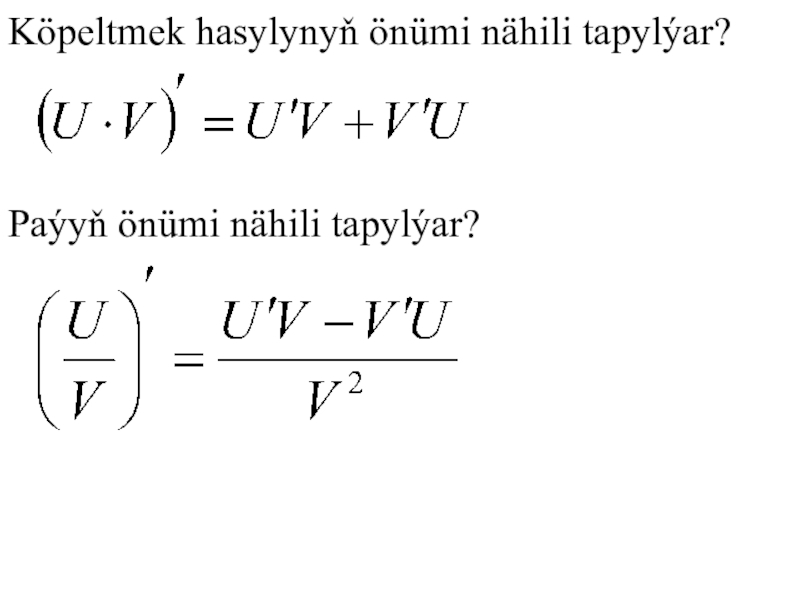- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Производные высших порядков (3 курс пед.училищ) на туркменском языке
Содержание
- 1. Презентация по алгебре на тему Производные высших порядков (3 курс пед.училищ) на туркменском языке
- 2. I.Guramaçylyk döwri
- 3. II.Geçilen temany soramak
- 4. Geçen sapak haýsy temany öwrendik ? Önümiň
- 5. Слайд 5
- 6. Слайд 6
- 7. III.Geçilen temanyny jemlemek
- 8. Köpeltmek hasylynyň önümi nähili tapylýar?Paýyň önümi nähili tapylýar?
- 9. Önümiň predel dilindäki kesgitlemesi aýdyň?Nähili funksiýa çylşyrymly funksiýa diýilýär we onuň önümi nähili tapylýar?
- 10. Galtaşýanyň deňlemesini ýazyň?Egrä geçirilen normalyň deňlemesini ýazyň?
- 11. IV. TÄZE TEMANY DÜŞÜNDIRMEK
- 12. 21.10.2017 ý. Tema: Ýokary tertipli önümler.
- 13. Слайд 13
- 14. Eger funksiýanyň ikinji tertipli önüminden önüm alyp
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Funksivanyň maksimum we minimum nokatlaryna ekstremum nokatlar diýilýär.Funksiýanyň ekstremum nokatlardaky bahalaryna funksiýanyň ekstremumy diýilýär.
- 20. Funksiýanyň önüminiň nola öwrülýän nokatlaryna kritiki nokatlar
- 21. Funksiýanyň ekstremumynyň zerurlyk şerti.Fermanyň teoremasy: Eger x0
- 22. Funksiýanyň ekstremumynyň 1-nji ýeterlik şerti.Teorema: Goý, y=f(x)
- 23. Слайд 23
- 24. V. TÄZE TEMANY BERKITMEK
- 25. 5
- 26. Слайд 26
- 27. MYSALLAR
- 28. № 60. Ýokary tertipli önümleri tapyň.1) y=x5-7x3+3, y(4)=?y′=5x4-21x2;y′′=20x3-42x;y′′′=60x2-42;y(4)=120x;Jogaby: 120x.
- 29. № 74. Funksiýalaryň ekstremumlaryny 1-nji düzgün boýunça
- 30. VI. BAHALANDYRMAK, TÄZE TEMANY, SAPAGY JEMLEMEK
- 31. Слайд 31
- 32. Üstünlik hemraňyz bolsun!
- 33. Interaktiw-multimediýa elektron sapagy taýýarlan:Saryýew Döwran Abdyrahymowiç,Marynyň H.Derýaýew adyndaky Mugallymçylyk mekdebiniň matematika we informatika mugallymy21,10,2017
I.Guramaçylyk döwri
Слайд 4Geçen sapak haýsy temany öwrendik ? Önümiň esasy formulalary, önüm hasaplamaklyga degişli
mysallar işlemek
№ 65 Algebra X.
Слайд 9Önümiň predel dilindäki kesgitlemesi aýdyň?
Nähili funksiýa çylşyrymly funksiýa diýilýär we onuň
önümi nähili tapylýar?
Слайд 1221.10.2017 ý. Tema: Ýokary tertipli önümler. Önümiň üsti bilen funksiýanyň artmagyny we
kemelmegini kesgitlemek, funksiýanyň ekstremumyny hasaplamak.
Слайд 14Eger funksiýanyň ikinji tertipli önüminden önüm alyp bolýan bolsa, onda oňa
üçünji tertipli önüm ýa-da üçünji önüm diýilýär.
Onda n-nji tertipli, ýokary tertipli önüm
y(n)=(y(n-1))′ formula bilen tapylar.
Meselem:
y=ekx funksiýanyň n-nji önümini tapmaly.
y′=(ekx)′=kekx;
y′′=(kekx)′=k2ekx;
y′′′=(k2ekx)′=k3ekx;
....
y(n)=knekx;
Onda n-nji tertipli, ýokary tertipli önüm
y(n)=(y(n-1))′ formula bilen tapylar.
Meselem:
y=ekx funksiýanyň n-nji önümini tapmaly.
y′=(ekx)′=kekx;
y′′=(kekx)′=k2ekx;
y′′′=(k2ekx)′=k3ekx;
....
y(n)=knekx;
Слайд 19Funksivanyň maksimum we minimum nokatlaryna ekstremum nokatlar diýilýär.
Funksiýanyň ekstremum nokatlardaky bahalaryna
funksiýanyň ekstremumy diýilýär.
Слайд 20Funksiýanyň önüminiň nola öwrülýän nokatlaryna kritiki nokatlar diýilýär.
Şeýlelikde, funksiýanyň ekstremumy bar
bolsa, onda ol diňe kritiki nokatlarda bolup biler.
Funksiýanyň ekstremumyny tapmak üçin ekstremumyň bolmagynyň zerurlyk we ýeterlik şertlerini bilmeli.
Funksiýanyň ekstremumyny tapmak üçin ekstremumyň bolmagynyň zerurlyk we ýeterlik şertlerini bilmeli.
Слайд 21Funksiýanyň ekstremumynyň zerurlyk şerti.
Fermanyň teoremasy: Eger x0 y=f(x) funksiýanyň ekstremum nokady
bolup, f′(x0) bar bolsa, onda f′(x0) =0.
Слайд 22Funksiýanyň ekstremumynyň 1-nji ýeterlik şerti.
Teorema: Goý, y=f(x) funksiýa x0 nokatda we
onuň käbir etrabynda üznüksiz we önümi bar bolsa, onda
1) eger f′(x) x0-dan geçende «+» alamatdan «-» öwrülse, onda x0 funksiýanyň maksimum nokady
2) eger f′(x) x0-dan geçende «-» alamatdan «+» öwrülse, onda x0 funksiýanyň minimum nokady
3) alamatyny üýtgetmese funksiýanyň ekstremumy ýok
hasaplanýar.
1) eger f′(x) x0-dan geçende «+» alamatdan «-» öwrülse, onda x0 funksiýanyň maksimum nokady
2) eger f′(x) x0-dan geçende «-» alamatdan «+» öwrülse, onda x0 funksiýanyň minimum nokady
3) alamatyny üýtgetmese funksiýanyň ekstremumy ýok
hasaplanýar.
Слайд 28№ 60. Ýokary tertipli önümleri tapyň.
1) y=x5-7x3+3, y(4)=?
y′=5x4-21x2;
y′′=20x3-42x;
y′′′=60x2-42;
y(4)=120x;
Jogaby: 120x.
Слайд 29№ 74. Funksiýalaryň ekstremumlaryny 1-nji düzgün boýunça tapyň.
2) y=x3+9x-1
3) y=x3+x2-8x+1
№ 75.
Funksiýalaryň ekstremumlaryny 2-nji düzgün boýunça tapyň.
1) y= -x2+4x
1) y= -x2+4x
Слайд 33Interaktiw-multimediýa elektron
sapagy taýýarlan:
Saryýew Döwran Abdyrahymowiç,
Marynyň H.Derýaýew adyndaky Mugallymçylyk mekdebiniň matematika
we informatika mugallymy
21,10,2017
21,10,2017