- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Преобразование квадратичной функции
Содержание
- 1. Презентация по алгебре на тему Преобразование квадратичной функции
- 2. Цель урока: рассмотреть виды преобразований графика квадратичной
- 3. Актуальность: Тема «Квадратичная функция и
- 4. Квадратичной функцией называется функция, которую можно задать
- 5. Заполни пропуски … 1).Функция у = aх2
- 6. Построение графика функцийПостроить в одной системе координат графики функций и сделать выводы:у=х2у=2х2у= х2
- 7. График функции у=2х2 можно получить из параболы
- 8. Построить графики функций в одной системе координат и сделать выводы:у=х2;у=х2+1;у=х2-1.
- 9. ВыводыГрафик функции у=х2+1 – парабола, полученная в
- 10. Преобразования графика квадратичной функции
- 11. Выводы
- 12. График какой функции , изображенной на рисунках
- 13. График какой функции изображенной на
- 14. Слайд 14
- 15. Слайд 15
- 16. Домашнее задание1.Построить
- 17. Список использованной литературы.1. Макарычев Ю.Н.и др. под
- 18. Парабола является одной из ярких
- 19. В повседневной жизни
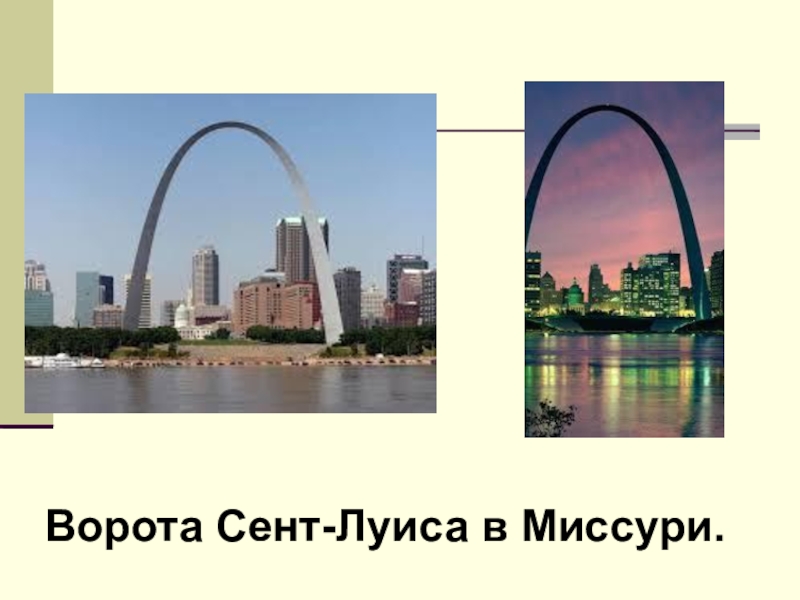
- 20. Ворота Сент-Луиса в Миссури.
- 21. Слайд 21
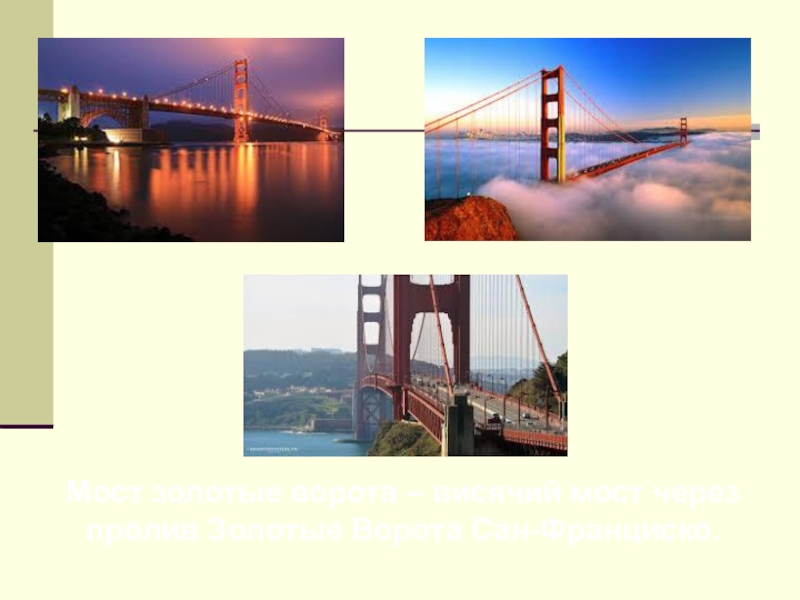
- 22. Мост золотые ворота – висячий мост через пролив Золотые Ворота Сан-Франциско.
- 23. Парабола в архитектуреПамятник оборонного зодчества Киевской Руси периода правления Ярослава Мудрого.
- 24. Парабола в природе
- 25. Спасибо за урок Желаю удачи!!!
Слайд 2Цель урока:
рассмотреть виды преобразований
графика квадратичной функции.
Задачи урока:
•ознакомить учащихся
•научить выполнять преобразования графиков квадратичной функции.
привитие практических умений и навыков по построению графиков.
Слайд 3Актуальность:
Тема «Квадратичная функция и её график» является одной
Слайд 4
Квадратичной функцией называется функция, которую можно задать формулой вида у=ах2, где
Слайд 5Заполни пропуски …
1).Функция у = aх2 где а ≠ 0,
2).График функции у = ах2 при любом а ≠ 0 называют … .
3).Функция у = х2 является … (возрастающей, убывающей) на промежутке х ≤ 0.
4).Значения х, при которых квадратичная функция равна нулю, называют … функции.
…
5).При а >0 ветви параболы у = ах2 направлены … .
6).Если а< о и х ≠ 0, то функция у = ах2 принимает … (положительные, отрицательные) значения.
квадратичной
параболой
убывающей
нулями функции
вверх
отрицательные
Слайд 6Построение графика функций
Построить в одной системе координат графики функций и сделать
у=х2
у=2х2
у= х2
Слайд 7График функции у=2х2 можно получить из параболы у=х2 растяжением вдоль оси
График функции у=1/2х2 можно получить из параболы у=х2 сжатием относительно оси Оу в 2 раза;
Слайд 9Выводы
График функции у=х2+1 – парабола, полученная в результате сдвига графика функции
График функции у=х2+1 – парабола, полученная в результате сдвига графика функции у=х2 на 1 единицу вниз вдоль оси Оу .
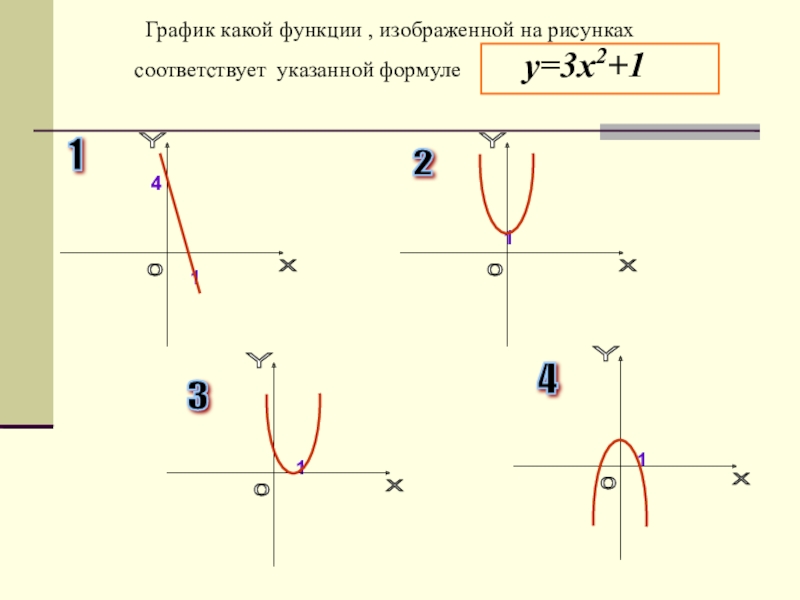
Слайд 12График какой функции , изображенной на рисунках соответствует указанной формуле
4
1
1
1
1
1
2
3
4
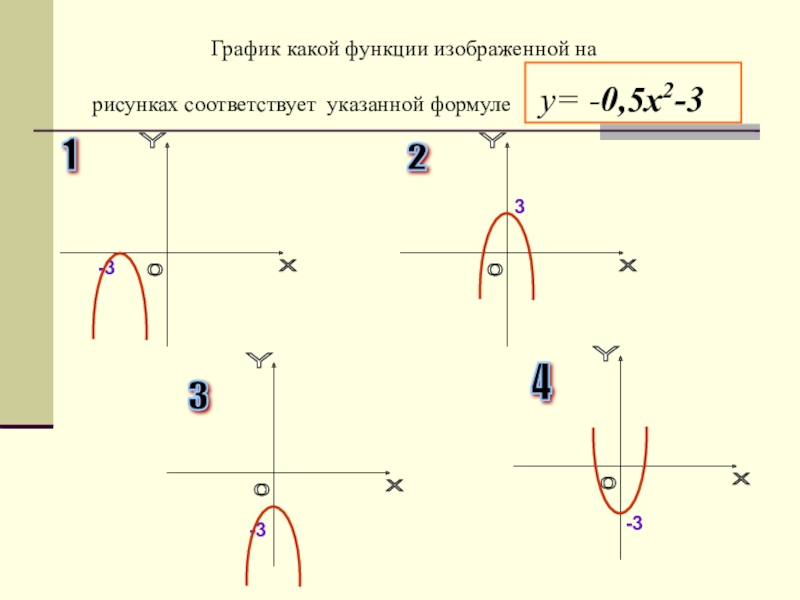
Слайд 13 График какой функции изображенной на рисунках соответствует указанной формуле
-3
-3
3
-3
1
2
3
4
Слайд 14
-
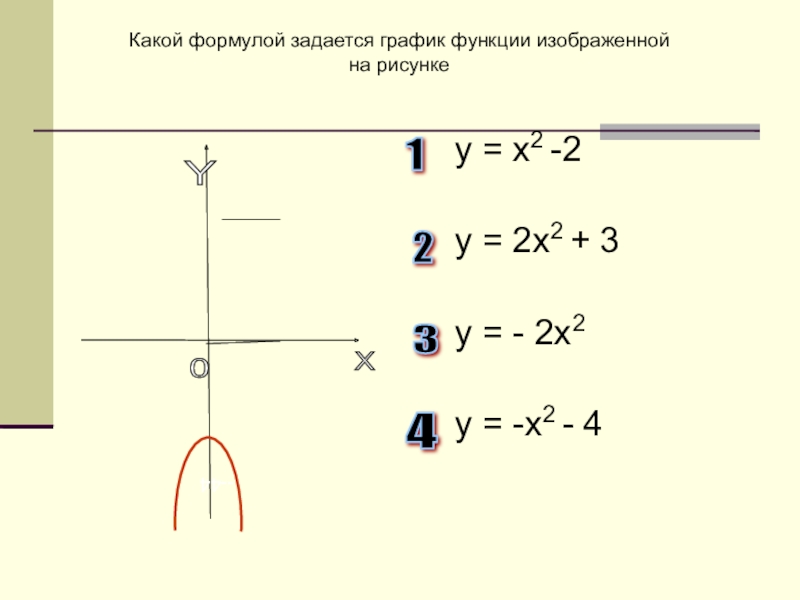
у = х2 -2
у = 2х2 + 3
у = - 2х2
у = -х2 - 4
1
2
3
4
Какой формулой задается график функции изображенной
на рисунке
Слайд 16 Домашнее задание
1.Построить в одной системе координат
а) у=1/2х2 ; б) у=-1/2х2; в) у=1/2х2-2;
г) у=1/2х2 +5
Укажите направление ветвей:
а)y = x2+2; б)y = 2x2-2; в)y = -0,5x2+3.
Слайд 17Список использованной литературы.
1. Макарычев Ю.Н.и др. под редакцией Теляковского С.А. Алгебра
2. А.П.Ершова В.В.Голобородько. Самостоятельные и контрольные работы. Алгебра. Геометрия 9 класс. М.«Илекса», 2010.
3.П.И.Алтынов. Тесты по алгебре. 9 класс. М.«Экзамен», 2012.
Интернет – ресурсы.
www.testent.ru
http://www.uchportal.ru/load/24-1-0-22420
festival.1september.ru/articles/534282/