- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Построение графика квадратичной функции
Содержание
- 1. Презентация по алгебре на тему Построение графика квадратичной функции
- 2. Сформулируйте правило : Как из графика функции у=ах² можно получить график функцииу=ах²+nу=а(х-m)²у=а(х-m)²+n
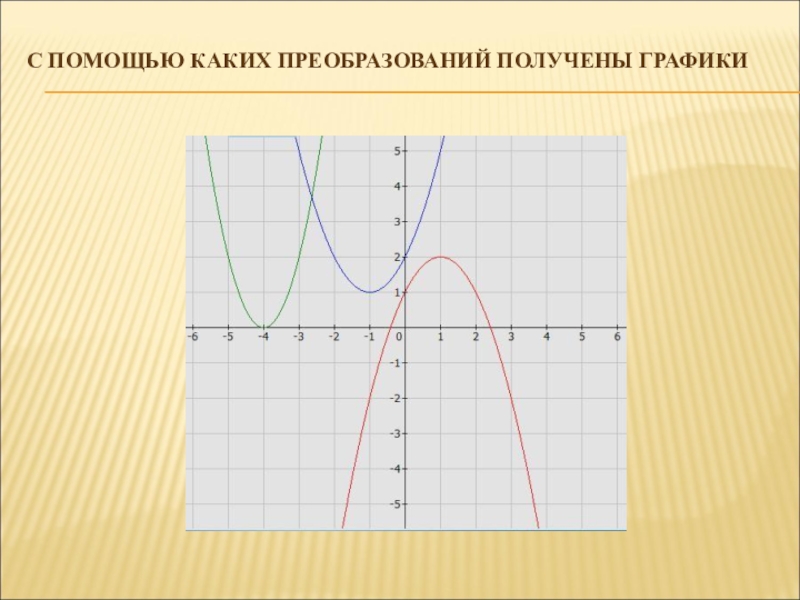
- 3. С ПОМОЩЬЮ КАКИХ ПРЕОБРАЗОВАНИЙ ПОЛУЧЕНЫ ГРАФИКИ
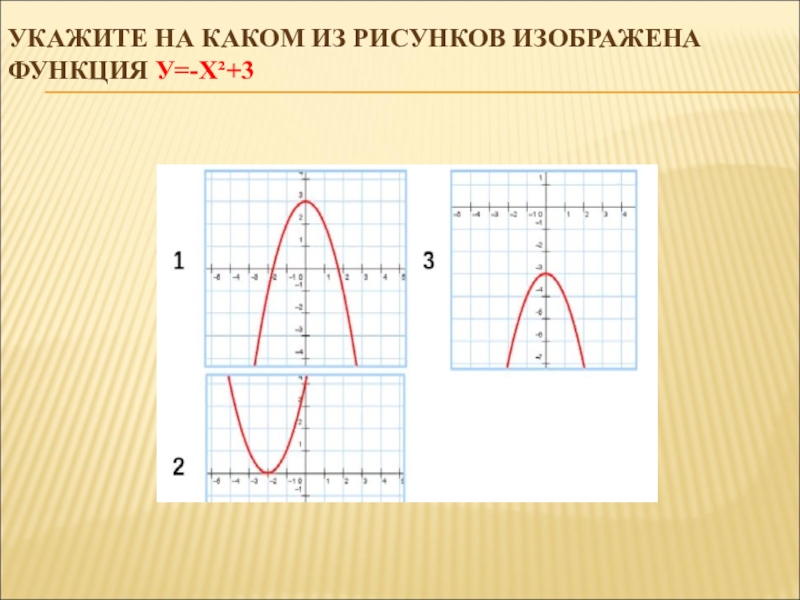
- 4. УКАЖИТЕ НА КАКОМ ИЗ РИСУНКОВ ИЗОБРАЖЕНА ФУНКЦИЯ У=-Х²+3
- 5. УСТАНОВИТЕ СООТВЕТСТВИЕ МЕЖДУ ГРАФИКОМ ФУНКЦИИ, ФОРМУЛОЙ И КООРДИНАТАМИ ВЕРШИНЫ ПАРАБОЛЫ: у =(х+3)² -3у= - 0,5(х-5)²+2у=2(х-з)² +1(5;2)(3;1)(-3;-3)
- 6. ПОСТРОЙТЕ ГРАФИКИ ФУНКЦИЙ, ИСПОЛЬЗУЯ ШАБЛОН ПАРАБОЛЫ:у = х² у = х² -3у =-(х+3)² +2у=х²-10х+28У=-3х²-6х+2
- 7. Построение графика квадратичной функции
- 8. ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:1. Описать функцию:
- 9. ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:ПРИМЕР У=-3Х²-6Х+2(А=-3,B=-6, С=2)НАЙДЕМ
- 10. ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:3. Заполнить таблицу
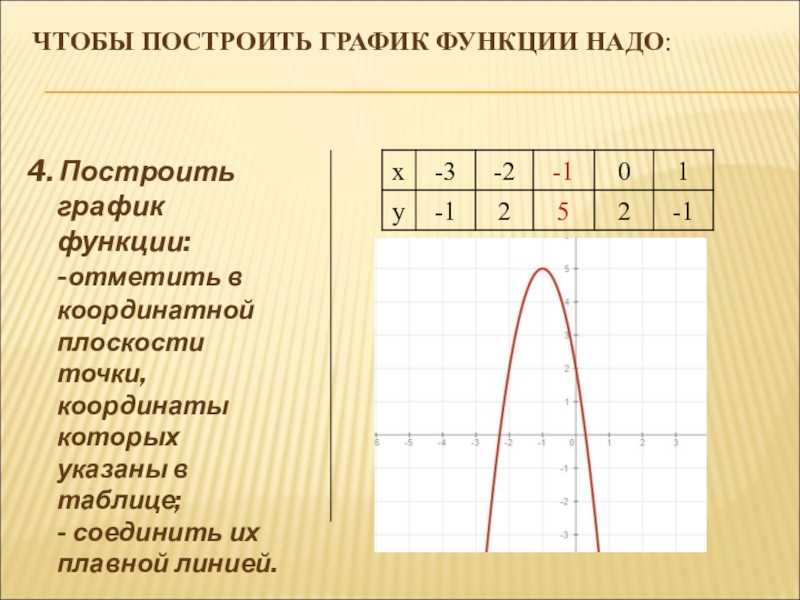
- 11. ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:4. Построить график
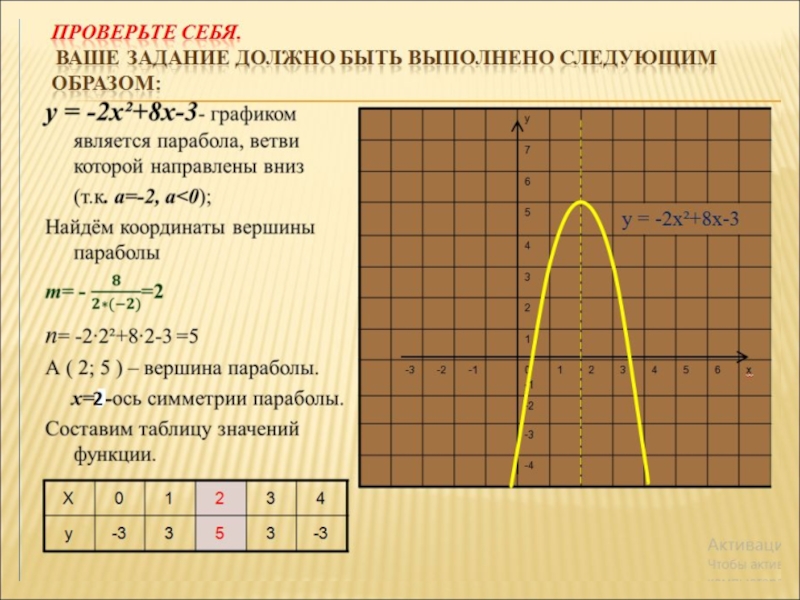
- 12. ПОСТРОЙТЕ ГРАФИК ФУНКЦИИ У = -2Х²+8Х-3. ПЛАН ПОСТРОЕНИЯ:
- 13. Слайд 13
- 14. ДОМАШНЕЕ ЗАДАНИЕ:Пункт №7 упражнение № 121 (а), 125.
- 15. САМОСТОЯТЕЛЬНАЯ РАБОТА. ПОСТРОЙТЕ ГРАФИКИ ФУНКЦИЙ:I варианту = -х²+6х-8II вариант у = -х²-6х-7
- 16. сегодня я узнал… было интересно… было трудно…
- 17. ДРЕВНЯЯ КИТАЙСКАЯ МУДРОСТЬ СКАЖИ МНЕ -
- 18. Спасибо за урок.
Сформулируйте правило : Как из графика функции у=ах² можно получить график функцииу=ах²+nу=а(х-m)²у=а(х-m)²+n
Слайд 2
Сформулируйте правило :
Как из графика функции у=ах² можно
получить график функции
у=ах²+n
у=а(х-m)²
у=а(х-m)²+n
у=ах²+n
у=а(х-m)²
у=а(х-m)²+n
Слайд 5УСТАНОВИТЕ СООТВЕТСТВИЕ МЕЖДУ ГРАФИКОМ ФУНКЦИИ, ФОРМУЛОЙ И КООРДИНАТАМИ ВЕРШИНЫ ПАРАБОЛЫ:
у
=(х+3)² -3
у= - 0,5(х-5)²+2
у=2(х-з)² +1
(5;2)
(3;1)
(-3;-3)
Слайд 6ПОСТРОЙТЕ ГРАФИКИ ФУНКЦИЙ, ИСПОЛЬЗУЯ ШАБЛОН ПАРАБОЛЫ:
у = х²
у = х²
-3
у =-(х+3)² +2
у=х²-10х+28
У=-3х²-6х+2
у =-(х+3)² +2
у=х²-10х+28
У=-3х²-6х+2
Слайд 8ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:
1. Описать функцию:
что является графиком функции
куда
направлены ветви параболы
Пример: у = -3х²-6х+2
графиком является парабола,
ветви которой направлены вниз (т.к. а=-3, а<0)
Слайд 9ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:
ПРИМЕР У=-3Х²-6Х+2
(А=-3,B=-6, С=2)
НАЙДЕМ КООРДИНАТЫ ВЕРШИНЫ ПАРАБОЛЫ
2.Найти координаты
вершины параболы
А(m; n) по формулам
m=-b/2a, n=у(m)
т.е подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить её значение. Прямая х = m является осью симметрии параболы.
А(m; n) по формулам
m=-b/2a, n=у(m)
т.е подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить её значение. Прямая х = m является осью симметрии параболы.
Слайд 10ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:
3. Заполнить таблицу значений функции:
прямая x=m
ось симметрии
Координаты вершины параболы расположить в середине таблицы
посчитать значение функции в выбранных значениях х
Координаты вершины параболы расположить в середине таблицы
посчитать значение функции в выбранных значениях х
Пример: у =-3 х²-6х-+2
А(-1;5) – вершина параболы
х=-1 – ось симметрии параболы.
Составим таблицу значений функции:
Слайд 11ЧТОБЫ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ НАДО:
4. Построить график функции:
-отметить в координатной плоскости точки, координаты которых указаны в таблице; - соединить их плавной линией.
Слайд 15САМОСТОЯТЕЛЬНАЯ РАБОТА.
ПОСТРОЙТЕ ГРАФИКИ ФУНКЦИЙ:
I вариант
у = -х²+6х-8
II вариант
у = -х²-6х-7
Слайд 16сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я
понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
Слайд 17ДРЕВНЯЯ КИТАЙСКАЯ МУДРОСТЬ СКАЖИ МНЕ - И Я ЗАБУДУ, ПОКАЖИ МНЕ - И
Я ЗАПОМНЮ,
ВОВЛЕКИ МЕНЯ – И Я ПОЙМУ