Учитель: Миронова Т.Н.
Дата проведения: 21 ноября 2014г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Показательная функция, ее график и свойства (11 класс)
Содержание
- 1. Презентация по алгебре на тему Показательная функция, ее график и свойства (11 класс)
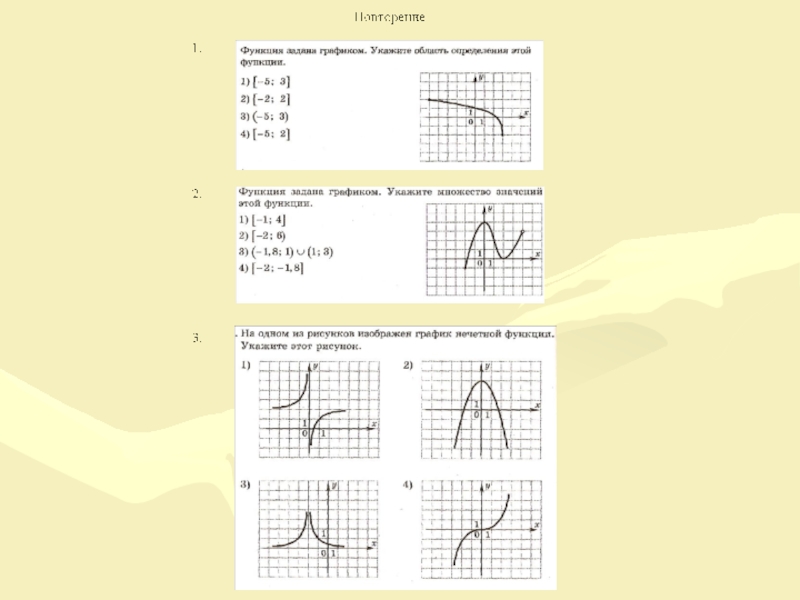
- 2. Повторение (подготовка к итоговой аттестации)
- 3. Слайд 3
- 4. Какие свойства функции вы знаете? Какие преобразования графика функции вы знаете?
- 5. Тема: "Показательная функция, ее свойства и график"
- 6. Построить график функции у = 2хПостроить график функции у = 0,5х
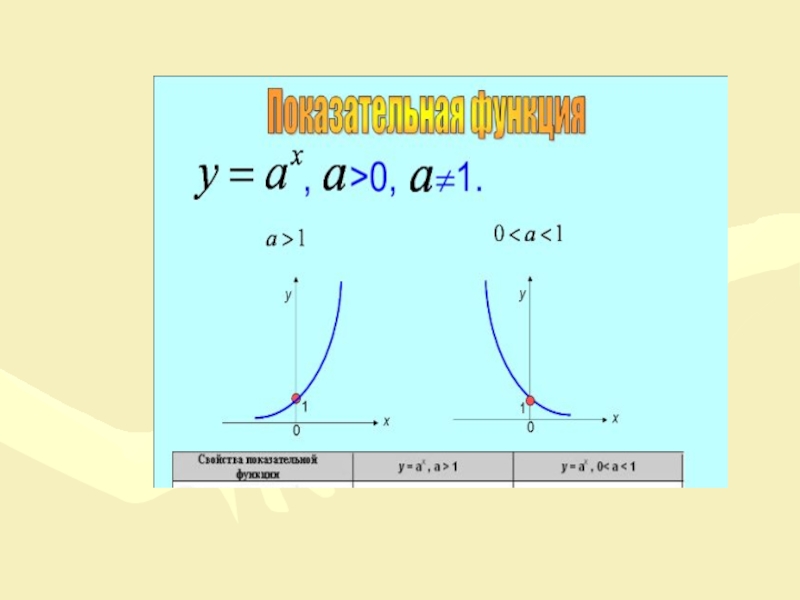
- 7. ОпределениеФункция у = ах, где
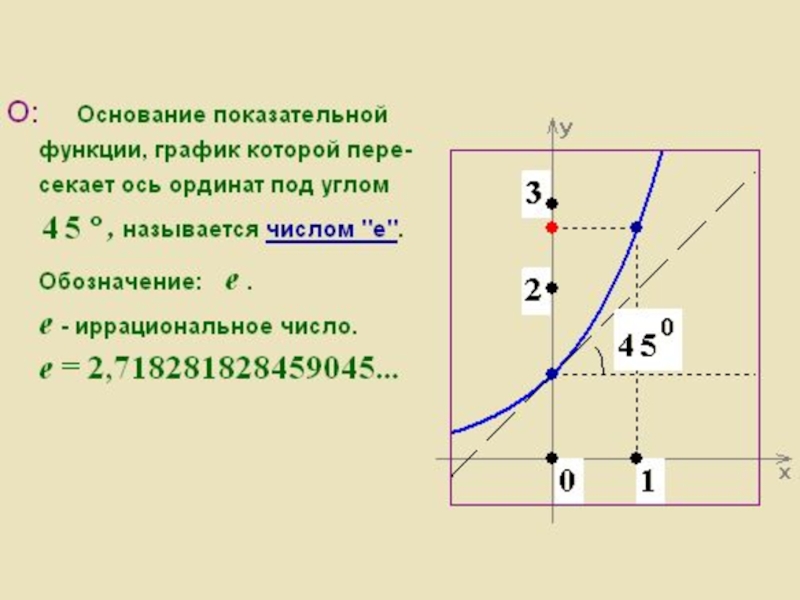
- 8. Слайд 8
- 9. Слайд 9
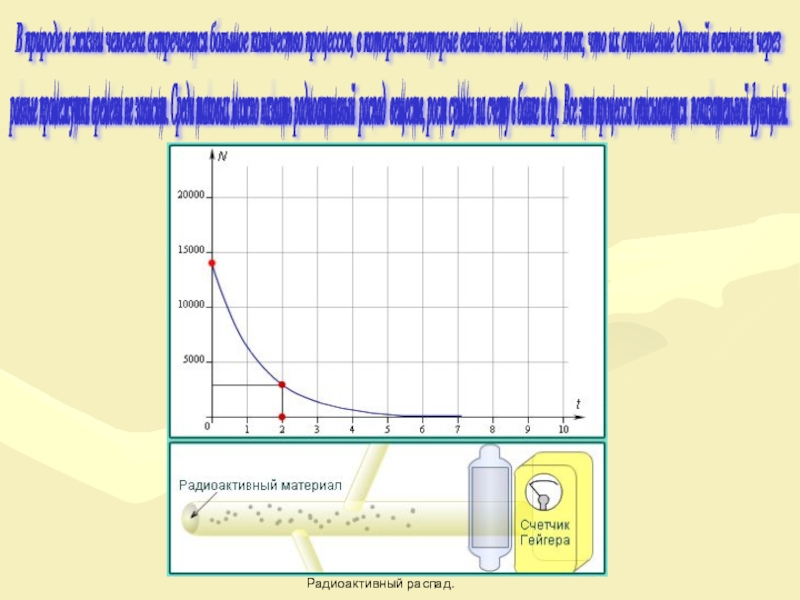
- 10. В природе и жизни человека встречается большое
- 11. Радиоактивный распад описывается формулой m m(t)=m0(½)t/T m(t)
- 12. Слайд 12
- 13. Построение графика функции y=3 и y=(1/3) Свойства показательной функции. x x
- 14. 1. Область определения - множество действительных чисел
- 15. 1. Область определения - множество действительных чисел
- 16. D(y)=(-∞;+∞) E(y)=(0;+∞) 012345-1-2-3-4-5-1-2-3-4-51234567891011x+3 y=(1/3) x-3 y=(1/3) x
- 17. D(y)=(-∞;+∞) E(y)=(-∞;0) 012345-1-2-3-4-5-1-2-3-4-512345678x y=3 x График функции
- 18. Слайд 18
- 19. Слайд 19
- 20. В1. Найти сумму целых значений функции у=-2е +1 на промежутке (-3;3)В2. Построить график функции y=2|x|x
Повторение (подготовка к итоговой аттестации) Решить уравнение4sin2 x – 1 = 0;4cos2 x -1 = 0;Найти корни уравнения на заданном отрезке: 2sin x + =0 [0; 2 ].
Слайд 1Открытый урок в 11 классе по теме: «Показательная функция, ее свойства
и график»
Слайд 2
Повторение
(подготовка к итоговой аттестации)
Решить уравнение
4sin2 x – 1 = 0;
4cos2
x -1 = 0;
Найти корни уравнения на заданном отрезке: 2sin x + =0 [0; 2 ].
Найти корни уравнения на заданном отрезке: 2sin x + =0 [0; 2 ].
Слайд 5Тема: "Показательная функция, ее свойства и график"
Цель: ввести определение показательной
функции и сформулировать её основные свойства; нахождение области определения функции и множество значений функции.
Слайд 7
Определение
Функция у = ах, где а>0 и а
≠ 1 называется показательной, а ее график – экспонентой.
Слайд 10В природе и жизни человека встречается большое количество процессов, в которых
некоторые величины изменяются так, что их отношение данной величины через
равные промежутки времени не зависит. Среди таковых можно назвать радиоактивный распад веществ, рост суммы на счету в банке и др. Все эти процессы описываются показательной функцией.
Радиоактивный распад.
Слайд 11Радиоактивный распад описывается формулой m m(t)=m0(½)t/T
m(t) и m0 – масса
радиоактивного вещества соответственно в момент времени t=0, Т – период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое).
Пример. Период полураспада плутония равен 140 суткам. Сколько плутония останется через 10 лет, если его начальная масса равна 8г?
Решение: Воспользуемся данной формулой. В данной задаче t=10·365 (считаем что в году 365 дней), Т=140. t/Т = 365/14. Ответ: через десять лет плутония останется примерно 1,13·10-7.
Пример. Период полураспада плутония равен 140 суткам. Сколько плутония останется через 10 лет, если его начальная масса равна 8г?
Решение: Воспользуемся данной формулой. В данной задаче t=10·365 (считаем что в году 365 дней), Т=140. t/Т = 365/14. Ответ: через десять лет плутония останется примерно 1,13·10-7.
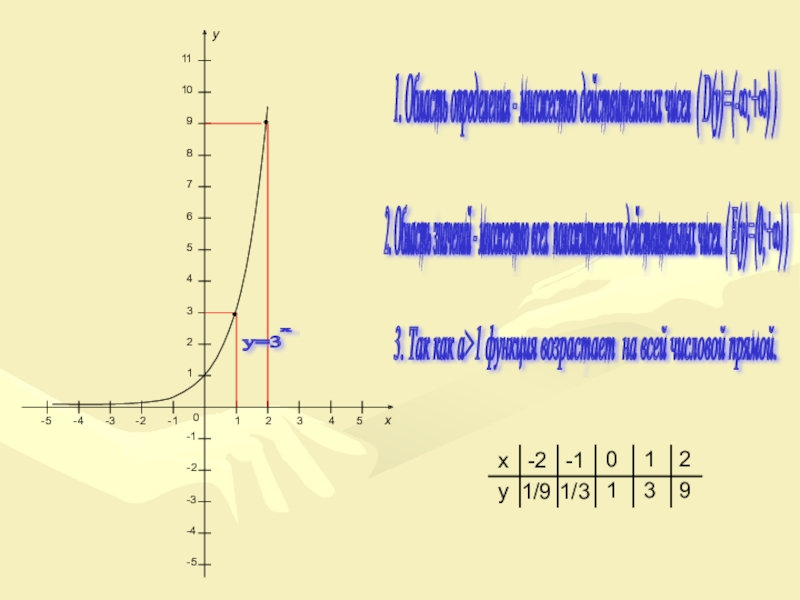
Слайд 141. Область определения - множество действительных чисел ( D(y)=(-∞;+∞) )
2.
Область значений - множество всех положительных действительных чисел. ( E(y)=(0;+∞) )
3. Так как a>1 функция возрастает на всей числовой прямой.
0
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
x
x
y
-2
-1
0
1
2
1/9
1/3
1
3
9
x
y
y=3
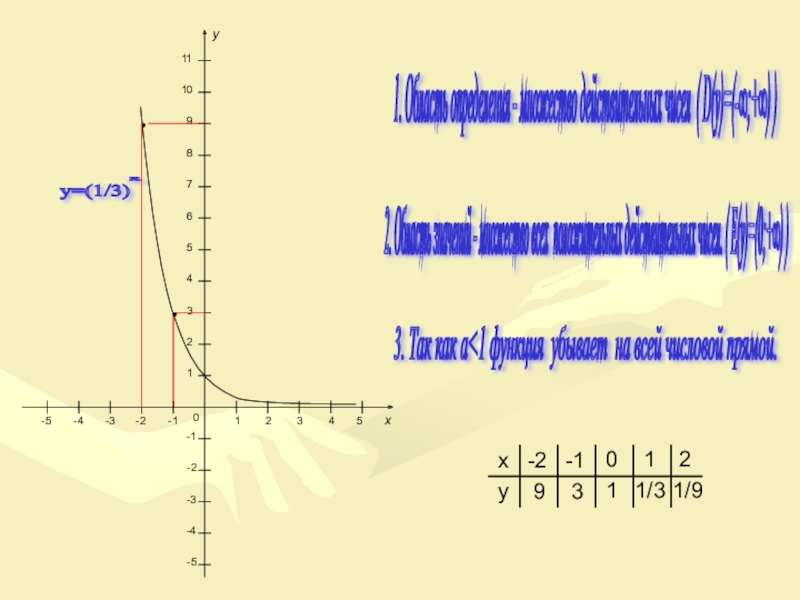
Слайд 151. Область определения - множество действительных чисел ( D(y)=(-∞;+∞) )
2.
Область значений - множество всех положительных действительных чисел. ( E(y)=(0;+∞) )
3. Так как a<1 функция убывает на всей числовой прямой.
0
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
x
y=(1/3)
x
y
-2
-1
0
1
2
9
3
1
1/3
1/9
x
y
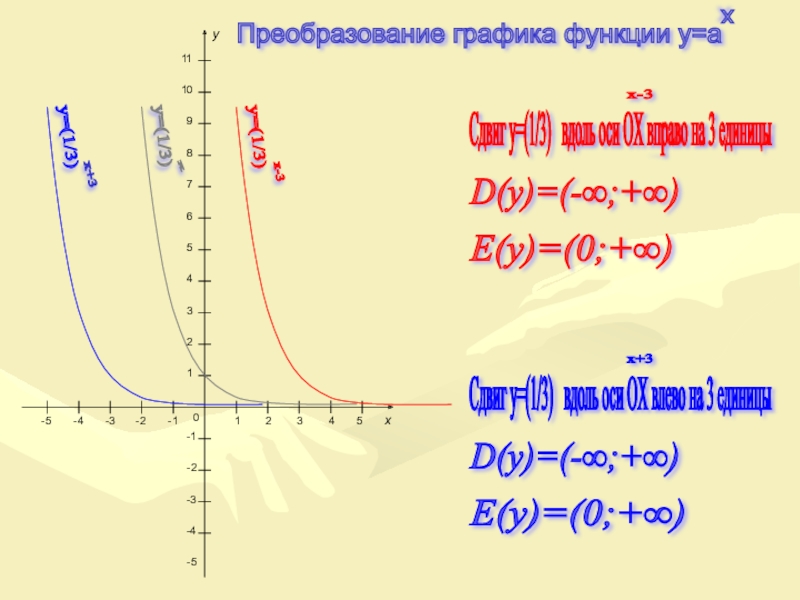
Слайд 16D(y)=(-∞;+∞)
E(y)=(0;+∞)
0
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
x+3
y=(1/3)
x-3
y=(1/3)
x
y=(1/3)
x-3
Сдвиг y=(1/3)
вдоль оси OX вправо на 3 единицы
D(y)=(-∞;+∞)
E(y)=(0;+∞)
x+3
Сдвиг y=(1/3) вдоль оси OX влево на 3 единицы
Преобразование графика функции y=a
x
x
y
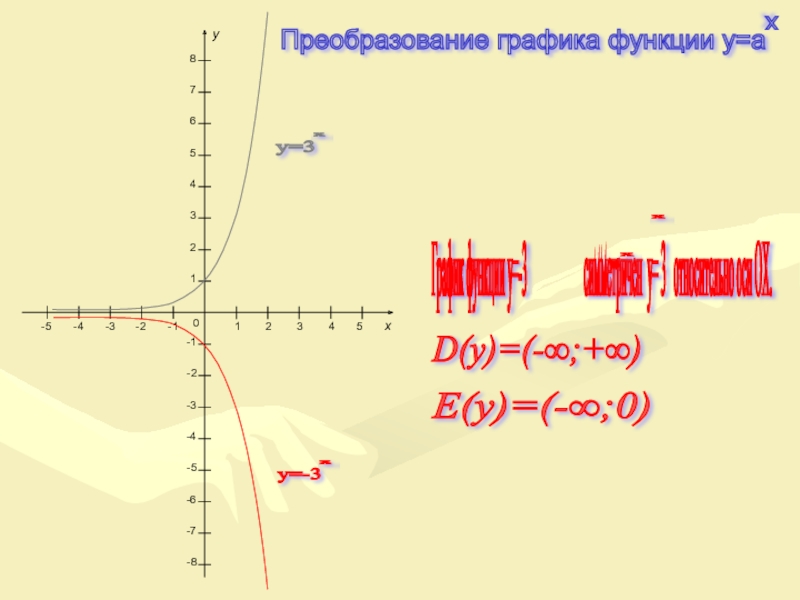
Слайд 17D(y)=(-∞;+∞)
E(y)=(-∞;0)
0
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
x
y=3
x
График функции y=-3
симметричен у= 3 относительно оси OX.
-6
-7
-8
x
y=-3
Преобразование графика функции y=a
x
x
y
x
Слайд 20В1. Найти сумму целых значений функции у=-2е +1 на промежутке (-3;3)
В2.
Построить график функции y=2
|x|
x
