- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Перестановки
Содержание
- 1. Презентация по алгебре на тему Перестановки
- 2. 1) Сколькими способами можно расставить 3 различные
- 3. В магазине "Все для чая" есть 5
- 4. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0; 1 и 2?
- 5. При встрече 4 школьника обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
- 6. Проверка теста
- 7. Слайд 7
- 8. Пусть имеются три книги. Обозначим их
- 9. Слайд 9
- 10. Пусть мы имеем n элементов. На
- 11. Слайд 11
- 12. Сколько трёхсловных предложений можно составить из трёх слов: сегодня, солнце, светит?
- 13. Слайд 13
- 14. Задачи на закрепление пройденного материала.Сколькими способами могут
- 15. Поиграем! В течение 1 минуты составьте как
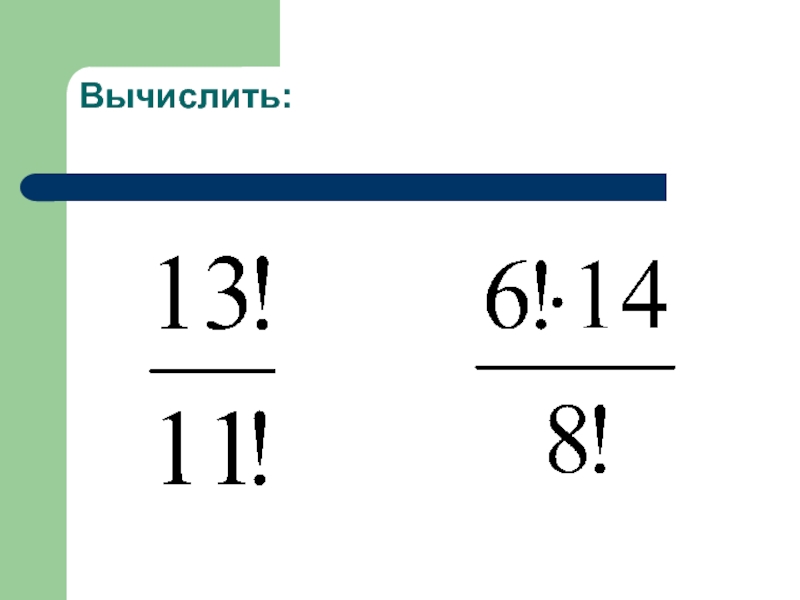
- 16. Вычислить:
1) Сколькими способами можно расставить 3 различные книги на книжной полке?а) 12 б) 6 в) 9 г)
Слайд 2
1) Сколькими способами можно расставить 3 различные книги на книжной полке?
а)
12 б) 6 в) 9 г) 4
Слайд 3
В магазине "Все для чая" есть 5 разных чашек и 3
разных блюдца. Сколькими способами можно купить чашку с блюдцем?
Слайд 7
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Определение
Слайд 8 Пусть имеются три книги. Обозначим их буквами a, b и с.
Эти книги можно расставить на полке по-разному.
Если первой поставить книгу a, то возможны такие расположения книг: abc, acb.
Если первой поставить книгу b, то возможными являются такие расположения: bac, bca.
И наконец, если первой поставить книгу с, то получим такие расположения: cab, cba.
Каждое из этих расположений называют
перестановкой из трёх элементов.
Пример.
Слайд 9 Определение Перестановкой из n элементов называется каждое расположение этих элементов
в определённом порядке.
Число перестановок из n элементов обозначают символом
(читается «Р из n»).
Слайд 10 Пусть мы имеем n элементов.
На первое место можно поставить
любой из них.
Для каждого выбора первого элемента на второе место можно поставить один из оставшихся n-1 элементов.
Для каждого выбора первых двух элементов на третье место можно поставить один из оставшихся
n-2 элементов и т.д.
В результате получим, что
Рn= n (n - 1) ( n – 2) …3·2·1= n!
(читается «n факториал»).
Например, 2!= 2·1=2; 5!=5·4·3·2·1=120.
По определению считают, что 1!=1.
Для каждого выбора первого элемента на второе место можно поставить один из оставшихся n-1 элементов.
Для каждого выбора первых двух элементов на третье место можно поставить один из оставшихся
n-2 элементов и т.д.
В результате получим, что
Рn= n (n - 1) ( n – 2) …3·2·1= n!
(читается «n факториал»).
Например, 2!= 2·1=2; 5!=5·4·3·2·1=120.
По определению считают, что 1!=1.
Слайд 11 Таким образом, число всевозможных перестановок из n элементов вычисляется по
формуле:
= n!= 1·2·3·…·(n-2)(n-1)n
Слайд 14Задачи на закрепление пройденного материала.
Сколькими способами могут встать в очередь в
билетную кассу: 1) 3 человека; 2) 5 человек?
Сколько существует вариантов рассаживания вокруг стола: 1) 6 гостей на 6 стульях; 2) 7 гостей на 7 стульях?
Сколькими способами можно с помощью букв K, L, M и N обозначить вершины четырехугольника?
Сколько различных пятизначных чисел, все цифры которых различны, можно записать с помощью цифр 4, 5, 6, 7 и 8?
Сколькими способами можно расставить на полке 8 книг, среди которых 2 книги одного автора, которые при любых перестановках должны стоять рядом?
В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом?
Сколько существует вариантов рассаживания вокруг стола: 1) 6 гостей на 6 стульях; 2) 7 гостей на 7 стульях?
Сколькими способами можно с помощью букв K, L, M и N обозначить вершины четырехугольника?
Сколько различных пятизначных чисел, все цифры которых различны, можно записать с помощью цифр 4, 5, 6, 7 и 8?
Сколькими способами можно расставить на полке 8 книг, среди которых 2 книги одного автора, которые при любых перестановках должны стоять рядом?
В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом?
Слайд 15Поиграем!
В течение 1 минуты составьте как можно больше слов, состоящих из
букв слова КОМБИНАТОРИКА
Ком, комбинат, комбинатор, тор, рот, банк, банка, кот, ток, рота, тина, тон, нота, каток, мина, бином, мот, том, икра, мир,…