- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Математическая игра по теме Производная
Содержание
- 1. Презентация по алгебре на тему Математическая игра по теме Производная
- 2. Ум заключается не только в знании,
- 3. Правила игры:Каждый играет за себяОтветы записываются в
- 4. Производные элементарных функций:
- 5. Правила вычисления производных:
- 6. Геометрический смысл производной:угловой коэффициент касательной равен f '(x0)Уравнение касательной:Механический смысл производной:
- 7. Слайд 7
- 8. Признаки минимума и максимума функции:если в точке
- 9. 1323130292345672889101112131415161735ИТОИТОГ18192021222324253426273633
- 10. 1.Функция у = f(x) определена на отрезке
- 11. ОТВЕТ: 42. На рисунке изображен график функции
- 12. 3.Функция у = f(x) определена на отрезке
- 13. ОТВЕТ: М 4. На рисунке изображён график
- 14. 5.На рисунке изображен график производной функции у
- 15. 6. На рисунке изображен график y=f/(x)- производной
- 16. ОТВЕТ: К 8. На рисунке изображён график
- 17. ОТВЕТ: 0,5 9. Прямая y=7x-5 параллельна касательной к графику функции y=x2+6x-8. Найдите абсциссу точки касания.
- 18. 10.На рисунке изображен график производной функции у
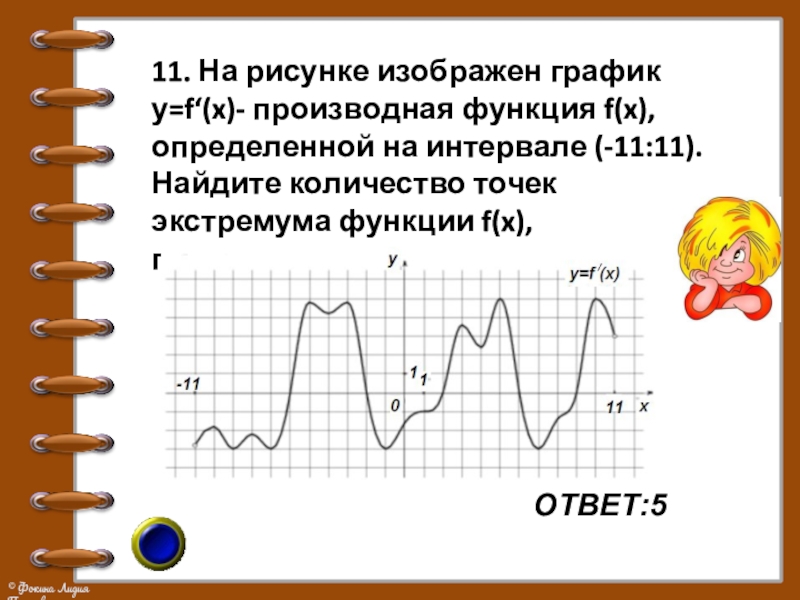
- 19. ОТВЕТ:5 11. На рисунке изображен график у=f‘(x)-
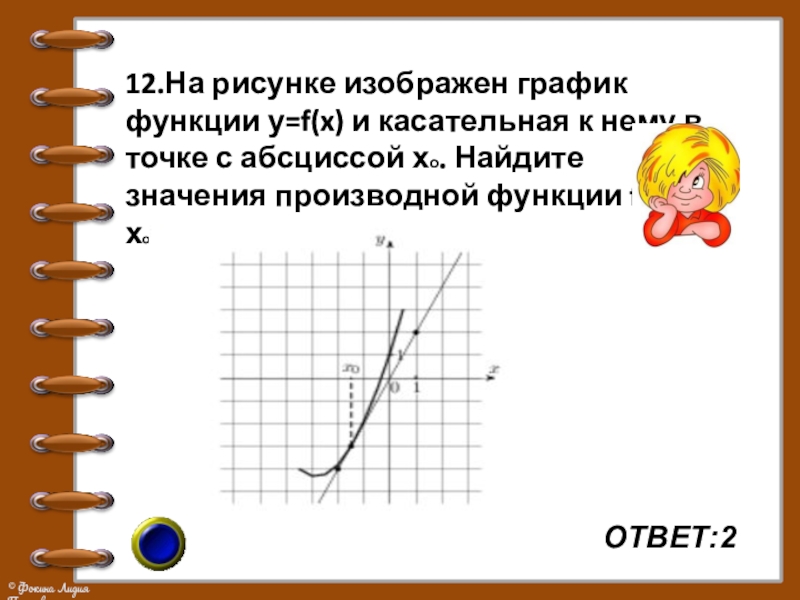
- 20. ОТВЕТ:2 12.На рисунке изображен график функции у=f(x)
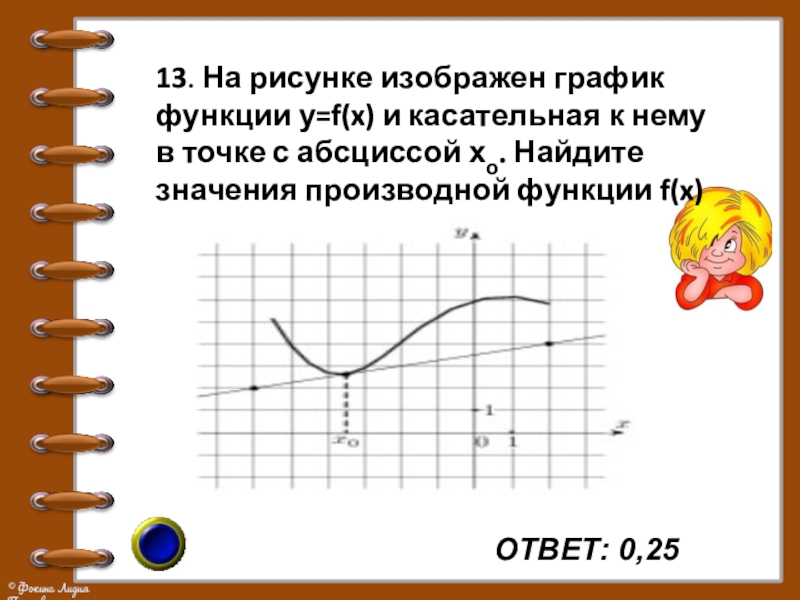
- 21. 13. На рисунке изображен график функции у=f(x)
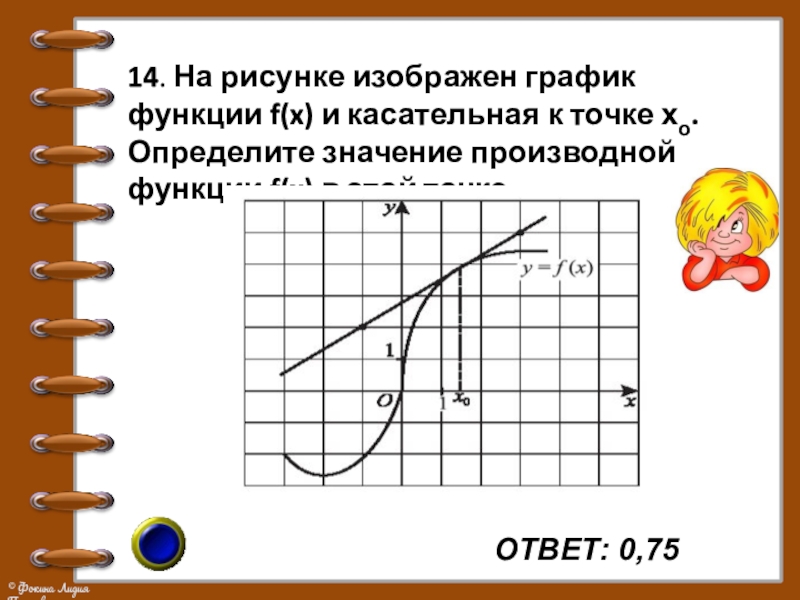
- 22. ОТВЕТ: 0,75 14. На рисунке изображен график
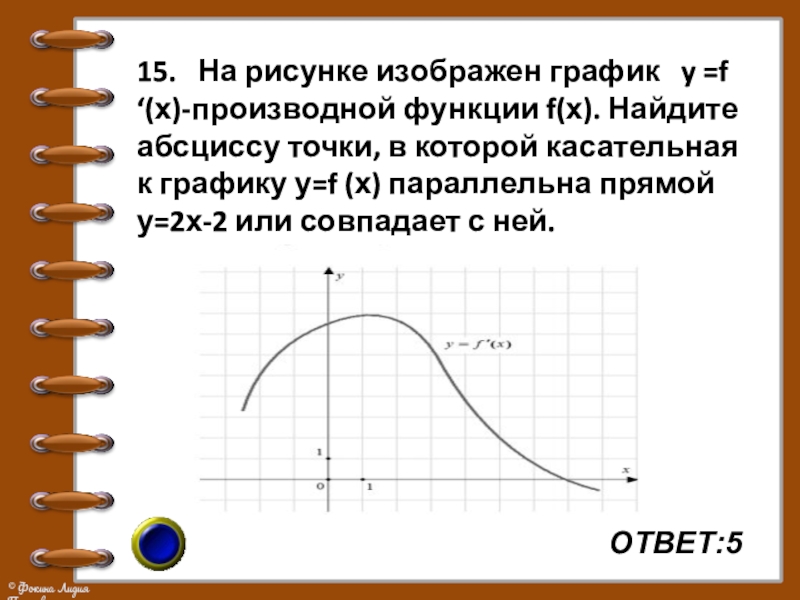
- 23. ОТВЕТ:5 15. На рисунке изображен график
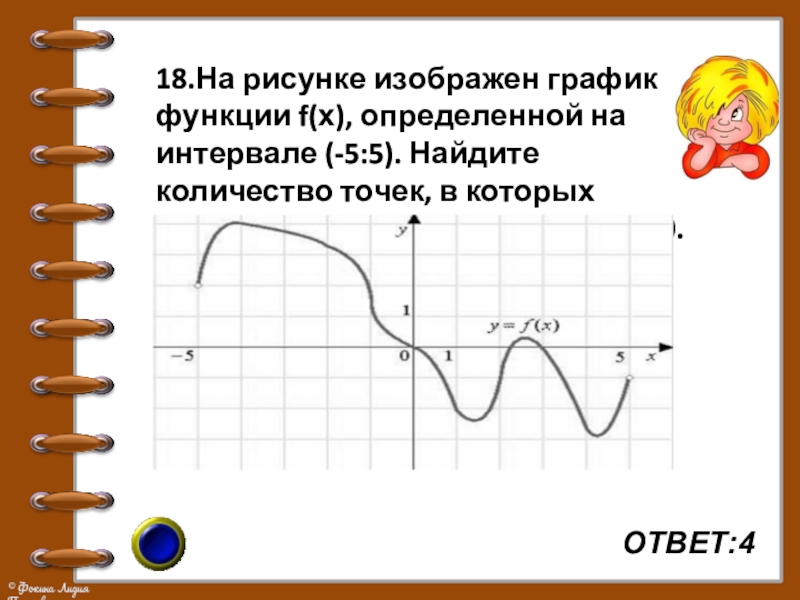
- 24. ОТВЕТ:418.На рисунке изображен график функции f(х), определенной
- 25. ОТВЕТ: 6019. Материальная точка движется прямолинейно по
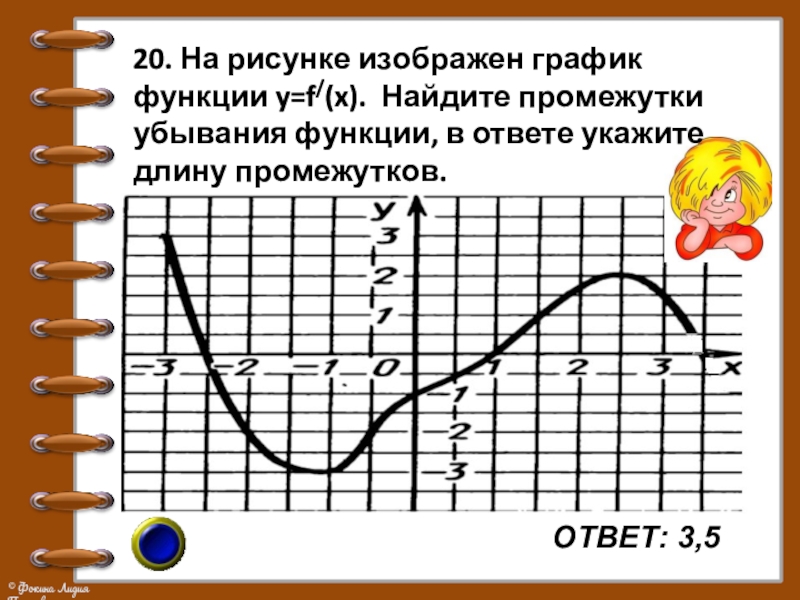
- 26. 20. На рисунке изображен график функции y=f/(x).
- 27. ОТВЕТ:59 21. Материальная точка движется прямолинейно по
- 28. ОТВЕТ: 822. Материальная точка движется прямолинейно по
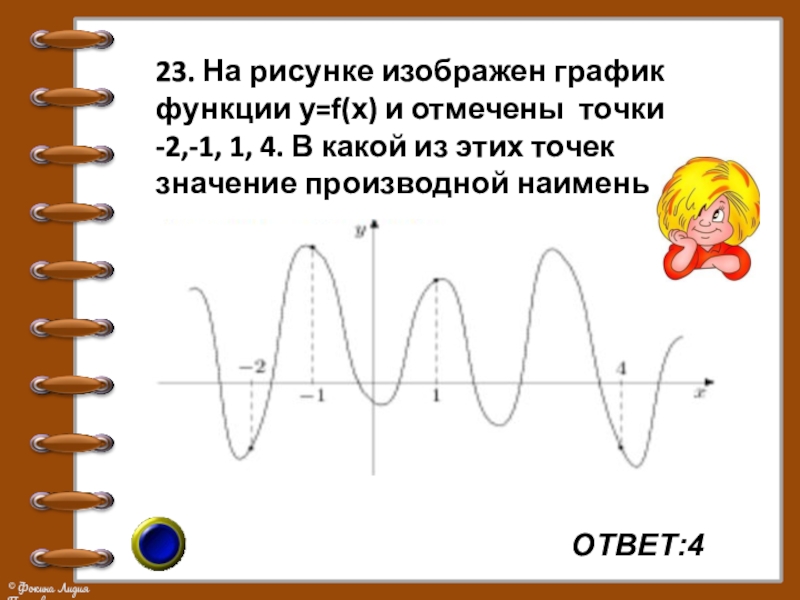
- 29. ОТВЕТ:4 23. На рисунке изображен график функции
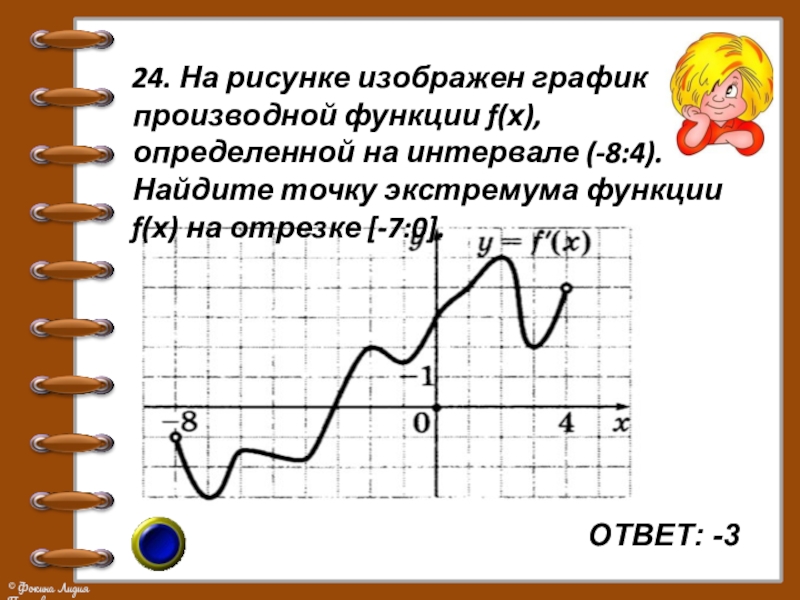
- 30. ОТВЕТ: -324. На рисунке изображен график производной
- 31. 25. На рисунке изображен график функции y=f(x)
- 32. 26. На рисунке изображен график функции у=
- 33. ОТВЕТ: D 27. На рисунке изображён график
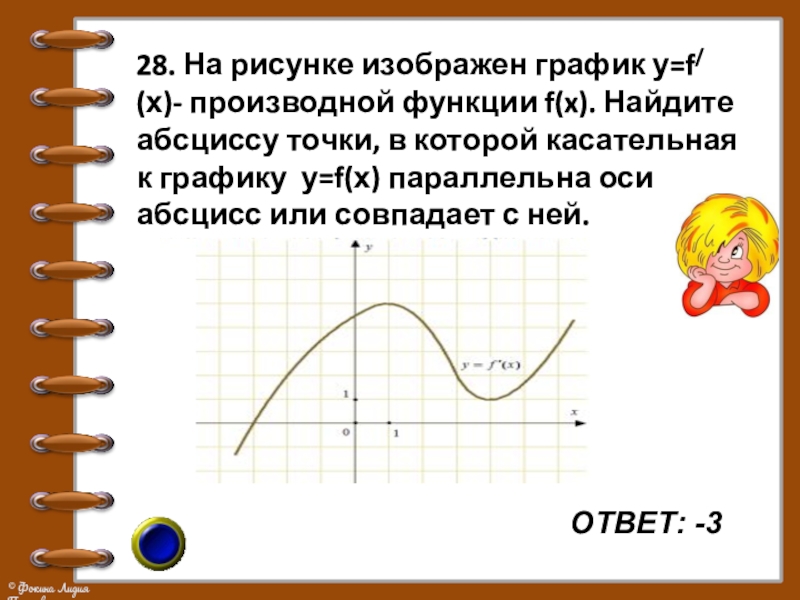
- 34. ОТВЕТ: -3 28. На рисунке изображен график
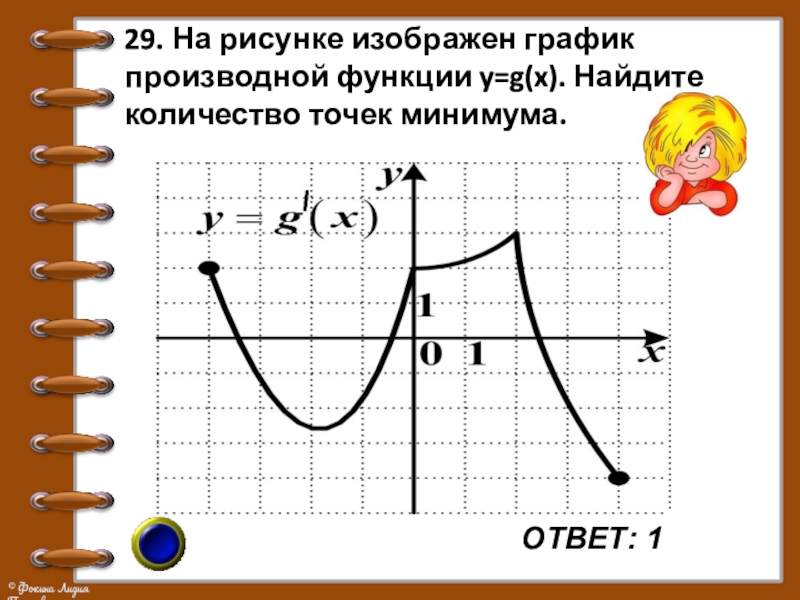
- 35. ОТВЕТ: 129. На рисунке изображен график производной функции y=g(x). Найдите количество точек минимума.
- 36. 31. Найдите промежутки, на которых производная функции положительна. ОТВЕТ: [-4;-3] и [-2;0]
- 37. ОТВЕТ: -13 32. Вычислите значение производной функции f(x)= 3x2-x+5 в точке x=-2.
- 38. ОТВЕТ: 4 33. На рисунке изображен график
- 39. ОТВЕТ: 2 35. На рисунке изображен график
- 40. 36. На рисунке изображен график функции у=f(x)
- 41. Вы – счастливчик!!! Вы получаете + 2 балла
- 42. Вам повезло!!!Вы получаете +1 балл
- 43. Супер!!!Вам придется расстаться с 1 баллом
- 44. Подведём итоги!
Ум заключается не только в знании, но и в умении применять знания на практике.
Слайд 1Математическая игра по теме «ПРОИЗВОДНАЯ».
Государственное бюджетное профессиональное образовательное учреждение
«Брянский профессионально-педагогический колледж»
Слайд 3Правила игры:
Каждый играет за себя
Ответы записываются в бланке ответов
За правильно решенное
задание –1 балл
Задания выбирают по очереди
Выигрывает тот, кто наберет больше всего баллов
Задания выбирают по очереди
Выигрывает тот, кто наберет больше всего баллов
Слайд 6Геометрический смысл производной:
угловой коэффициент касательной равен f '(x0)
Уравнение касательной:
Механический смысл производной:
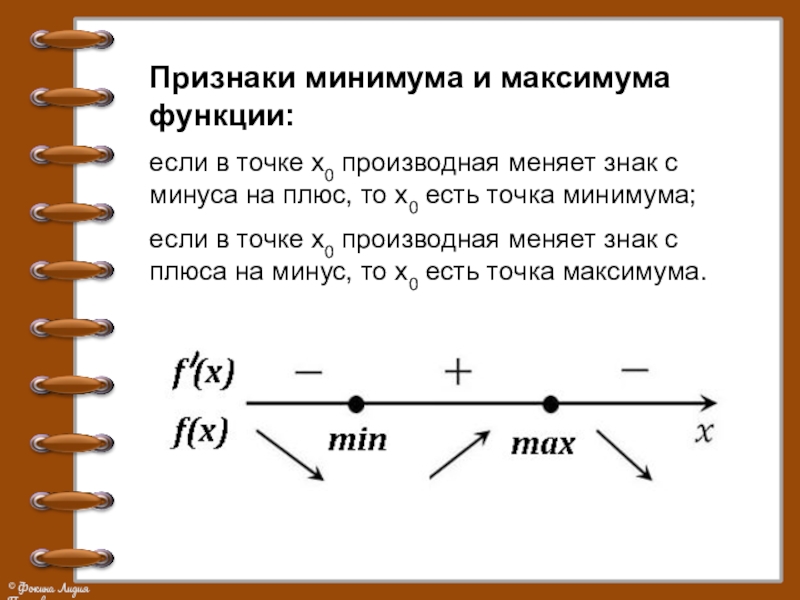
Слайд 8Признаки минимума и максимума функции:
если в точке х0 производная меняет знак
с минуса на плюс, то х0 есть точка минимума;
если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.
если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.
Слайд 101.Функция у = f(x) определена на отрезке [-6; 6]. На рисунке
изображен ее график. Укажите число промежутков, на которых функция у = f'(х) отрицательна .
ОТВЕТ: 4
![1.Функция у = f(x) определена на отрезке [-6; 6]. На рисунке изображен ее график. Укажите число промежутков,](/img/thumbs/63480ed5291384aca6240c59b2e7cb49-800x.jpg "Презентация по алгебре на тему Математическая игра по теме Производная 1.Функция у = f(x) определена на отрезке [-6; 6]. На рисунке")
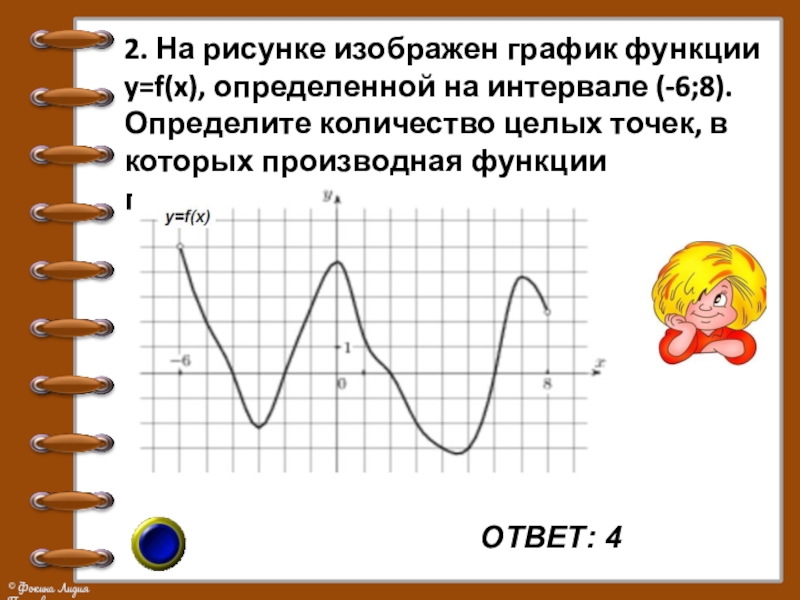
Слайд 11ОТВЕТ: 4
2. На рисунке изображен график функции y=f(x), определенной на интервале
(-6;8). Определите количество целых точек, в которых производная функции положительна.
Слайд 123.Функция у = f(x) определена на отрезке [-6; 6]. На рисунке
изображен график её производной. Укажите число промежутков, на которых функция у = f(x) убывает.
ОТВЕТ: 3
![3.Функция у = f(x) определена на отрезке [-6; 6]. На рисунке изображен график её производной. Укажите](/img/thumbs/0d84e997e49946b4769f1d81b4fe3f03-800x.jpg "Презентация по алгебре на тему Математическая игра по теме Производная 3.Функция у = f(x) определена на отрезке [-6; 6]. На рисунке")
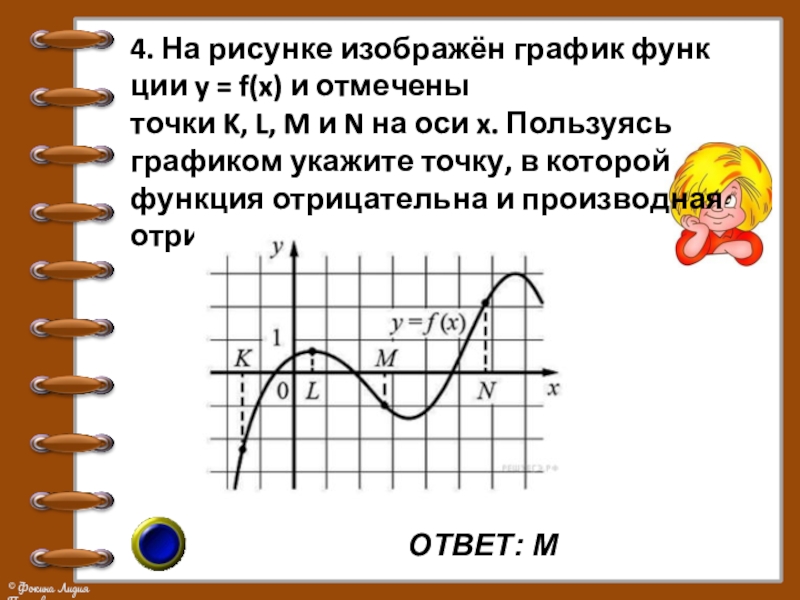
Слайд 13ОТВЕТ: М
4. На рисунке изображён график функции y = f(x) и отмечены точки K, L, M и N на оси x.
Пользуясь графиком укажите точку, в которой функция отрицательна и производная отрицательна.
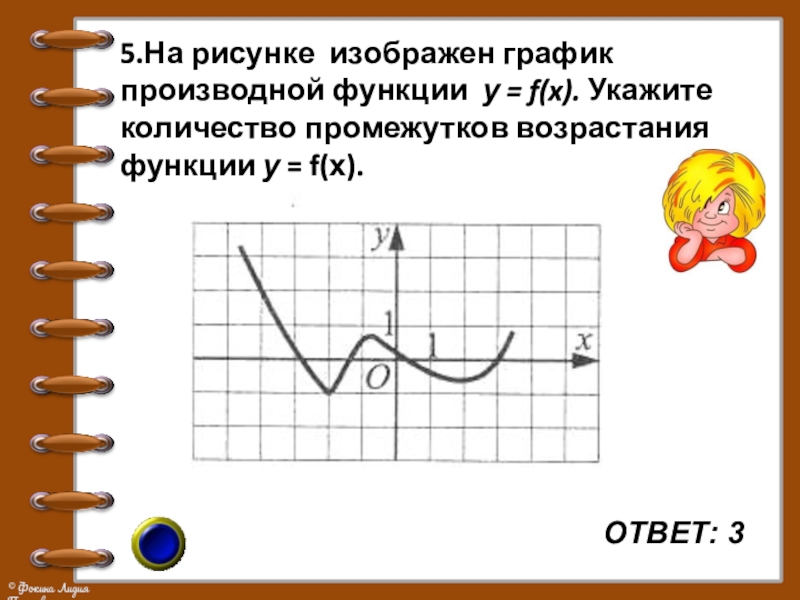
Слайд 145.На рисунке изображен график производной функции у = f(x). Укажите количество
промежутков возрастания функции у = f(х).
ОТВЕТ: 3
Слайд 15
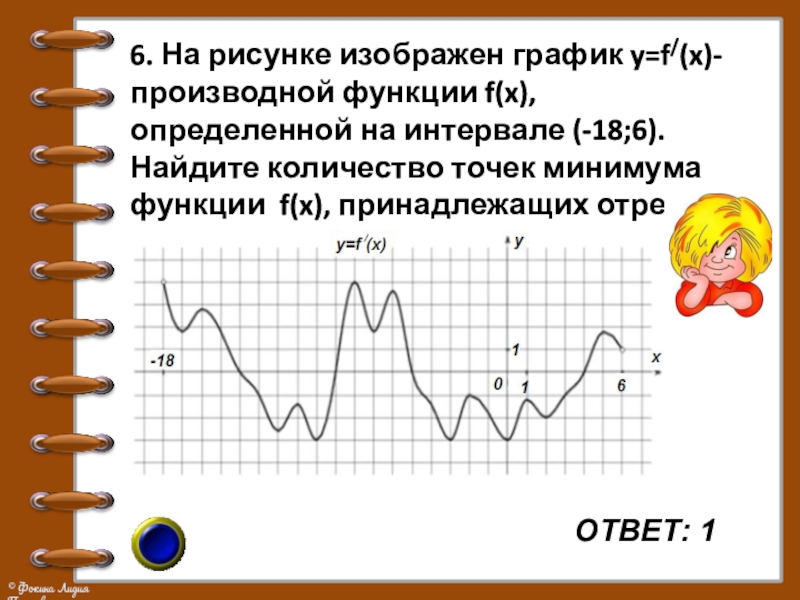
6. На рисунке изображен график y=f/(x)- производной функции f(x), определенной на
интервале (-18;6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].
ОТВЕТ: 1
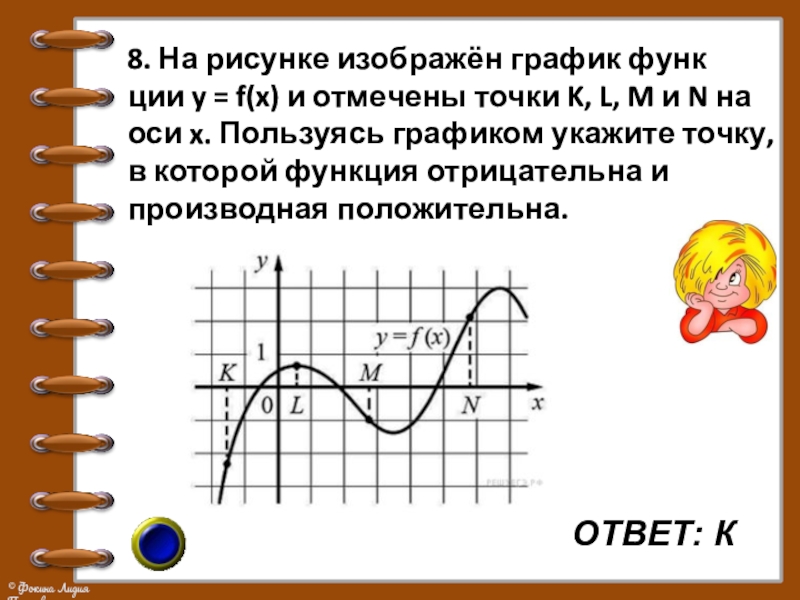
Слайд 16ОТВЕТ: К
8. На рисунке изображён график функции y = f(x) и отмечены точки K, L, M и N на оси x.
Пользуясь графиком укажите точку, в которой функция отрицательна и производная положительна.
Слайд 17ОТВЕТ: 0,5
9. Прямая y=7x-5 параллельна касательной к графику функции y=x2+6x-8.
Найдите абсциссу точки касания.
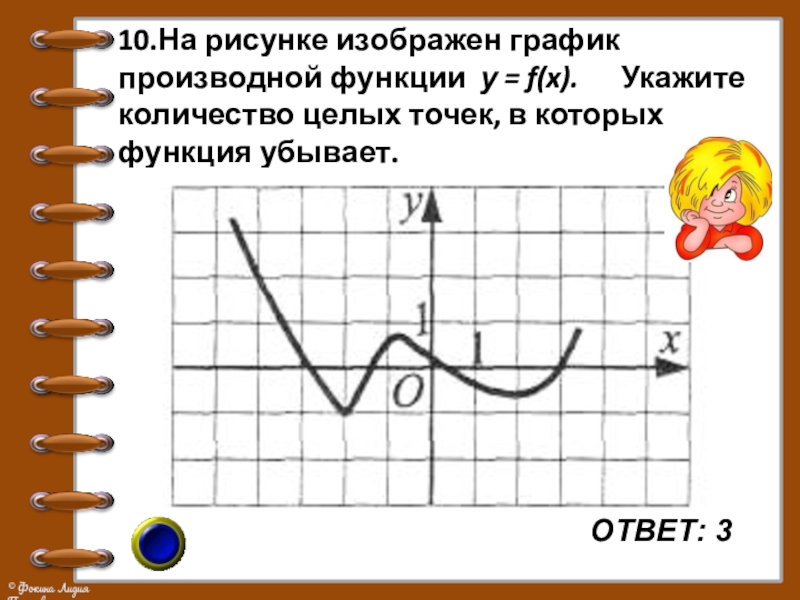
Слайд 1810.На рисунке изображен график производной функции у = f(x).
Укажите количество целых точек, в которых функция убывает.
ОТВЕТ: 3
Слайд 19ОТВЕТ:5
11. На рисунке изображен график у=f‘(x)- производная функция f(x),определенной на
интервале (-11:11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10:10].
Слайд 20ОТВЕТ:2
12.На рисунке изображен график функции у=f(x) и касательная к нему
в точке с абсциссой хо. Найдите значения производной функции f(x) в хо
Слайд 21
13. На рисунке изображен график функции у=f(x) и касательная к нему
в точке с абсциссой хо. Найдите значения производной функции f(x) в хо.
ОТВЕТ: 0,25
Слайд 22ОТВЕТ: 0,75
14. На рисунке изображен график функции f(x) и касательная
к точке хо. Определите значение производной функции f(x) в этой точке.
Слайд 23ОТВЕТ:5
15. На рисунке изображен график y =f ‘(х)-производной
функции f(х). Найдите абсциссу точки, в которой касательная к графику у=f (х) параллельна прямой у=2х-2 или совпадает с ней.
Слайд 24ОТВЕТ:4
18.На рисунке изображен график функции f(х), определенной на интервале (-5:5). Найдите
количество точек, в которых производная функции f(х) равна 0.
Слайд 25ОТВЕТ: 60
19. Материальная точка движется прямолинейно по закону
х(t)=6t2-48t+17, где х-
расстояние от точки отсчета в метрах, t- время в секундах,
измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9с.
измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9с.
Слайд 26
20. На рисунке изображен график функции y=f/(x). Найдите промежутки убывания функции,
в ответе укажите длину промежутков.
ОТВЕТ: 3,5
Слайд 27ОТВЕТ:59
21. Материальная точка движется прямолинейно по закону
х(t)=-t4-6t3+5t=23,где х- расстояние
от точки отсчета в метрах, t- время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=3c .
Слайд 28ОТВЕТ: 8
22. Материальная точка движется прямолинейно по закону
х(t)=t2-13t+23, где х-
расстояние от точки отсчета в метрах, t- время в секундах , измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Слайд 29ОТВЕТ:4
23. На рисунке изображен график функции у=f(х) и отмечены точки
-2,-1, 1, 4. В какой из этих точек значение производной наименьшее?
Слайд 30ОТВЕТ: -3
24. На рисунке изображен график производной функции f(х), определенной на
интервале (-8:4). Найдите точку экстремума функции f(х) на отрезке [-7:0].
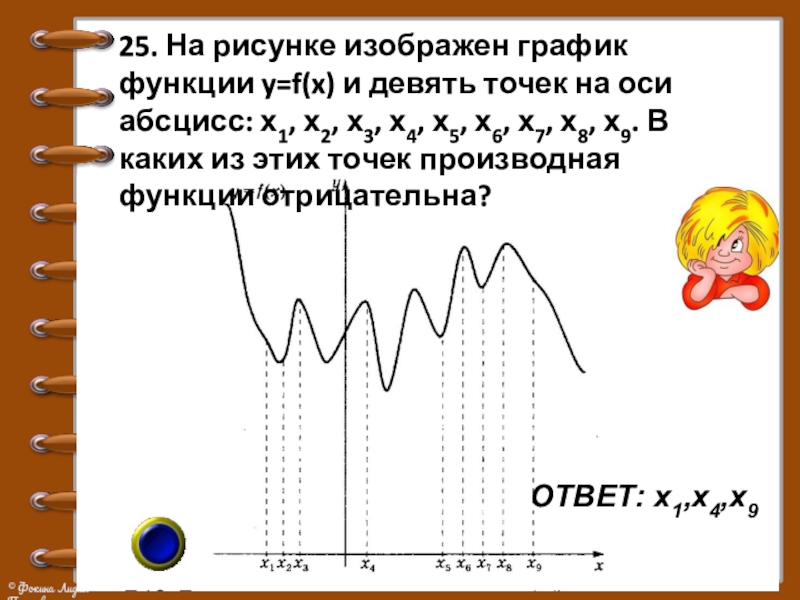
Слайд 3125. На рисунке изображен график функции y=f(x) и девять точек на
оси абсцисс: х1, х2, х3, х4, х5, х6, х7, х8, х9. В каких из этих точек производная функции отрицательна?
ОТВЕТ: х1,х4,х9
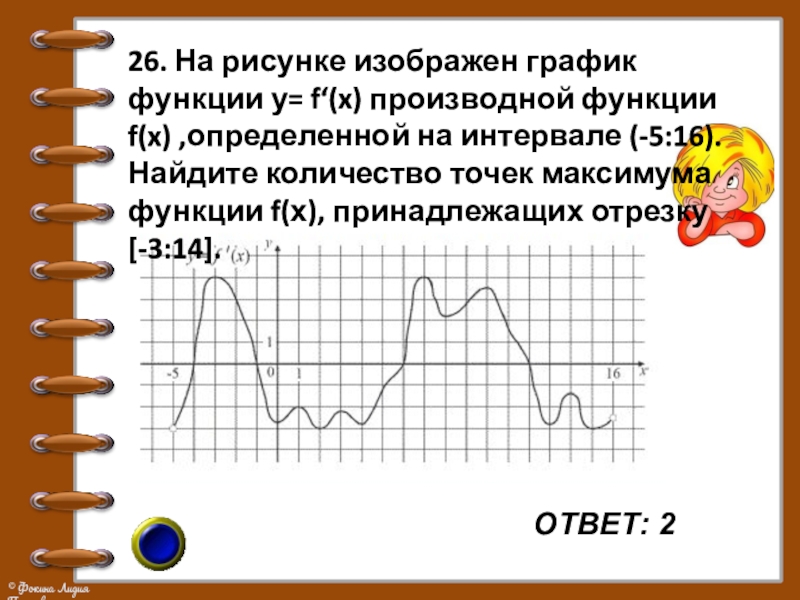
Слайд 3226. На рисунке изображен график функции у= f‘(x) производной функции f(x)
,определенной на интервале (-5:16). Найдите количество точек максимума функции f(х), принадлежащих отрезку [-3:14].
ОТВЕТ: 2
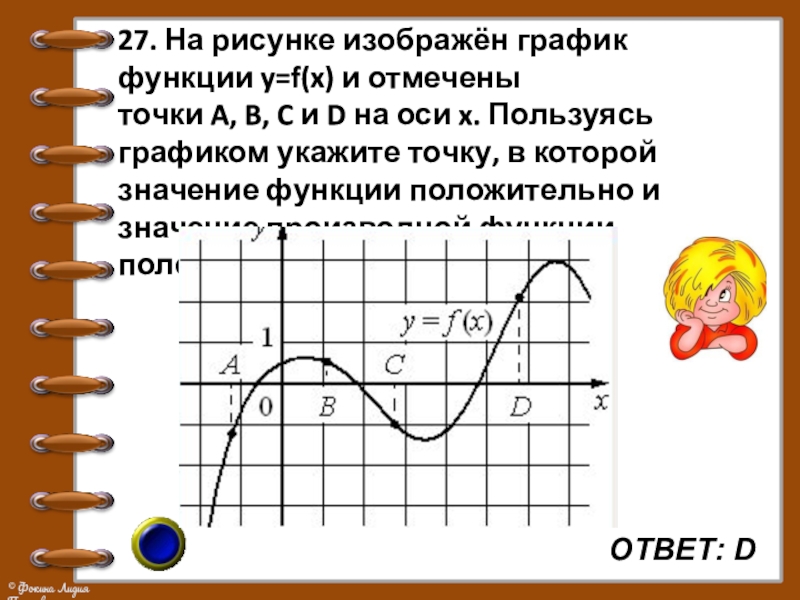
Слайд 33ОТВЕТ: D
27. На рисунке изображён график функции y=f(x) и отмечены точки A, B, C и D на оси x.
Пользуясь графиком укажите точку, в которой значение функции положительно и значение производной функции положительно.
Слайд 34ОТВЕТ: -3
28. На рисунке изображен график у=f/ (х)- производной функции
f(x). Найдите абсциссу точки, в которой касательная к графику у=f(х) параллельна оси абсцисс или совпадает с ней.
Слайд 35ОТВЕТ: 1
29. На рисунке изображен график производной функции y=g(x). Найдите количество
точек минимума.
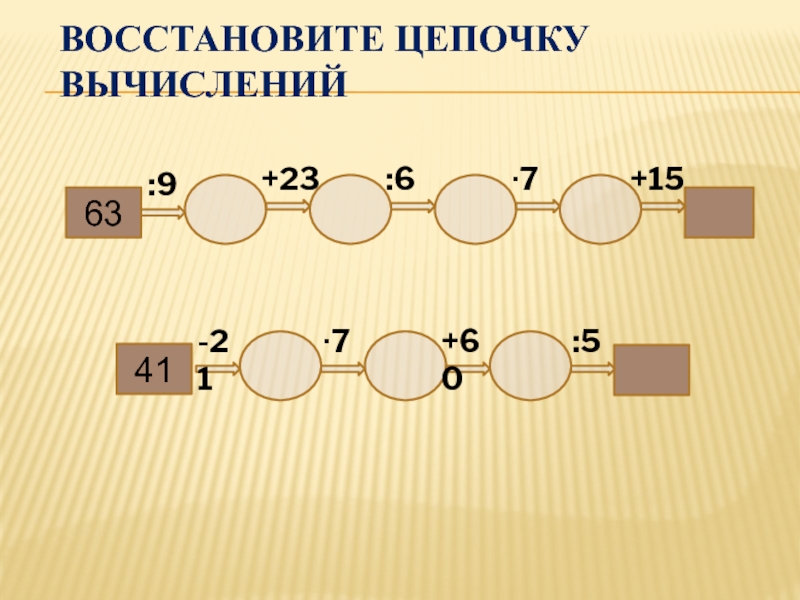
Слайд 3631. Найдите промежутки, на которых производная функции положительна.
ОТВЕТ: [-4;-3] и
[-2;0]
![31. Найдите промежутки, на которых производная функции положительна. ОТВЕТ: [-4;-3] и [-2;0]](/img/tmb/8/714455/63dcea58fd085839ebd8fa294d30f650-800x.jpg "Презентация по алгебре на тему Математическая игра по теме Производная 31. Найдите промежутки, на которых производная функции положительна. ОТВЕТ: [-4;-3] и [-2;0]")
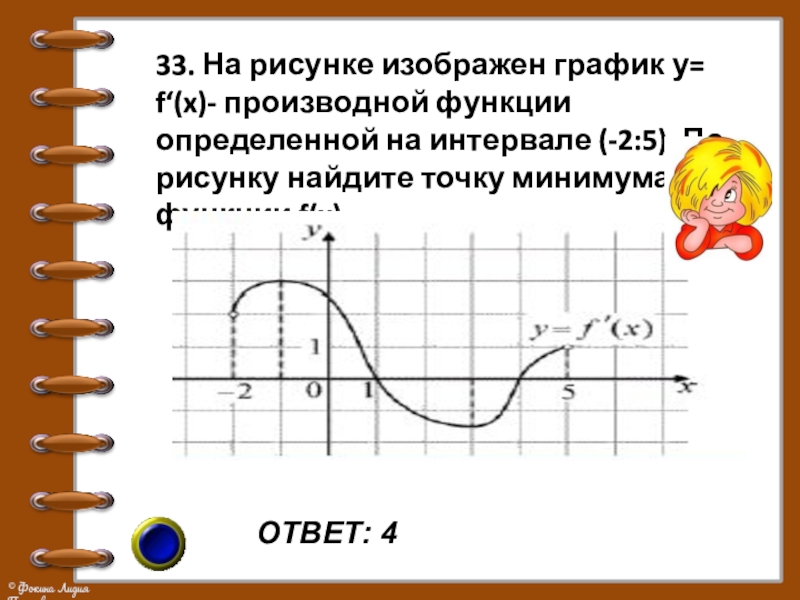
Слайд 38ОТВЕТ: 4
33. На рисунке изображен график у= f‘(x)- производной функции
определенной на интервале (-2:5). По рисунку найдите точку минимума функции f(x)
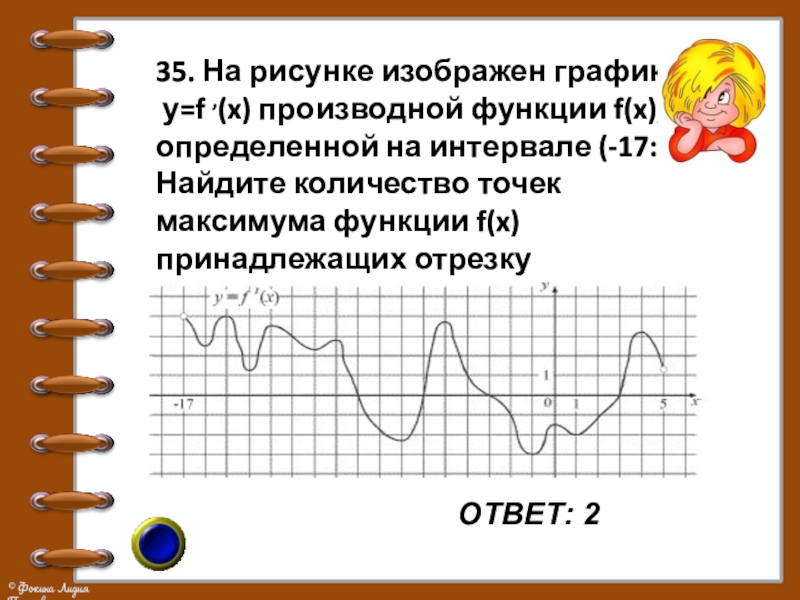
Слайд 39ОТВЕТ: 2
35. На рисунке изображен график
у=f ,(x) производной функции
f(x),
определенной на интервале (-17:5). Найдите количество точек максимума функции f(x) принадлежащих отрезку
[-10: 2].
определенной на интервале (-17:5). Найдите количество точек максимума функции f(x) принадлежащих отрезку
[-10: 2].
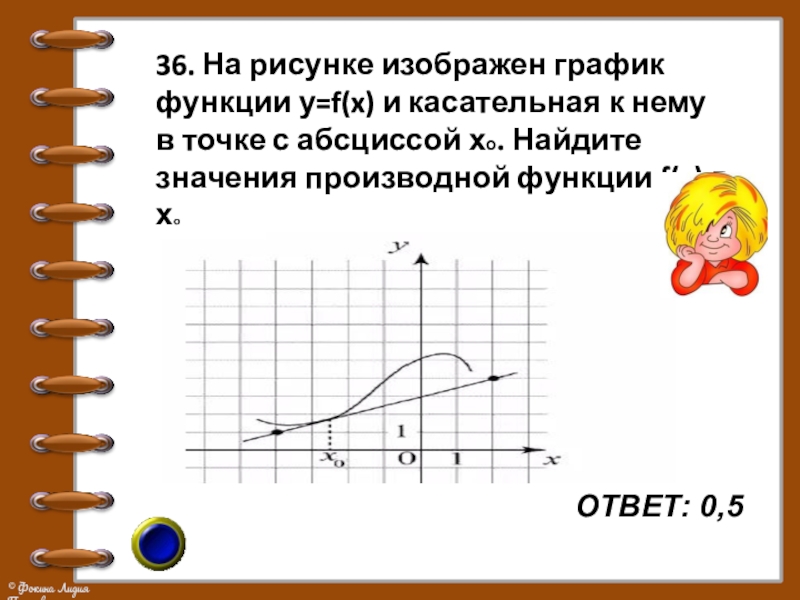
Слайд 4036. На рисунке изображен график функции у=f(x) и касательная к нему
в точке с абсциссой хо. Найдите значения производной функции f(x) в хо
ОТВЕТ: 0,5
