- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему логарифмы
Содержание
- 1. Презентация по алгебре на тему логарифмы
- 2. История логарифмов как алгебраического понятия прослеживается с
- 3. Решающий шаг был сделан в средневековой Европе.
- 4. В 1614 году шотландский математик-любитель Джон Непер
- 5. Основное свойство логарифма Непера: если величины образуют
- 6. Как вскоре обнаружилось, из-за ошибки в алгоритме
- 7. В 1620-е годы Эдмунд Уингейт и Уильям
- 8. Первые таблицы логарифмов опубликовал Джон Непер (1614),
- 9. Как пользоваться логарифмической линейкой
- 10. Она имеет как минимум три различных шкалы,
- 11. Запишите числа, которые подлежат умножению. В примере мы подсчитаем, сколько будет 260 x 0,3.
- 12. Обратите внимание на промежутки между цифрами. В отличие
- 13. Метки на шкале. Каждая шкала логарифмической линейки имеет
- 14. Понимание делений шкалы. Посмотрите на вертикальные линии на
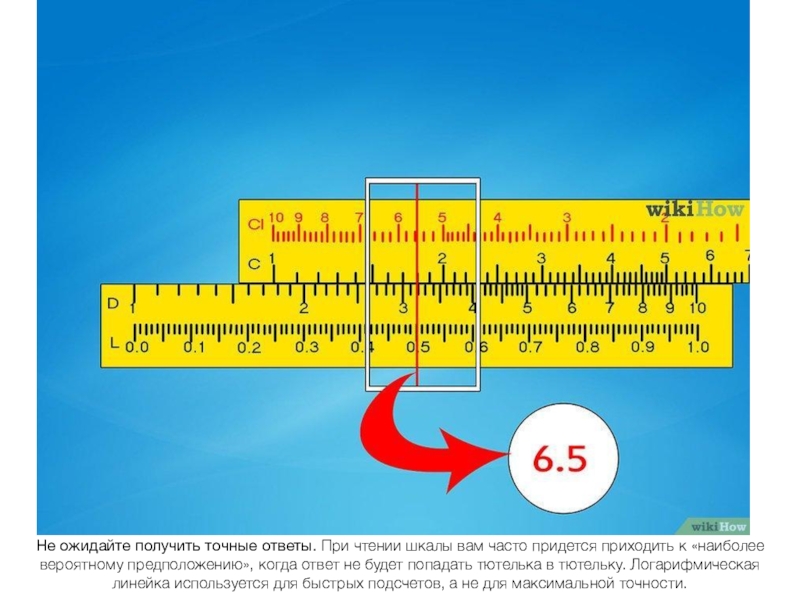
- 15. Не ожидайте получить точные ответы. При чтении
- 16. Логарифмическая линейка имеет цифры от 1 до
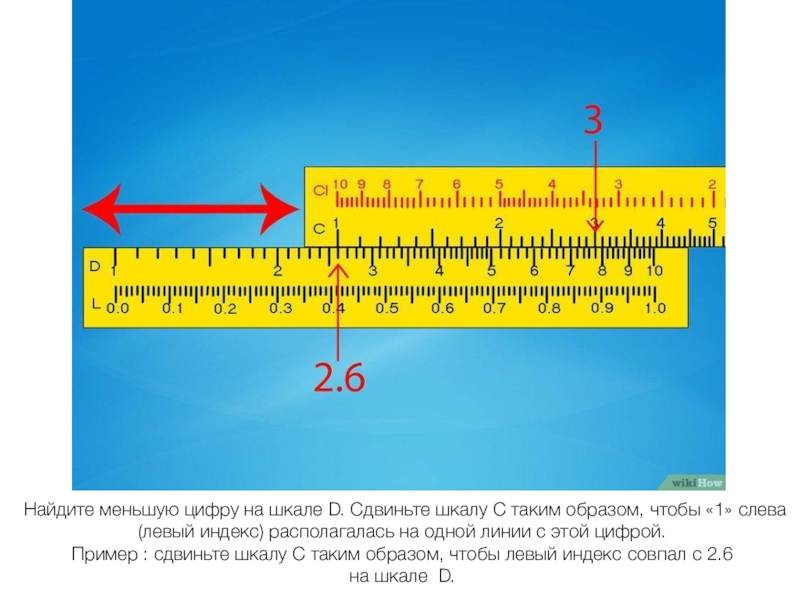
- 17. Найдите меньшую цифру на шкале D. Сдвиньте
- 18. Переместите металлический указатель ко второй цифре на
- 19. Прикидывайте правильную десятичную точку. Независимо от производимого умножения,
- 20. Слайд 20
- 21. Икосаэдр - правильный многогранник (платоново тело). Имеет двадцать граней, 12 вершин,
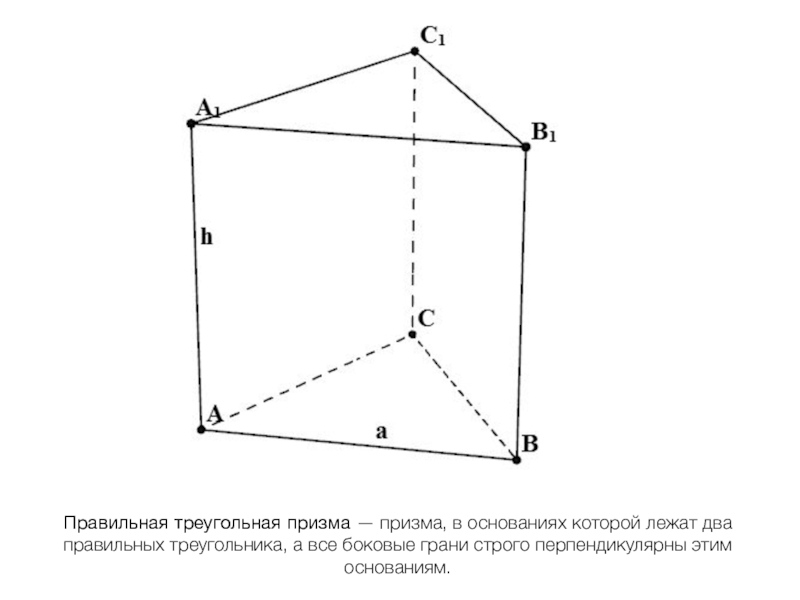
- 22. Правильная треугольная призма — призма, в основаниях которой
- 23. Большой додекаэдр - правильный звездчатый многогранник (тело Кеплера-Пуансо). Состоит из двенадцати
- 24. Малый звездчатый додекаэдр - правильный звездчатый многогранник (тело Кеплера-Пуансо). Состоит из
- 25. Слайд 25
История логарифмов как алгебраического понятия прослеживается с античных времён. Индийский математик VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4.
Слайд 2История логарифмов как алгебраического понятия прослеживается с античных времён. Индийский математик
VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4.
Слайд 3Решающий шаг был сделан в средневековой Европе. Потребность в сложных расчётах
в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел, а также извлечением корней. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, упростятся также возведение в степень и извлечение корня.
Слайд 4В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке
сочинение под названием «Описание удивительной таблицы логарифмов» (лат. Mirifici Logarithmorum Canonis Descriptio). В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'.
Джон Непер и его «удивительная таблица логарифмов»
Слайд 5Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их
логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма, например:
Слайд 6Как вскоре обнаружилось, из-за ошибки в алгоритме все значения таблицы Непера
содержали неверные цифры после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики.
Слайд 7В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую
линейку, до появления карманных калькуляторов служившую незаменимым расчётным орудием инженера. С помощью этого компактного инструмента можно быстро производить все алгебраические операции, в том числе с участием тригонометрических функций. Точность расчётов — около 3 значащих цифр.
Слайд 8Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только
логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Йост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера, Carl Bremiker).
Слайд 10Она имеет как минимум три различных шкалы, почти на каждой из
которых цифры расположены даже не на одинаковом расстоянии друг от друга. Правильно расположив нужные цифры на шкале, вы сможете выполнить умножение двух любых чисел гораздо быстрее, чем выполняя расчеты на бумаге.
Слайд 11Запишите числа, которые подлежат умножению. В примере мы подсчитаем, сколько будет
260 x 0,3.
Слайд 12Обратите внимание на промежутки между цифрами. В отличие от обычной линейки, расстояние
между ними не одинаковое. Наоборот, оно определяется по особой «логарифмической» формуле, меньше с одной стороны и больше с другой. Благодаря этому вы можете совместить две шкалы нужным образом и получить ответ на задачу по умножению.
Слайд 13Метки на шкале. Каждая шкала логарифмической линейки имеет буквенное или символьное обозначение
с левой или правой стороны. Ниже описаны общепринятые обозначения на логарифмических линейках:
Шкалы C и D похожи на одноразрядную вытянутую линейку, метки на которой расположены слева направо. Такая шкала называется «одноразрядной десятичной» шкалой.
Шкалы A и B – «двухразрядные десятичные» шкалы. Каждая состоит из двух небольших вытянутых линеек, расположенных впритык.
K – это трехразрядная десятичная шкала или три вытянутые линейки, расположенные впритык. Такая шкала имеется не на всех логарифмических линейках.
Шкалы C| и D| аналогичны C и D, но читаются справа налево. Часто они имеют красную окраску. Они присутствуют не на всех логарифмических линейках.
Слайд 14Понимание делений шкалы. Посмотрите на вертикальные линии на шкале C или D
и ознакомьтесь с тем, как они читаются:
Основные цифры на шкале начинаются с 1 от левого края и продолжаются до 9, а затем завершаются еще одной 1 справа. Обычно все они нанесены на линейку.
Вторичные деления, обозначенные чуть меньшими вертикальными линиями, разделяют каждую основную цифру на 0,1. Вас не должно сбивать с толку, если они обозначены как «1, 2, 3»; все равно они соответствуют «1,1; 1,2; 1,3» и так далее.
Также могут присутствовать меньшие деления, которые обычно соответствуют шагу 0,02. Следите за ними внимательно, так как они могут исчезать в верхней части шкалы, где цифры находятся ближе друг к другу.
Слайд 15 Не ожидайте получить точные ответы. При чтении шкалы вам часто придется приходить
к «наиболее вероятному предположению», когда ответ не будет попадать тютелька в тютельку. Логарифмическая линейка используется для быстрых подсчетов, а не для максимальной точности.
Слайд 16Логарифмическая линейка имеет цифры от 1 до 10. Переместите десятичную точку
каждого умножаемого числа, чтобы они соответствовали своим значениям.
Пример : чтобы подсчитать 260 x 0.3, начинайте вместо этого с 2.6 x 3.
Слайд 17Найдите меньшую цифру на шкале D. Сдвиньте шкалу C таким образом,
чтобы «1» слева (левый индекс) располагалась на одной линии с этой цифрой.
Пример : сдвиньте шкалу C таким образом, чтобы левый индекс совпал с 2.6
на шкале D.
Слайд 18Переместите металлический указатель ко второй цифре на шкале C. Указатель –
это металлический предмет, который перемещайте по всей линейке. Совместите указатель со второй цифрой вашей задачи на шкале C. Указатель будет указывать ответ к задаче на шкале D. Если он не перемещается так далеко, переходите к следующему шагу. Пример : переместите указатель к цифре 3 на шкале C. В этом положении он также будет указывать на 7.8 на шкале D или около того. Переходите к следующему шагу .
Слайд 19Прикидывайте правильную десятичную точку. Независимо от производимого умножения, ваш ответ всегда будет
считываться по шкале D, которая содержит лишь цифры от одного до десяти. Вам не обойтись без предположения и умственного подсчета, чтобы определить местонахождение десятичной точки в фактическом ответе. Пример : Нашей первоначальной задачей было 260 x 0.3, а линейка дала ответ 7.8. Округлите первоначальную задачу до удобных чисел и решите ее в голове: 250 x 0.5 = 125. Такой ответ гораздо ближе к 78, чем к 780 или 7.8, поэтому правильный ответ будет 78.
Слайд 21Икосаэдр - правильный многогранник (платоново тело). Имеет двадцать граней, 12 вершин, 30 ребер. Грань икосаэдра - правильный
треугольник. Каждая вершина икосаэдра является вершиной пяти правильных треугольников. Икосаэдр имеет центр симметрии и 15 осей симметрии. Каждая из осей проходит через середины противолежащих параллельных ребер. Икосаэдр имеет 15 плоскостей симметрии. Плоскости симметрии проходят через четыре вершины, которые лежат в одной плоскости, и середины противоположных параллельных ребер. Сумма плоских углов при каждой вершине равна 300º.
Слайд 22Правильная треугольная призма — призма, в основаниях которой лежат два правильных треугольника,
а все боковые грани строго перпендикулярны этим основаниям.
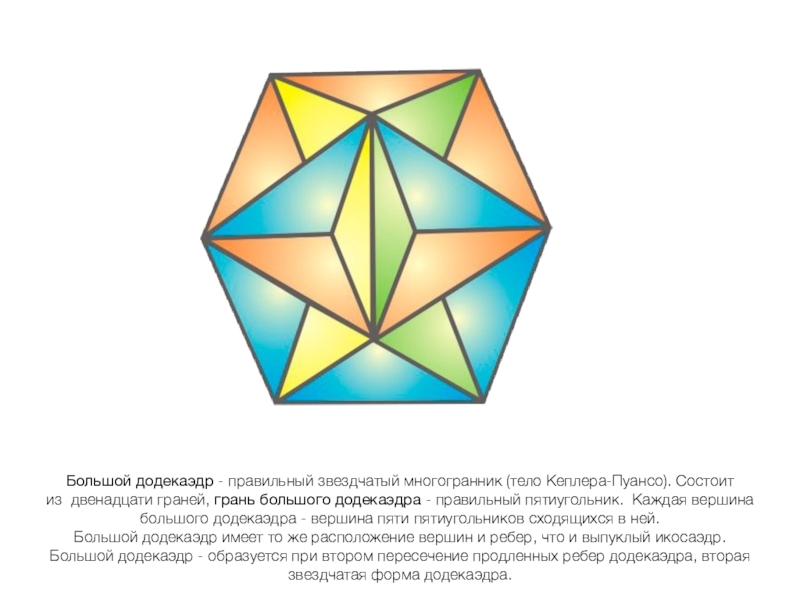
Слайд 23Большой додекаэдр - правильный звездчатый многогранник (тело Кеплера-Пуансо). Состоит из двенадцати граней, грань большого додекаэдра - правильный
пятиугольник. Каждая вершина большого додекаэдра - вершина пяти пятиугольников сходящихся в ней.
Большой додекаэдр имеет то же расположение вершин и ребер, что и выпуклый икосаэдр.
Большой додекаэдр - образуется при втором пересечение продленных ребер додекаэдра, вторая звездчатая форма додекаэдра.
Большой додекаэдр имеет то же расположение вершин и ребер, что и выпуклый икосаэдр.
Большой додекаэдр - образуется при втором пересечение продленных ребер додекаэдра, вторая звездчатая форма додекаэдра.
Слайд 24Малый звездчатый додекаэдр - правильный звездчатый многогранник (тело Кеплера-Пуансо). Состоит из двенадцати граней, грань малого звездчатого
додекаэдра - правильная пятиконечная звезда, пентаграмма. Каждая вершина малого звездчатого додекаэдра - вершина пяти пентаграмм сходящихся в ней.
Малый звездчатый додекаэдр можно получить продолжив грани правильного выпуклого додекаэдра до их первого пересечения. Это обстоятельство позволяет считать малый звездчатый додекаэдр, первой звездчатой формой додекаэдра. Название многограннику дал Артур Кэли. Малый звездчатый додекаэдр имеет то же расположение вершин, что и выпуклый правильный икосаэдр и расположение рёбер, как у большого икосаэдра.
Малый звездчатый додекаэдр можно получить продолжив грани правильного выпуклого додекаэдра до их первого пересечения. Это обстоятельство позволяет считать малый звездчатый додекаэдр, первой звездчатой формой додекаэдра. Название многограннику дал Артур Кэли. Малый звездчатый додекаэдр имеет то же расположение вершин, что и выпуклый правильный икосаэдр и расположение рёбер, как у большого икосаэдра.