- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Логарифмы (10 класс)
Содержание
- 1. Презентация по алгебре на тему Логарифмы (10 класс)
- 2. Слайд 2
- 3. ЗадачиПознакомиться с историей происхождения логарифмов
- 4. Из истории логарифмовВ течении XVI в.резко возрос
- 5. В 1614 году шотландский математик Джон Непер(1550
- 6. Практическое применение логарифмы находят в …Криптографии, где
- 7. ОпределениеЛогарифмом положительного числа x по положительному и
- 8. обозначения:Натуральный логарифм – это логарифм числа по
- 9. Знаете ли вы…Способ для запоминания простой –
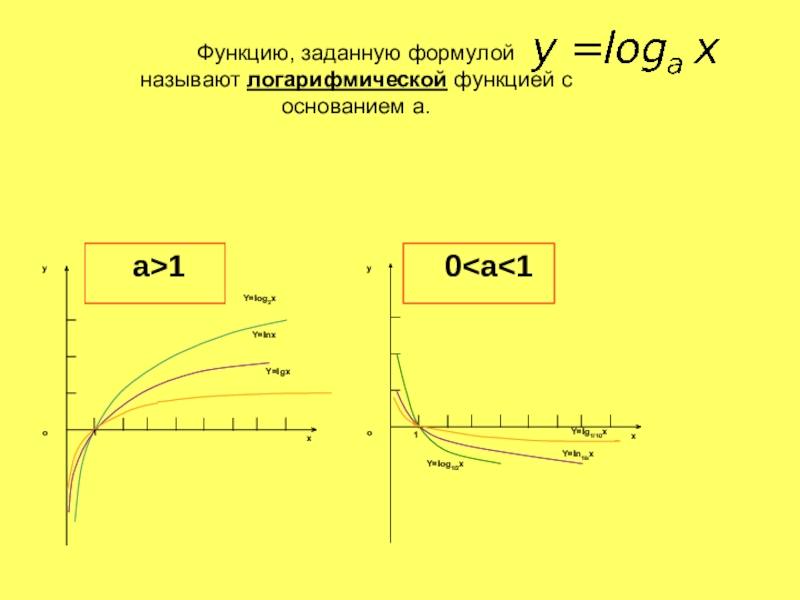
- 10. Функцию, заданную формулой называют логарифмической функцией с основанием а.a>10
- 11. СВОЙСТВА ФУНКЦИИПри а>1 D(f)=(0;∞) – область
- 12. Свойства логарифмов при любом a>0 ( a≠1
- 13. ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯПример 1 (А).Упростите выражение
- 14. УРАВНЕНИЯПРИМЕР3(А)УКАЖИТЕ ПРОМЕЖУТОК, КОТОРОМУ ПРИНАДЛЕЖИТ КОРЕНЬ УРАВНЕНИЯ
- 15. Пример4(с).Найдите все значения a , при каждом
- 16. Пример 5(с).При каких значениях параметра a уравнениеимеет
- 17. неравенстваПример6(A). решите неравенство:1) (-∞; 4.5) 2)
- 18. Пример 9(B) Решите неравенство log2x – 5(5x
- 19. функциипример9(A).найдите область определения функции 1) (0;+∞)
- 20. ПРИМЕР11 (А). Укажите область определения функции. 1)
- 21. 1.Найдите значение выражения2. Найдите область определения функции4.
- 22. Карточка 1Сформулируйте определение логарифмической функции, определение логарифма
Слайд 2
НЕТ НИ ОДНОЙ ОБЛАСТИ МАТЕМАТИКИ , КАК БЫ АБСТРАКТНА
ОНА НИ БЫЛА , КОТОРАЯ КОГДА – НИБУДЬ НЕ ОКАЖЕТСЯ
ПРИМЕНИМОЙ К ЯВЛЕНИЯМ ДЕЙСТВИТЕЛЬНОГО МИРА.
Н.И. ЛОБАЧЕВСКИЙ.
Слайд 3Задачи
Познакомиться с историей происхождения логарифмов и их практическим применением
Повторить
Отработать навыки решения задач, предлагаемых на ЕГЭ
Закрепить знания, умения и навыки
Слайд 4Из истории логарифмов
В течении XVI в.резко возрос объем работы, связанный с
Слайд 5В 1614 году шотландский математик Джон Непер(1550 - 1617) изобрел таблицы
Швейцарский часовщик и мастер астрономических приборов, любитель математики. И. Бюрги (1552 - 1632)составил первые таблицы логарифмов. Долгое время он не решался публиковать таблицы, медлительность Бюрги стоила ему приоритета. Только в 1620 году издал свою книгу "Таблицы арифметической и геометрической прогрессии с обстоятельным наставлением, как пользоваться ими при всякого рода вычислениях".
Слайд 6Практическое применение логарифмы находят в …
Криптографии, где логарифмы по основанию 2
При измерения параметров различной радиоаппаратуры ( систем телефонии ,в системах передачи информации (модемы) ) была введена единица под названием "Бел" - в честь американского ученого A.G. Bell, (1847-1922гг). Бел [Б] - единица логарифмической величины, служащая для измерения разности уровней одноименных энергетических (мощность, энергия и т.п.) или силовых (напряжение, сила тока и т.п.) величин. Из-за крупности единица "Бел" не нашла широкого применения, а вот её десятая доля (0.1 Б) прочно заняла своё место в практике измерений. Как известно, для десятой доли используется приставка Деци-, поэтому дольную единицу звали ДЕЦИБЕЛ [дБ ] [dB].
В акустике для измерения громкости звука.
Слайд 7Определение
Логарифмом положительного числа x по положительному и отличному от единицы основанию
Слайд 8обозначения:
Натуральный логарифм – это логарифм числа по основанию е
Десятичный логарифм –
Слайд 9Знаете ли вы…
Способ для запоминания простой – два, семь ,дважды ЛевТолстой
e ≈ 2,718281828...
Это я знаю и помню прекрасно
π ≈ 3 , 1 4 1 5 9….
π ≈ 3,14159…
Два замечательных рациональных приближения числа ∏
π ≈ - древнейшее, открыто знаменитым китайским
астрономом Цю-Шунь-Ши в 5 веке до н. э.
π ≈ -открыто Архимедом.
Слайд 11СВОЙСТВА ФУНКЦИИ
При а>1
D(f)=(0;∞) – область определения
E(f)=R
Функция возрастает на D(f);
y=0 при x=1;
у>0 при x>1; у<0 при 0
При 0<а<1
D(f)=(0;∞) – область определения
E(f)=R – множество значений
Функция убывает на D(f);
y=0 при x=1;
у>0 при 0
Функции y=logax и y=ax взаимно обратны, их графики симметричны относительно прямой y=x.
Слайд 12Свойства логарифмов
при любом a>0 ( a≠1 ) и любых х>0,
Логарифм частного
Логарифм степени
Логарифм произведения
Основное логарифмическое тождество
Формула перехода
Слайд 13ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ
Пример 1 (А).Упростите выражение lg25+0.5lg16.
Решение. Применив свойство логарифма степени ко второму слагаемому, а затем свойство суммы логарифмов, получим:
Lg25+0.5lg16=lg25+lg161/2=lg25+lg4=lg(25*4)=lg100=2.Ответ: 2.
Пример 2 (В). Найдите значение выражения
Решение. Значение первого слагаемого можно найти с помощью основного логарифмического тождества:
Применяя ко второму и третьему слагаемому формулы
Получаем :
Значит, Ответ: 2
Слайд 14УРАВНЕНИЯ
ПРИМЕР3(А)УКАЖИТЕ ПРОМЕЖУТОК, КОТОРОМУ ПРИНАДЛЕЖИТ КОРЕНЬ УРАВНЕНИЯ
Решение. Данное уравнение равносильно системе
Которая равносильна системе
Решая уравнение ,получаем: x=2 или x=-4
Число -4 не удовлетворяет условию x>0, т.е. является посторонним корнем.
Число 2 удовлетворяет условию x>0, значит, является корнем исходного
уравнения. Этот корень принадлежит промежутку, указанному в третьем варианте ответа.
ответ: 3
Слайд 15Пример4(с).Найдите все значения a , при каждом из которых уравнение
Имеет два
Введем обозначение .уравнение примет вид:
Его корни - числа . следовательно, ;
Отсюда получаем:
Точка x=42 равноудалена от точек ,т.е. она является серединой отрезка с концами в этих точках.
Воспользуемся формулой координаты середины отрезка
Далее получаем:
ответ: при a=1.
Ответ:a=1
Слайд 16Пример 5(с).
При каких значениях параметра a уравнение
имеет ровно четыре корня?
Решение.
О.Д.З. : x > 0.
Пусть Тогда уравнение должно иметь два
положительных корня, то есть при D>0 и .
Таким образом,
откуда
Ответ: при
Слайд 17неравенства
Пример6(A).
решите неравенство:
1) (-∞; 4.5) 2) (0;+∞) 3) (2.5;
Решение. Представим правую часть неравенства в
виде логарифма с основанием ½.
Получим неравенство
Так как функция определена и
убывает на промежутке (0;+∞), то данное
Неравенство равносильно следующей системе
2x-5>4,
2x-5>0.
Данная система равносильна неравенству 2x-5>4, или x>4.5.
Значит, решением данного неравенства является промежуток (4.5;+∞).
ответ: 4.
Пример 7(А).
Решите неравенство:
1) (1;+∞) 2) (0;+∞) 3) (-∞;-4) 4) (-4;+∞)
Так как функция определена и
возрастает на промежутке (0;+∞) , то данное неравенство равносильно следующей системе
2x+3>x-1,
x-1>0,
2X+3>0.
Решая неравенства системы, получаем
x>-4,
x>1.
Значит, решением данного неравенства является промежуток (1;+∞).
ответ: 1
Слайд 18Пример 9(B) Решите неравенство log2x – 5(5x – 2) і1.
Решение. Неравенство
Пример 9(B) Решите неравенство
Решение. Неравенство равносильно совокупности двух систем неравенств:
Решаем первую из этих систем:
Решаем вторую систему:
Решением исходного неравенства является объединение двух решений этих систем, т.е. Ответ:
Слайд 19
функции
пример9(A).найдите область определения функции
1) (0;+∞) 2)(0;0.09]
Решение. Функция
определена на промежутке [0;+∞), поэтому
≥0,
Т.е. ≤2
Представим правую часть полученного неравенства в виде логарифма с основанием 0.3:
≤
Поскольку функция определена и убывает на
промежутке (0;+∞) то данное неравенство равносильно неравенству x≥0.09.
Значит, решением данного неравенства является промежуток [0.09;+∞).
Ответ:3
Пример10(В).найдите наименьшее значение функции
Решение. функция монотонно убывает на всей области определения. Поскольку область определения логарифмической функции- множество всех положительных чисел, то >0,
отсюда следует, что (x-0.5)(x+0.5)<0,
-0.5
График квадратичной функции -парабола, вершина которой находится на оси ординат в точке (0;0.25), а ветви направлены вниз.
Поэтому свое наибольшее значение 0.25 эта функция достигает при x=0.
При 0≤х≤0.5 значения функции
Непрерывно убывают от 0.25 до 0, а при -0.5≤х≤0- непрерывно возрастают от 0 до 0.25.
Следовательно, на промежутке -0.5<х≤0 функция
непрерывно убывает, принимая наименьшее значение у(0)=2, а на промежутке 0≤х<0.5 непрерывно возрастает, принимая наименьшее значение у(0)=2.
ответ: 2
Слайд 20
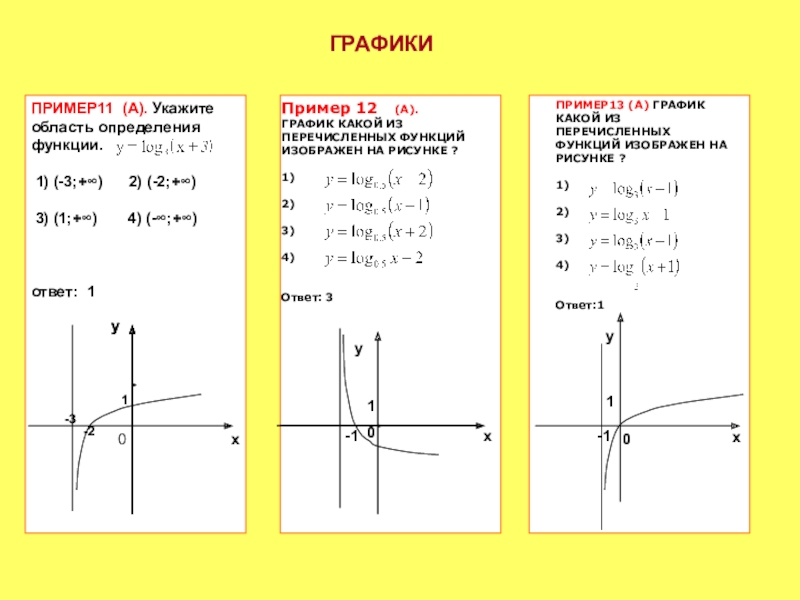
ПРИМЕР11 (А). Укажите область определения функции.
1) (-3;+∞) 2)
3) (1;+∞) 4) (-∞;+∞)
ответ: 1
Пример 12 (А).
ГРАФИК КАКОЙ ИЗ ПЕРЕЧИСЛЕННЫХ ФУНКЦИЙ ИЗОБРАЖЕН НА РИСУНКЕ ?
1)
2)
3)
4)
Ответ: 3
ПРИМЕР13 (А) ГРАФИК КАКОЙ ИЗ ПЕРЕЧИСЛЕННЫХ ФУНКЦИЙ ИЗОБРАЖЕН НА РИСУНКЕ ?
1)
2)
3)
4)
Ответ:1
ГРАФИКИ
Слайд 211.Найдите значение выражения
2. Найдите область определения функции
4. Укажите промежуток , которому
5. решите неравенство <
y
Проверь себя!
3. График какой из перечисленных функций изображен на рисунке?
Слайд 22Карточка 1
Сформулируйте определение логарифмической функции, определение логарифма числа. Запишите основное логарифмическое
Найдите область определения функции
Упростите выражение
Решите систему уравненеий
Решите неравенство












![Презентация по алгебре на тему Логарифмы (10 класс) УРАВНЕНИЯПРИМЕР3(А)УКАЖИТЕ ПРОМЕЖУТОК, КОТОРОМУ ПРИНАДЛЕЖИТ КОРЕНЬ УРАВНЕНИЯ 1) (-∞:-2] УРАВНЕНИЯПРИМЕР3(А)УКАЖИТЕ ПРОМЕЖУТОК, КОТОРОМУ ПРИНАДЛЕЖИТ КОРЕНЬ УРАВНЕНИЯ 1) (-∞:-2]](/img/thumbs/d0071af6692e1f74614eb3bb6d8fc364-800x.jpg)




![Презентация по алгебре на тему Логарифмы (10 класс) функциипример9(A).найдите область определения функции 1) (0;+∞) 2)(0;0.09] 3)[0.09;+∞) 4) функциипример9(A).найдите область определения функции 1) (0;+∞) 2)(0;0.09] 3)[0.09;+∞) 4) [0;+∞)Решение. Функция](/img/thumbs/f8ca71650fe073e5bdced66cbe9d20e4-800x.jpg)