- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Линейные и квадратные неравенства (1-2 урок)
Содержание
- 1. Презентация по алгебре на тему Линейные и квадратные неравенства (1-2 урок)
- 2. Процент – сотая часть целого1% = 0,0110%
- 3. Записать проценты в виде десятичной дроби10% 32%12%4%200%110%50%1,5%
- 4. Записать десятичную дробь в виде процентов:0,2 0,030,484,50,67110,50,06
- 5. Решить задачу:Автомобиль проехал 15% от всего пути.
- 6. Линейные и квадратные неравенства
- 7. Линейные и квадратные неравенстваЛН с одной переменной х называют неравенство вида:ax+b>0, ax+b0, ax2+bx+c
- 8. Решение неравенствЗначение переменной х, которое обращает неравенство
- 9. Равносильные преобразования неравенствПравило 1:Любой компонент неравенства можно
- 10. Равносильные преобразования неравенствПравило 2:Обе части неравенства можно
- 11. Равносильные преобразования неравенствПравило 3:Обе части неравенства можно
- 12. Равносильные преобразования неравенствПравило 2*:Обе части неравенства можно
- 13. Равносильные преобразования неравенствПравило 3*:Обе части неравенства можно
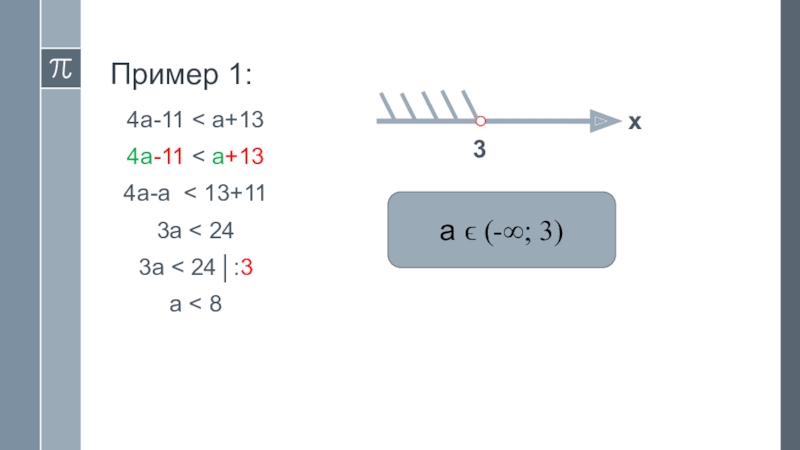
- 14. Пример 1: 4a-11 < a+134a-11 < a+134a-a
- 15. Пример 2:3x+9 < 2x2-2x2 +3x+9 < 0
- 16. Особые случаи решений квадратных уравненийЕсли квадратный трехчлен
- 17. Особые случаи решений квадратных уравненийЕсли квадратный трехчлен не имеет корней (D
- 18. Теорема 2x2 - x+4>0D= -31 0При любом
- 19. Теорема -x2 +3x-8>0D= -23 0 имеет отрицательный
- 20. Повторим:Какой вид имеет линейное неравенство?Какой вид имеет
- 21. Домашнее заданиеП. 1 ( стр. 5-11)№ 1.2
Слайд 2Процент – сотая часть целого
1% = 0,01
10% = 0,1
100% = 1
Найти
Найти целое по проценту:
Разделить целое на сто и умножить на число процентов:
20% от 80
800:100*20=16
Разделить часть от целого на число процентов и умножить на 100:
20% это 40
40:20*100=200
Слайд 5Решить задачу:
Автомобиль проехал 15% от всего пути. Сколько проехал автомобиль, если
200:100=2(км) – 1%
2*15=30 (км) – 15%
Отремонтировано 70% всего дорожного покрытия, что составило 140 км. Какова протяженность всей дороги?
140:70=2(км) – 1%
2*100=200(км) – 100%
Слайд 7Линейные и квадратные неравенства
ЛН с одной переменной х называют неравенство вида:
ax+b>0,
ЛН с одной переменной х называют неравенство вида:
ax2+bx+c>0, ax2+bx+c<0 (a, b, c – действительные числа, но a≠0)
Работа в парах: запишите несколько примеров неравенств и проверьте друг друга
Слайд 8Решение неравенств
Значение переменной х, которое обращает неравенство f(x)>0 в верное числовое
Пример: x>0, если х=5, то неравенство будет иметь вид 5>0 (х=5 – частное решение).
Множество всех частных решений – общее решение.
Пример: x>0, решением будут все отрицательные числа хϵ(-∞; 0).
Слайд 9Равносильные преобразования неравенств
Правило 1:
Любой компонент неравенства можно перенести из одной части
2х+1 > 0
2х > -1
Слайд 10Равносильные преобразования неравенств
Правило 2:
Обе части неравенства можно умножить или разделить на
2х+1 > 0 │*2
2*2х+2*1 > 2*0
4х+2>0
Слайд 11Равносильные преобразования неравенств
Правило 3:
Обе части неравенства можно умножить или разделить на
2х+1 > 0 │*(-2)
(-2)*2х+(-2)*1 > (-2)*0
-4х-2<0
Слайд 12Равносильные преобразования неравенств
Правило 2*:
Обе части неравенства можно умножить или разделить на
Слайд 13Равносильные преобразования неравенств
Правило 3*:
Обе части неравенства можно умножить или разделить на
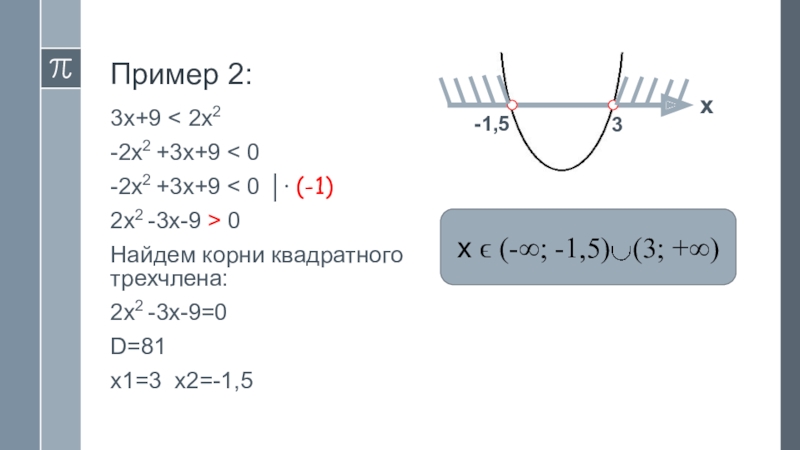
Слайд 15Пример 2:
3x+9 < 2x2
-2x2 +3x+9 < 0
-2x2 +3x+9 < 0
2x2 -3x-9 > 0
Найдем корни квадратного трехчлена:
2x2 -3x-9=0
D=81
x1=3 x2=-1,5
x ϵ (-∞; -1,5) (3; +∞)
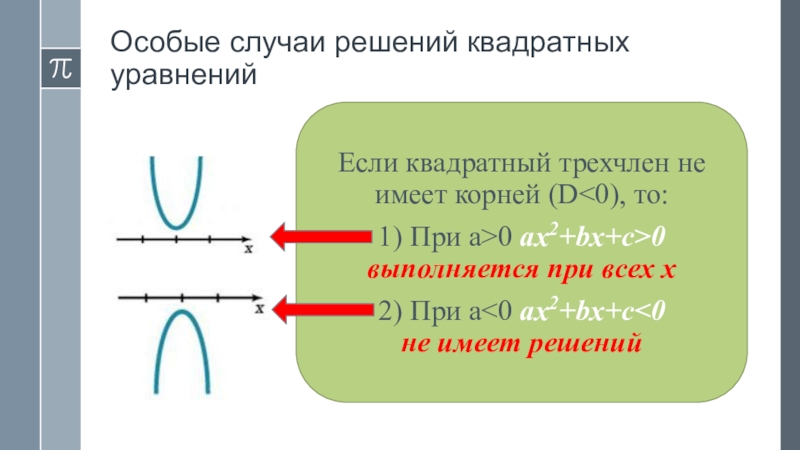
Слайд 16Особые случаи решений квадратных уравнений
Если квадратный трехчлен не имеет корней (D
1) При а>0 ax2+bx+c>0 выполняется при всех х
2) При a<0 ax2+bx+c<0 не имеет решений
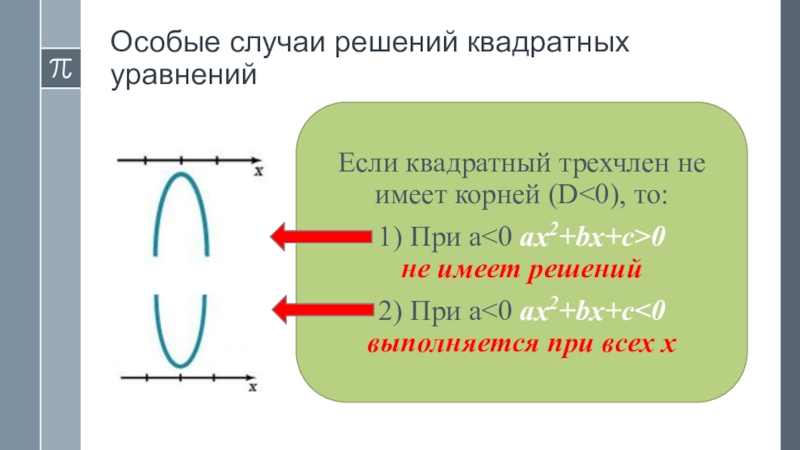
Слайд 17Особые случаи решений квадратных уравнений
Если квадратный трехчлен не имеет корней (D
1) При а<0 ax2+bx+c>0 не имеет решений
2) При a<0 ax2+bx+c<0 выполняется при всех х
Слайд 18Теорема
2x2 - x+4>0
D= -31 0
При любом значении
+ > +
Если квадратный трехчлен ax2+bx+c>0 имеет отрицательный дискриминант, то при любом х значение трехчлена имеет знак старшего коэффициента a.
Слайд 19Теорема
-x2 +3x-8>0
D= -23
- > +
Если квадратный трехчлен ax2+bx+c>0 имеет отрицательный дискриминант, то при любом х значение трехчлена имеет знак старшего коэффициента a.
Слайд 20Повторим:
Какой вид имеет линейное неравенство?
Какой вид имеет квадратное неравенство?
Что является частным
Что значит «общее решение» неравенства?
Какие равносильные преобразования неравенств вы знаете?
Как решается квадратное неравенство, если его квадратный трехчлен не имеет корней?
Слайд 21Домашнее задание
П. 1 ( стр. 5-11)
№ 1.2 (г), 1.3 (г), 1.5
*№ 1.20 (в, в), 1.21 (а, в)
* - индивидуально