Выполнил:
учитель математики Баранова Н.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Линейная функция и ее график
Содержание
- 1. Презентация по алгебре на тему Линейная функция и ее график
- 2. Цели:Повторить алгоритм построения графика линейной функции.Рассмотреть расположение
- 3. Графиком линейной функции y = kx +
- 4. Пример 1Построить график функции у = 2х
- 5. Пример 2Построить график функции а) у =
- 6. Пример 2Построить график функции а) у =
- 7. Вывод:Величина k определяет наклон графика функции y
- 8. Построить график функции а) у = -31.
- 9. Ответить на вопросы:1. Какой алгоритм построения графика
Слайд 1Линейная функция
и ее график
Алгебра
7 класс
Муниципальное бюджетное общеобразовательное учреждение
основная общеобразовательная
Слайд 2Цели:
Повторить алгоритм построения графика линейной функции.
Рассмотреть расположение графика функции у=kх+b на
Научить строить график функции y = kx + b
Научить по графику находить значение y, соответствующее x и значение x которому соответсивует значение y.
Слайд 3Графиком линейной функции y = kx + b является прямая.
Линейной функцией
где х- независимая переменная,
k и b – некоторые числа
Слайд 4Пример 1
Построить график функции
у = 2х + 3, найти точку
1. Составим таблицу значений:
2. Получим точки:
(0; 3), (1; 5)
3. Построим эти точки и
через них проведем прямую.
(0; 3)
3
(1; 5)
у = 2х + 3
Если k > 0, то угол наклона
прямой у = kx + b к оси x острый
k = 2
Точка пересечения с осью у: (0; 3) т. е. при b = 3
Слайд 5Пример 2
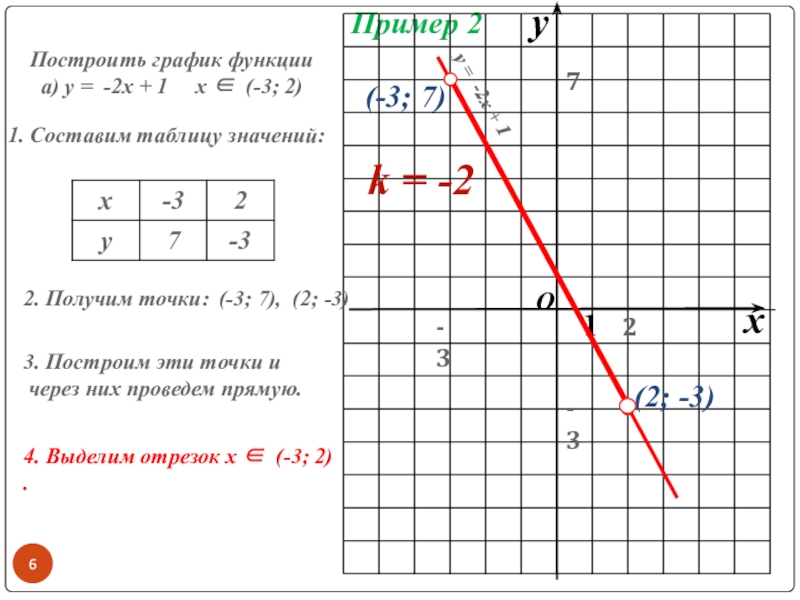
Построить график функции
а) у = -2х + 1
1. Составим таблицу значений:
2. Получим точки:
(-3; 7), (2; -3)
3. Построим эти точки и
через них проведем прямую.
(-3; 7)
(2; -3)
4. Выделим отрезок х ∈ [-3; 2] .
Если k < 0, то угол наклона
прямой у = kx + b к оси x тупой.
k = -2
у = -2х + 1
Точка пересечения с осью у: (0; 1) т. е. при b = 1
Слайд 6Пример 2
Построить график функции
а) у = -2х + 1
1. Составим таблицу значений:
2. Получим точки:
(-3; 7), (2; -3)
3. Построим эти точки и
через них проведем прямую.
(-3; 7)
(2; -3)
4. Выделим отрезок х ∈ (-3; 2) .
k = -2
у = -2х + 1
Слайд 7Вывод:
Величина k определяет наклон графика
функции y = kx + b
Если k < 0, то угол наклона
прямой у = kx + b к оси x тупой.
Если k > 0, то , то угол наклона
прямой у = kx + b к оси x острый.
Если k = 0, то линейная функция
у = kx + b параллельна оси абсцисс
(или совпадает с ней).
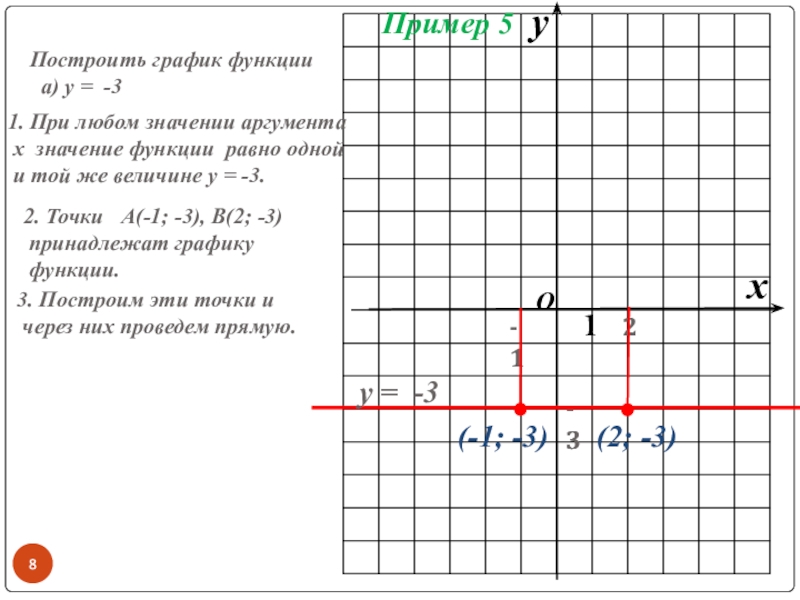
Слайд 8Построить график функции
а) у = -3
1. При любом значении аргумента
х значение функции равно одной
и той же величине у = -3.
2. Точки А(-1; -3), В(2; -3)
принадлежат графику
функции.
3. Построим эти точки и
через них проведем прямую.
(-1; -3)
(2; -3)
у = -3
Пример 5
Слайд 9Ответить на вопросы:
1. Какой алгоритм построения графика линейной
функции?
2. Какую
3. Что является графиком линейной функции? Как
можно построить такой график?
4. Как найти точку пересечения графика с осью ординат?
5. Смысл величин k и b в формуле линейной функции?
6. Какая прямая будет графиком функции при k = 0?
7. Как влияет k на угол наклона прямой?




![Презентация по алгебре на тему Линейная функция и ее график Пример 2Построить график функции а) у = -2х + 1 Пример 2Построить график функции а) у = -2х + 1 х ∈ [-3; 2]1. Составим](/img/thumbs/1c088de8a7469c6df0e9130320bd4559-800x.jpg)