- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Квадратные уравнения (8 класс)
Содержание
- 1. Презентация по алгебре на тему Квадратные уравнения (8 класс)
- 2. Определение квадратного уравненияУравнение вида ax²+bx+c=0, где x
- 3. Коэффициентыa – первый коэффициент;b – второй коэффициент;c
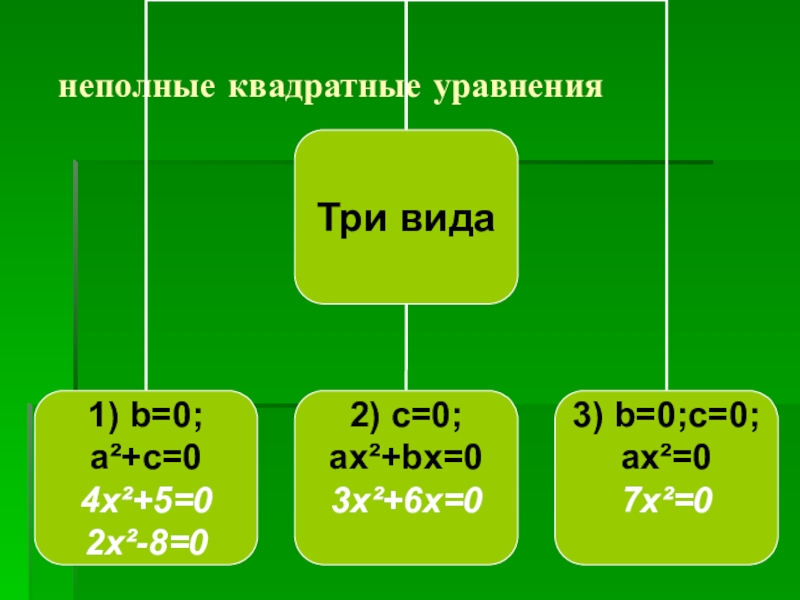
- 4. неполные квадратные уравнения
- 5. Приведенные квадратные уравненияКвадратное уравнение называется приведенным, если
- 6. Способы решения квадратных уравнений.Решение неполных:1) 4x²+5=0
- 7. Способы решения квадратных уравненийРешение приведенных: выделением квадрата
- 8. Способы решения квадратных уравненийПо формуле:D=b²-4ac,где D –
- 9. Способы решения квадратных уравненийПо теореме Виета:
Определение квадратного уравненияУравнение вида ax²+bx+c=0, где x – переменная, a, b и c - некоторые числа, причем a ≠ 0 , называется квадратным уравнением.
Слайд 2Определение квадратного уравнения
Уравнение вида ax²+bx+c=0, где x – переменная, a, b
и c - некоторые числа, причем a ≠ 0 , называется квадратным уравнением.
Слайд 3Коэффициенты
a – первый коэффициент;
b – второй коэффициент;
c - свободный член.
Пример: 2x²-3x-7=0
a=2; b=-3; c=7.
Задание. Определите коэффициенты квадратных уравнений:
-x²-4x+5=0; 8x²+4x-2=0; x²-3x=2; 6x+3x²-5=0
Задание. Определите коэффициенты квадратных уравнений:
-x²-4x+5=0; 8x²+4x-2=0; x²-3x=2; 6x+3x²-5=0
Слайд 5Приведенные квадратные уравнения
Квадратное уравнение называется приведенным, если коэффициент a=1.
x²+px+q=0
Например: x²-8x-9=0
x²+12x+36=0.
Например: x²-8x-9=0
x²+12x+36=0.
Слайд 6Способы решения квадратных уравнений.
Решение неполных:
1) 4x²+5=0 2) 2х²-8=0
3) 3х²+6x=0
4x²=-5 2х²=8 x(3x+2)=0
x²=-1,25 x²=4 x=0 или3х+2=0
Корней нет x=±2 х=-⅔
4) 7x²=0
х=0
4x²=-5 2х²=8 x(3x+2)=0
x²=-1,25 x²=4 x=0 или3х+2=0
Корней нет x=±2 х=-⅔
4) 7x²=0
х=0
Слайд 7Способы решения квадратных уравнений
Решение приведенных: выделением квадрата двучлена
x²+12x+36=0
x²-8x-9=0
(x+6)²=0 x²-8x+16-16-9=0
x+6=0 (x-4)²=25
x=-6 x-4=5 или x-4=-5
x=9 или x=-1
(x+6)²=0 x²-8x+16-16-9=0
x+6=0 (x-4)²=25
x=-6 x-4=5 или x-4=-5
x=9 или x=-1
Слайд 8Способы решения квадратных уравнений
По формуле:
D=b²-4ac,где D – дискриминант
Если D>0, то будет
2 корня
x=(-b±√D) ∕2a
Если D=0, то будет 1 корень
x=-b∕2a
3. Если D<0, то нет корней.
x=(-b±√D) ∕2a
Если D=0, то будет 1 корень
x=-b∕2a
3. Если D<0, то нет корней.
Слайд 9Способы решения квадратных уравнений
По теореме Виета:
x²+px+q=0
сумма корней равна –p,
а произведение корней равно q.
а произведение корней равно q.