- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему: Квадратичная функция (9класс)
Содержание
- 1. Презентация по алгебре на тему: Квадратичная функция (9класс)
- 2. ОГЛАВЛЕНИЕ:Титульный лист ОглавлениеВведение Историческая справкаКвадратичная функция Квадратный трехчленЗаключение Библиографический список
- 3. Введение Знаете ли вы, что
- 4. …Первобытная мама по имени…впрочем, у неё, наверное,
- 5. Пусть х - количество яблок,
- 6. Получается, что мама решила задачу
- 7. Задачи: изучив литературу по данной теме, исследовать
- 8. Гипотеза: если исследовать свойства квадратичной функции, ее
- 9. Историческая справка
- 10. ПроизводствоВернёмся и мы к квадратным уравнениям. Вспомним
- 11. А если раскрыть скобки, то из уравнения
- 12. Случай же 3 есть просто другая форма
- 13. В простейших случаях можно и не выполнять
- 14. Обратимся теперь к четвертому киту школьной алгебры
- 15. Знаменитый древнегреческий ученый Г е р о
- 16. Очень важный шаг был сделан в Древнем
- 17. Позднее, в связи с развитием астрономии
- 18. Исследуем квадратичную функцию
- 19. График функции
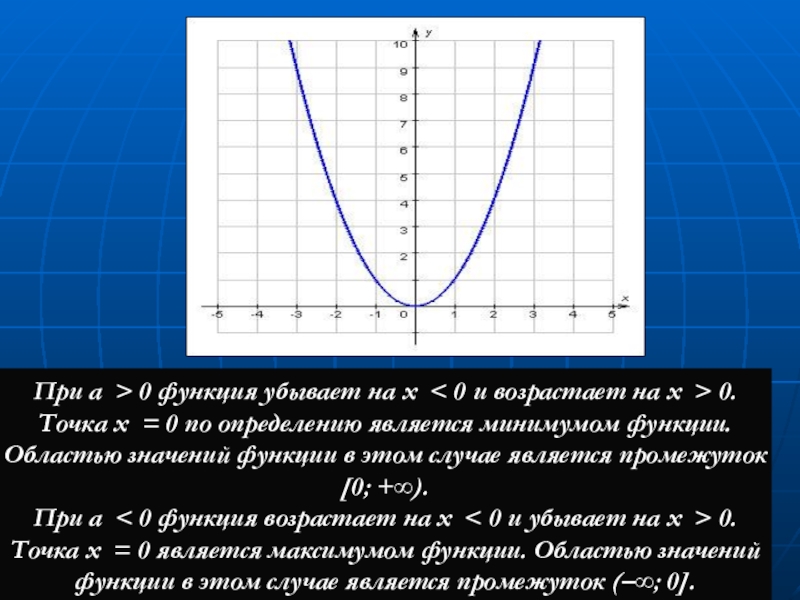
- 20. При a > 0 функция убывает на x
- 21. График функции f ( x ) = ax
- 22. Для этого нужно растянуть график y =
- 23. Точка
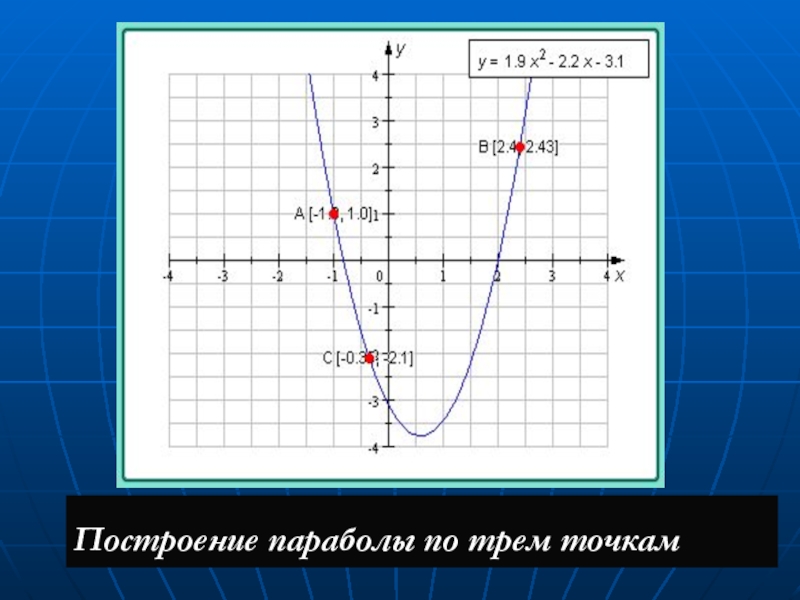
- 24. Построение параболы по трем точкам
- 25. Практикум
- 26. 1. Изобразите схематически график функции:а)
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. 2. График функции
- 31. 3. Для параболы, которая является графиком функции
- 32. 4. Исследуйте функцию и постройте график .
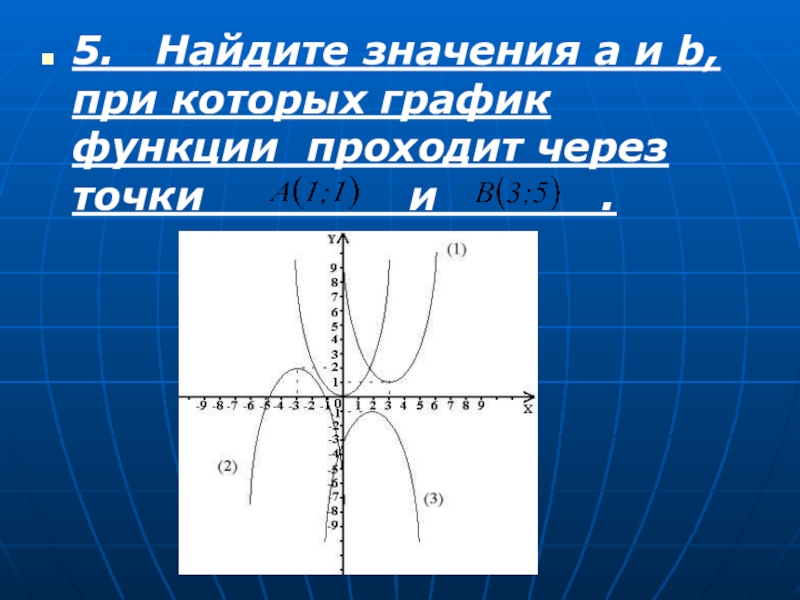
- 33. 5. Найдите значения а и b, при
- 34. 6. Объясните построение графика функции
- 35. Пример 1. Построить график функцииНайти нули функции..
- 36. Алгоритм построения графика квадратной функцииОпределить направление «ветвей» параболы.Вычислить координаты вершины параболы.Записать уравнение оси симметрии.Вычислить несколько точек.
- 37. || ЭТАП АКТУАЛИЗАЦИИ ЗНАНИЙ Изобразите
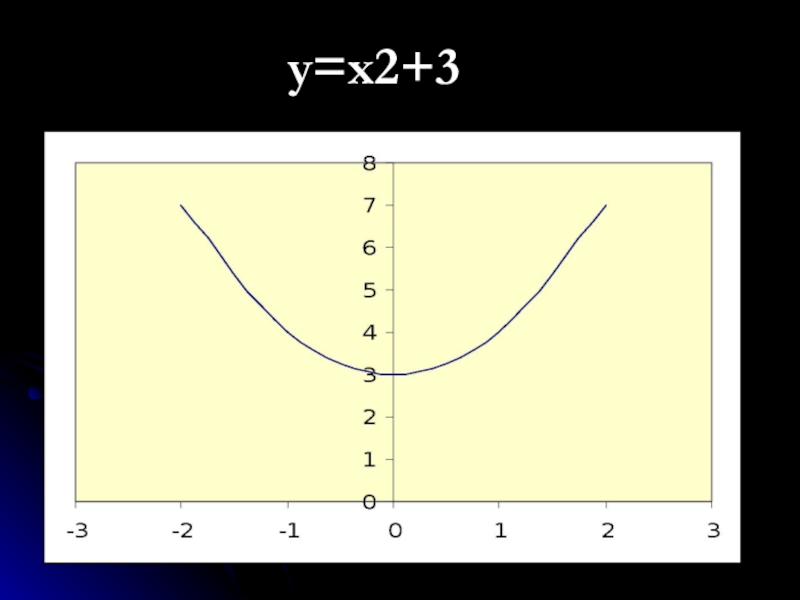
- 38. y=x2+3
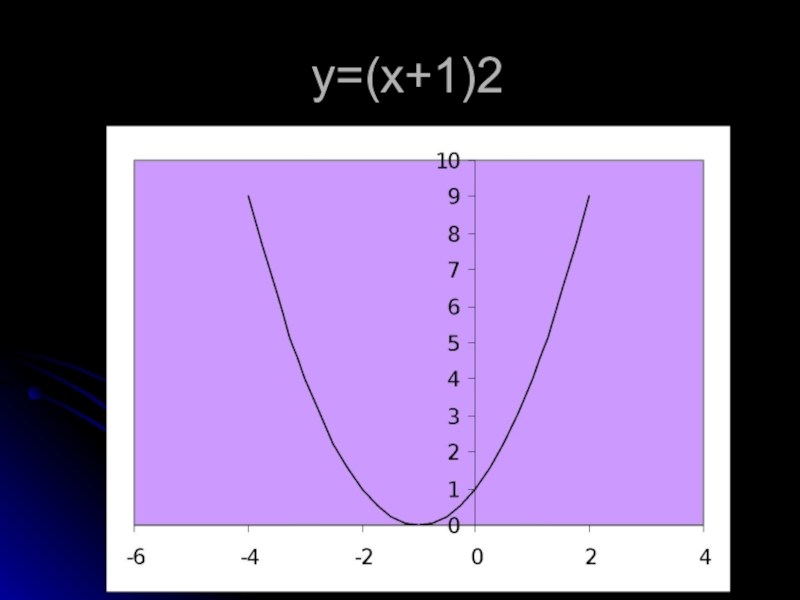
- 39. y=(x+1)2
- 40. y=-x2+2
- 41. Построю графики квадратичной функции, содержащей модуль.1)2)3)4)
- 42. у=2х2-3|х|-2
- 43. у=|(1/2)х2-х|-4
- 44. у=2x|х|-3x+4
- 45. у=х-2x|х|
- 46. Квадратный трехчлен
- 47. Квадратичной называется функция вида y = ax2 + bx + c,где a ≠ 0, b,
- 48. Пусть имеется квадратный трехчлен y = ax2 + bx + c. При решении
- 49. Число дискриминантом квадратного трехчлена. называетсяДискриминант трехчлена x2 + 3x – 2
- 50. Квадратное уравнение
- 51. Уравнение где a ≠ 0, называется квадратным уравнением
- 52. Выделив полный квадрат, получим уравнение Если то
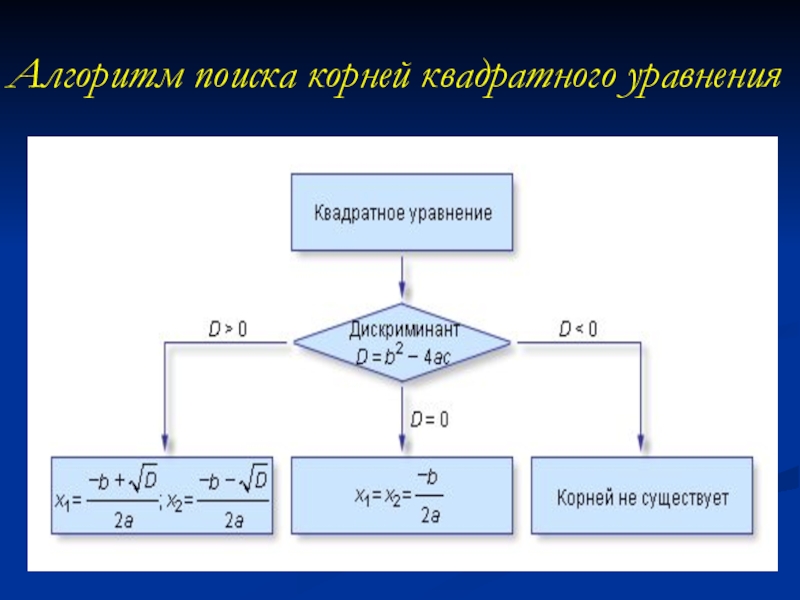
- 53. Алгоритм поиска корней квадратного уравнения
- 54. При D > 0 существуют два корня x1 и
- 55. Если D ≥ 0, то квадратичную функцию можно разложить на множители: Таким образом y = a (x – x1) (x – x2), где
- 56. Если D = 0, то Если D
- 57. Движение по параболе
- 58. Теорема ВиетаПо праву достойна в стихах быть
- 59. Франсуа Виет. Отец современной буквенной
- 60. Теорема Виета. Для того чтобы числа x1
- 61. Доказательство
- 62. Необходимость. Пусть числа и являются корнями уравнения
- 63. 2. Достаточность. Пусть имеется система Из первого
- 64. Задания
- 65. Слайд 65
- 66. Задание 2.Найти все значения параметра а, при
- 67. Задание 3. Найти все значения параметра, при каждом из которых уравнение 4x-a•2x+1-3a2+4a=0 имеет единственный корень.
- 68. Алгоритм решения: исследуем изменение параметра k
- 69. 3 случая
- 70. 1 случайЕсли k-1>0,т.е. k>1, то ветви квадратичной функции f(x)=(k-1)x2+(2k-3)x+k-3 направлены вверх.
- 71. Изобразим на координатной плоскости графики функций в
- 72. 2 случай(k-1)x2+(2k-3)x+k-3>0 если k-1=0 , то k=1Данное
- 73. Рассматриваемая функция будет линейной y=-x-2, графиком является
- 74. 3 случайЕсли k-1
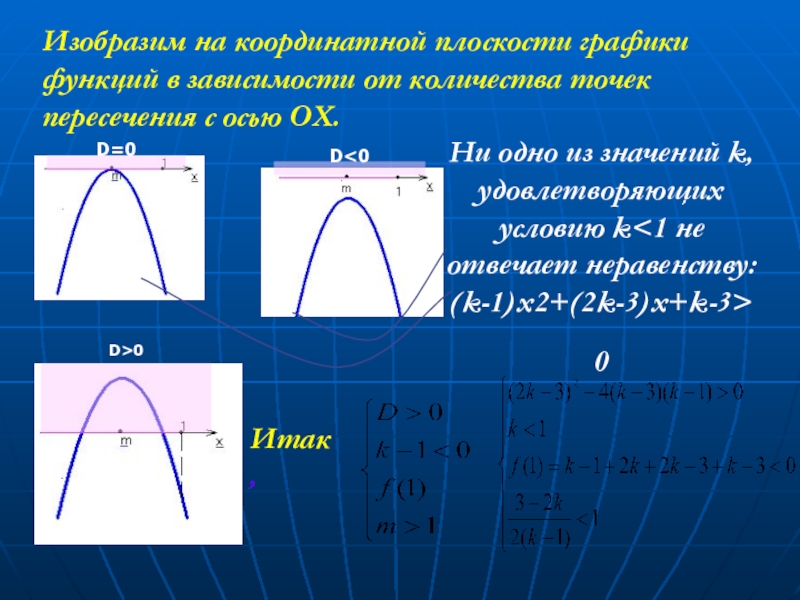
- 75. Изобразим на координатной плоскости графики функций в зависимости от количества точек пересечения с осью OX.D=0D0Итак,
- 76. Решим систему неравенствОтметим решение системы неравенств на координатной прямой:Вывод: при 3/4
- 77. Объединяя найденные значения k, делаем вывод:Утверждение “неравенство
- 78. Найти все значения параметра а, при каждом
- 79. Слайд 79
- 80. ЗАКЛЮЧЕНИЕ
- 81. С квадратичной функцией нам приходилось иметь
- 82. Слайд 82
- 83. Параболу мы часто можем наблюдать в реальной
- 84. В заключении я расскажу
- 85. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением называется эллиптическим параболоидом.
- 86. Поверхность, задаваемая в некоторой прямоугольной декартовой системе
- 87. БИБЛИОГРАФИЧЕСКИЙ список
- 88. Дорофеев Г.В. Математика 9 класс. Алгебра. Функции.
Слайд 2ОГЛАВЛЕНИЕ:
Титульный лист
Оглавление
Введение
Историческая справка
Квадратичная функция
Квадратный трехчлен
Заключение
Слайд 3Введение
Знаете ли вы, что квадратные уравнения умели решать
Слайд 4
…Первобытная мама по имени…впрочем, у неё, наверное, и имени-то не было,
Слайд 5
Пусть х - количество яблок, доставшихся каждому ребёнку. Детей
4х=12 следовательно, х=3.
Слайд 6
Получается, что мама решила задачу на составление уравнения, обойдясь,
Слайд 7
Задачи: изучив литературу по данной теме, исследовать свойства и построение различных
Цели: исследовать квадратичную функцию, её график алгоритм решения различных квадратных уравнений.
Слайд 8
Гипотеза: если исследовать свойства квадратичной функции, ее свойства, графики, алгоритм решения
Объект исследования: квадратичная функция, квадратное уравнение.
Предмет исследования: формулы нахождения дискриминанта и для нахождения корней квадратного уравнения, теорема Виета, графики квадратичной функции, параметры, модуль.
Слайд 10Производство
Вернёмся и мы к квадратным уравнениям. Вспомним самый привычный вид таких
Для решения уравнений такого вида имеем формулу
Зная корни этого уравнения, можем записать его в таком виде:
=0
Слайд 11
А если раскрыть скобки, то из уравнения получим такое уравнение:
По существу все три формы и есть запись одного и того же: дан квадратный трехчлен, при некоторых значениях переменной он становится равными нулю, надо отыскать эти значения. В 1 случае действуем по формуле, в случае 2 корни уже известны – мы еще с пятого класса знаем, что произведение равно нулю тогда, когда хотя бы один множитель равен нулю
Слайд 12
Случай же 3 есть просто другая форма записи уравнения 1. Но
Преобразуя эту систему, можно найти корни, именно так и поступали в Древнем Вавилоне.
Слайд 13
В простейших случаях можно и не выполнять каких-либо преобразований. Например, решая
Вовсе не надо применять формулу. Ведь и без нее ясно, что двумя числами, сумма которых равна 5, а произведение – 6, могут быть только числа 2 и 3.
Слайд 14
Обратимся теперь к четвертому киту школьной алгебры – учению о функции.
Слайд 15
Знаменитый древнегреческий ученый Г е р о д о т (между
Вы можете провести десятки подобных примеров и вместе с нами сказать, что хотя в древности функций еще не знали, но явления, которые мы сегодня описываем с их помощью, давно известны людям.
Слайд 16
Очень важный шаг был сделан в Древнем Вавилоне. Вавилонские мудрецы составили
,
,
,
,
,
и некоторые другие.
Конечно, это еще не были таблицы значений функций в нашем понимании, но все же и здесь каждому значению Х в этих таблицах отвечало единственное число.
Слайд 17
Позднее, в связи с развитием астрономии древнегреческим ученым Г и
В знаменитом сочинении Птолемея «Альмагест» (той самой книге, где изложена геоцентрическая система мира, т.е. та система, по которой в центре Вселенной помещается не Солнце, а Земля) приведены таблицы хорд для углов от 0 до 180
через каждые полградуса (принято говорить «с шагом в полградуса»).
В таблицах Птолемея каждому значению угла соответствует единственное значение хорды, иначе говоря, в них тоже описана некоторая функция.
Слайд 19
График функции при
Слайд 20
При a > 0 функция убывает на x
При a < 0 функция возрастает на x < 0 и убывает на x > 0. Точка x = 0 является максимумом функции. Областью значений функции в этом случае является промежуток (–∞; 0].
Слайд 21
График функции f ( x ) = ax 2 + bx +
Слайд 22
Для этого нужно растянуть график y = x 2 в a
этих чисел меньше нуля, то соответствующее смещение нужно производить в противоположную сторону).
Слайд 23
Точка является точкой
Если a < 0, то в этой точке достигается максимум функции, и
Функция f ( x ) = ax 2 + bx + c при b = 0 является четной, а в общем случае уже не является ни четной, ни нечетной.
Слайд 30
2. График функции
Слайд 31
3. Для параболы, которая является графиком функции
а) направление ветвей;
б) координаты вершины;
в) координаты точек пересечения с осями.
Слайд 346. Объясните построение графика функции 1). Строим график функции 2). Симметрично поднимаем
Слайд 35
Пример 1. Построить график функции
Найти нули функции.. Решение.
1) Направление «ветвей» параболы:
2) Координаты вершины параболы: ,
3) Уравнение оси симметрии: х=3.
4) Нули функции:
Слайд 36Алгоритм построения графика квадратной функции
Определить направление «ветвей» параболы.
Вычислить координаты вершины параболы.
Записать
Вычислить несколько точек.
Слайд 37|| ЭТАП АКТУАЛИЗАЦИИ ЗНАНИЙ Изобразите схематически график функции и укажите область
Слайд 47
Квадратичной называется функция вида
y = ax2 + bx + c,
где a ≠ 0, b, c – любые действительные
Примерами квадратичных функций являются y = x2 + 3x – 2, y = –x2 + 4x, y = 2x2 + 5.
Выражение ax2 + bx + c, a ≠ 0 называют квадратным трехчленом.
Слайд 48
Пусть имеется квадратный трехчлен y = ax2 + bx + c. При решении многих задач полезным приемом
Так, x2 + 2x – 2 = (x + 1)2 – 3, 3x2 – 12x = 3 (x – 2)2 – 12.
Слайд 49
Число
дискриминантом квадратного трехчлена.
называется
Дискриминант трехчлена x2 + 3x – 2 равен 32 – 4 · 1(–2) = 17, трехчлена –x2 + 4x
Слайд 52
Выделив полный квадрат, получим уравнение
Если
то отсюда следует, что
или
Мы получили формулу корней квадратного уравнения (формулу Виета).
Слайд 54
При D > 0 существуют два корня x1 и x2. При D = 0 корни
невозможно, и корней у квадратного уравнения не существует.
Слайд 55
Если D ≥ 0, то квадратичную функцию можно разложить на множители:
Таким образом
y = a (x – x1) (x – x2),
где
Слайд 58Теорема Виета
По праву достойна в стихах быть воспета
О свойствах корней теорема
Что лучше скажи, постоянства такого:
Умножишь ты корни - и дробь уж готова.
В числителе «с», в знаменателе «а».
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта,
Что за беда – В числителе «b», в знаменателе «а».
Слайд 59
Франсуа Виет. Отец современной буквенной алгебры. А между тем,
Слайд 60
Теорема Виета. Для того чтобы числа x1 и x2 были корнями
Слайд 63
2. Достаточность. Пусть имеется система
Из первого равенства
Подставляя это значение
откуда
Значит, число
является корнем квадратного
Аналогично доказывается, что
– также корень этого уравнения.
уравнения
Слайд 65
Слайд 66
Задание 2.
Найти все значения параметра а, при
каждом из которых корни
трёхчлена x2 +ax+1 различны и лежат
на отрезке [0;2]?
Слайд 67
Задание 3.
Найти все значения параметра, при каждом из которых уравнение
Слайд 70
1 случай
Если k-1>0,т.е. k>1,
то ветви квадратичной функции
f(x)=(k-1)x2+(2k-3)x+k-3 направлены вверх.
Слайд 71
Изобразим на координатной плоскости графики функций в зависимости от количества точек
т. к. решаем неравенство (k-1)x2+(2k-3)x+k-3>0, то
покажем решение в верхней полуплоскости.
Вывод: при k>1 всегда найдутся значения x<1, при которых выполняется данное неравенство
Слайд 72
2 случай
(k-1)x2+(2k-3)x+k-3>0
если k-1=0 , то k=1
Данное неравенство
(k-1)x2+(2k-3)x+k-3>0
примет вид:
-x>2,
x<-2
Слайд 73
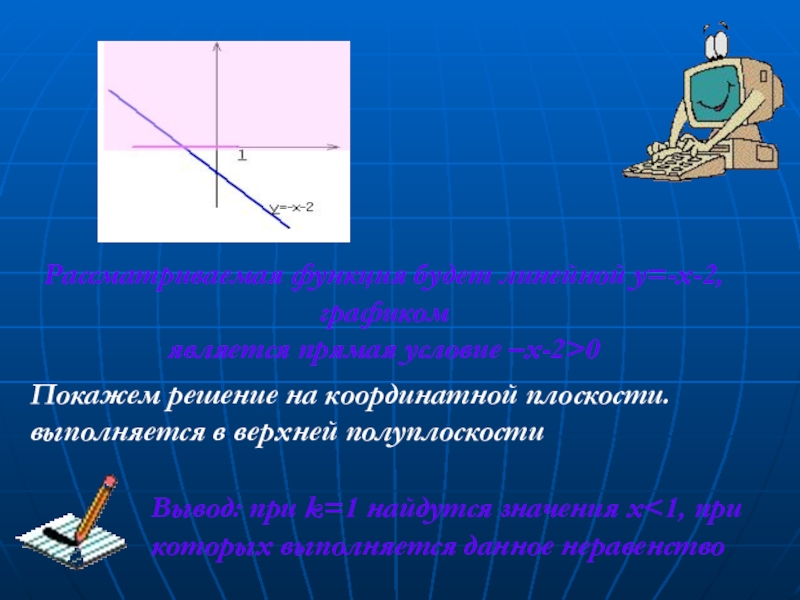
Рассматриваемая функция будет линейной y=-x-2, графиком
является прямая условие –x-2>0
Покажем решение
Вывод: при k=1 найдутся значения x<1, при которых выполняется данное неравенство
Слайд 75
Изобразим на координатной плоскости графики функций в зависимости от количества точек
D=0
D<0
Ни одно из значений k, удовлетворяющих условию k<1 не отвечает неравенству:
(k-1)x2+(2k-3)x+k-3>0
D>0
Итак,
Слайд 76
Решим систему неравенств
Отметим решение системы неравенств на координатной прямой:
Вывод: при 3/4
Слайд 77
Объединяя найденные значения k,
делаем вывод:
Утверждение
“неравенство (k-1)x2+(2k-3)x+k-3>0 выполняется хотя бы
при k>1 k>3/4. Ответ: при k >3/4
при k=1
при 3/4
неравенство (k-1)x2+(2k-3)x+k-3>0
выполняется хотя бы при одном x<1.
Слайд 78
Найти все значения параметра а, при каждом из которых корни квадратного
Решение.
Рассмотрим функцию f(x)= x2 +ax+1
Оценим значения:
D
Положение
вершины
параболы
Коэффициент
при x2
для существования различных корней необходимо выполнение условия
D>0
т.е. a2-4>0 или
a<-2 и a>2,
внутри отрезка [0;2] т.е. 0<-a/2<2
положителен, то f(2)= 2a+5>0
Ответ:
корни квадратного трёхчлена x2 +ax+1 различны и лежат на отрезке [0;2] при
-a/2
Слайд 81
С квадратичной функцией нам приходилось иметь дело при работе с
Слайд 83
Параболу мы часто можем наблюдать в реальной жизни как траекторию движения
Слайд 84
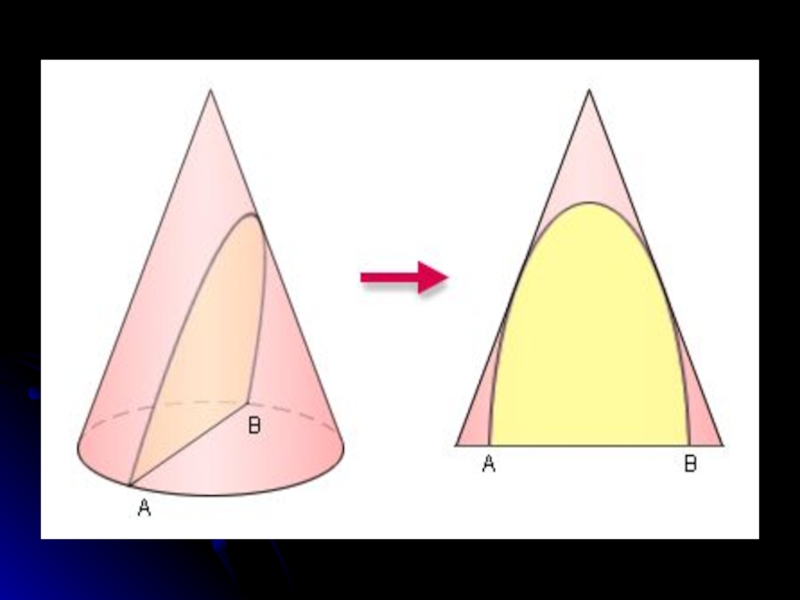
В заключении я расскажу об одном важном свойстве
Слайд 85Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется эллиптическим параболоидом.
Слайд 86Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
Слайд 88
Дорофеев Г.В. Математика 9 класс. Алгебра. Функции. Анализ данных М., 2004
Дорофеев Г.В. Математика 8 класс. М., 2004 г..
Глейзер Г.И. История математики в школе. М., 1982г..
Подольский В.А., Суходский А.М. Сборник задач по математике. М., стр. 50
Пичурин Л.Ф. За страницами учебника алгебры. М., 1990 г..