- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Квадратичная функция (9 класс)
Содержание
- 1. Презентация по алгебре на тему Квадратичная функция (9 класс)
- 2. ЦельНаучиться по формуле квадратичной функции определять положение и форму соответствующей параболы
- 3. y = ax²+ bx + c – квадратичная функцияa,b,c – коэффициентыb,c – любые числаа ≠ 0
- 4. Функция у = х²График строится по точкам,
- 5. Функция у = ах²1) а > 0
- 6. Функция у = ах² + n1) n
- 7. Функция у = а (х – m)²1)
- 8. Функция у = а (х – m)²
- 9. ВыводФорма параболы задаётся абсолютной величиной коэффициента
- 10. Информационные ресурсы1.Ю.Н. Макарычев и др.»Алгебра.9» Москва.» Просвещение»
Слайд 1Построение графиков квадратичной функции
АВТОРЫ:
Лебедев Артем, ученик 9 класса
Учитель: Лебедева Елена
Слайд 2Цель
Научиться по формуле квадратичной функции определять положение и форму соответствующей параболы
Слайд 4Функция у = х²
График строится по точкам, координаты которых рассчитываем по
График – парабола.
Парабола у = х² является основой для построения графиков функций более сложного вида.
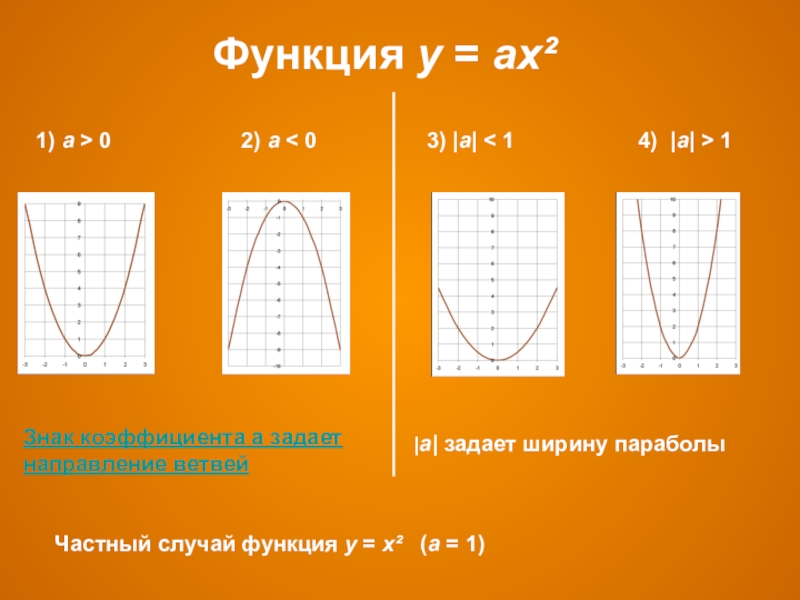
Слайд 5Функция у = ах²
1) а > 0
3) |а| < 1 4) |а| > 1
Знак коэффициента а задает направление ветвей
|а| задает ширину параболы
Частный случай функция у = х² (а = 1)
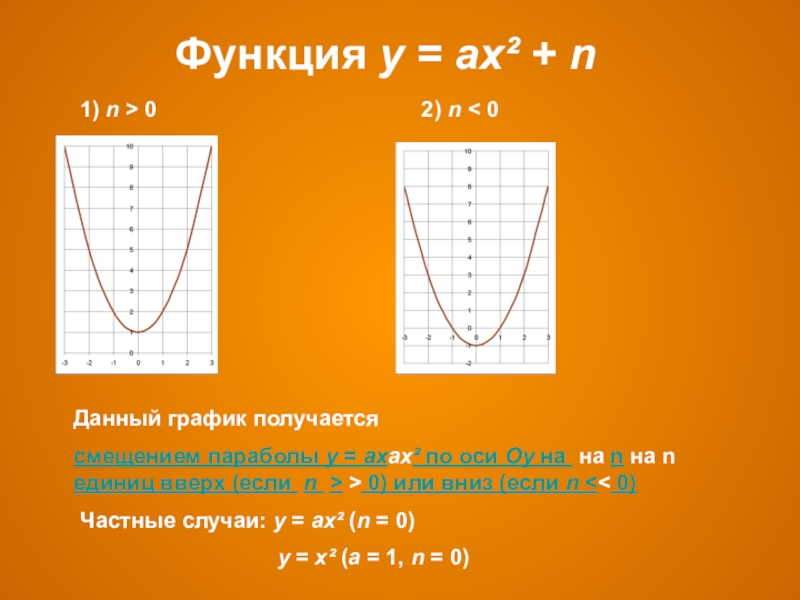
Слайд 6Функция у = ах² + n
1) n > 0
Данный график получается
смещением параболы у = ахах² по оси Оу на на n на n единиц вверх (если n > > 0) или вниз (если n << 0)
Частные случаи: у = ах² (n = 0)
у = х² (а = 1, n = 0)
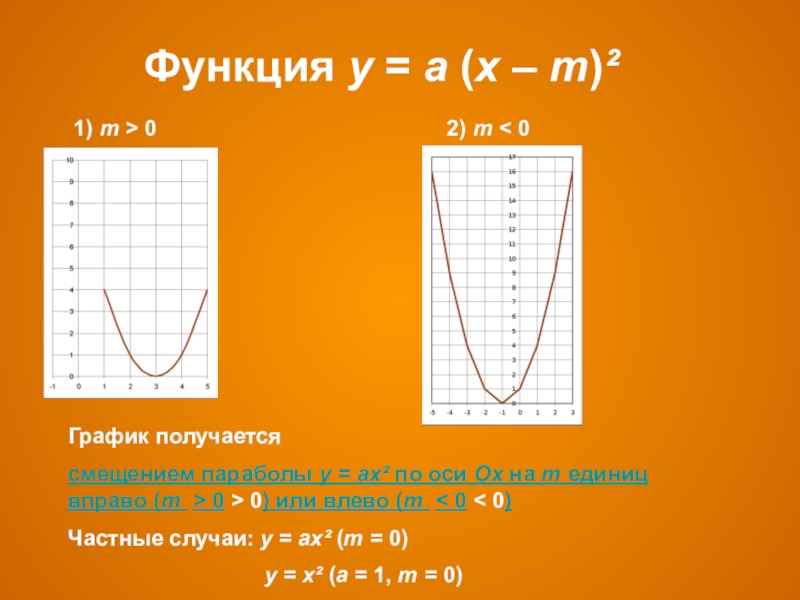
Слайд 7Функция у = а (х – m)²
1) m > 0
График получается
смещением параболы у = ах² по оси Ох на m единиц вправо (m > 0 > 0) или влево (m < 0 < 0)
Частные случаи: у = ах² (m = 0)
у = х² (а = 1, m = 0)
Слайд 8
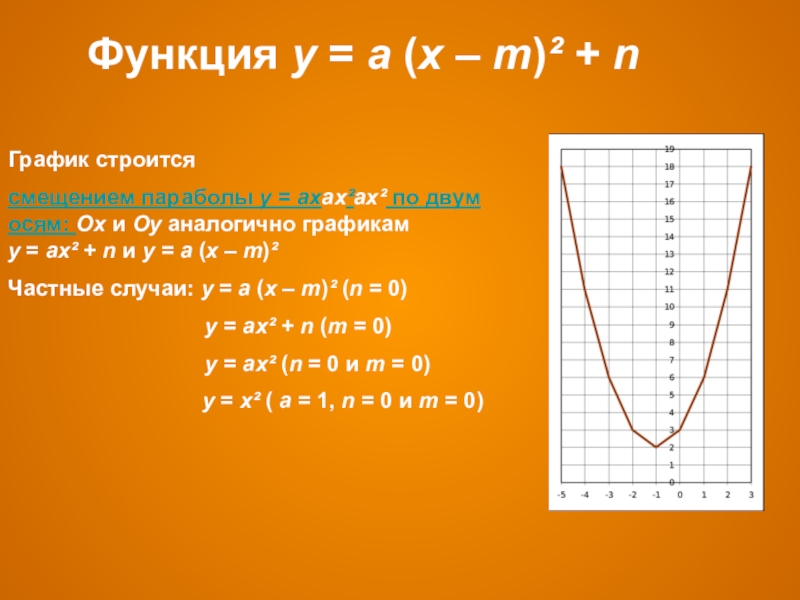
Функция у = а (х – m)² + n
График строится
смещением
Частные случаи: у = а (х – m)² (n = 0)
у = ах² + n (m = 0)
у = ах² (n = 0 и m = 0)
у = х² ( а = 1, n = 0 и m = 0)
Слайд 9Вывод
Форма параболы задаётся абсолютной величиной коэффициента а.
Направление ветвей зависит от
Положение параболы относительно начала координат определяется коэффициентами m и n.