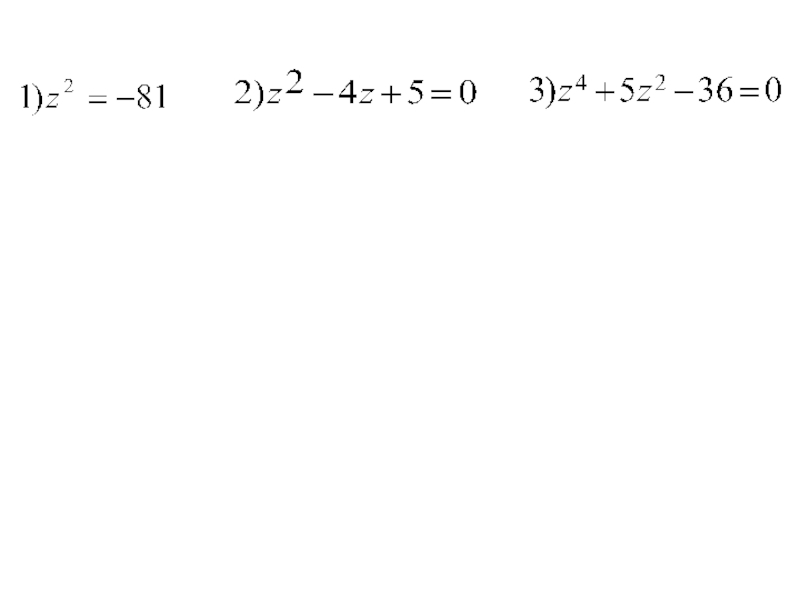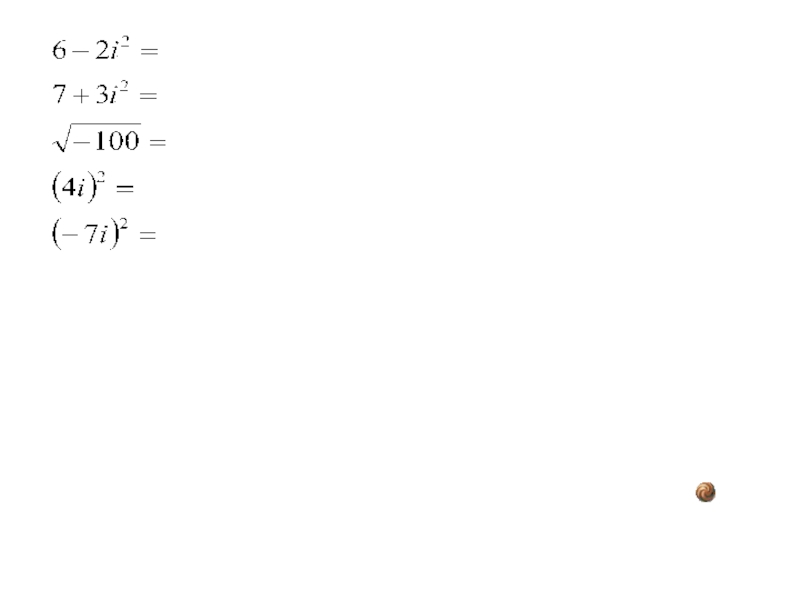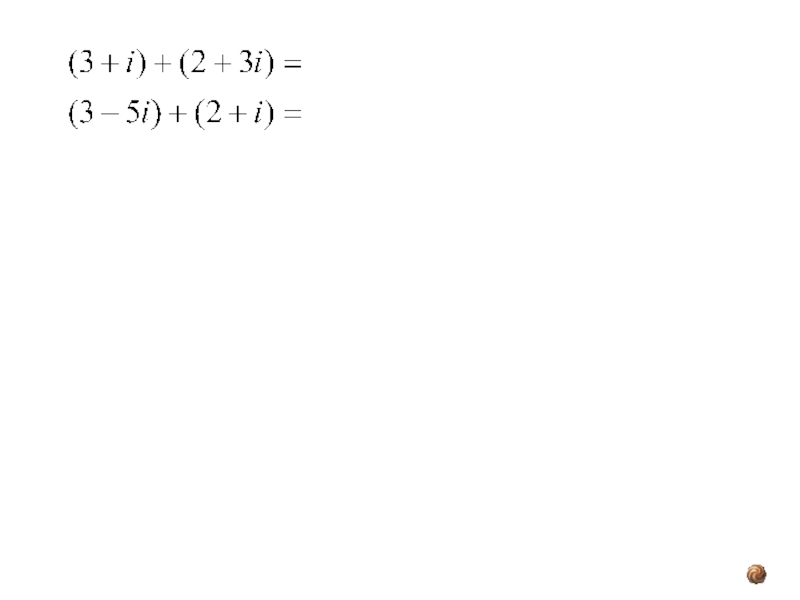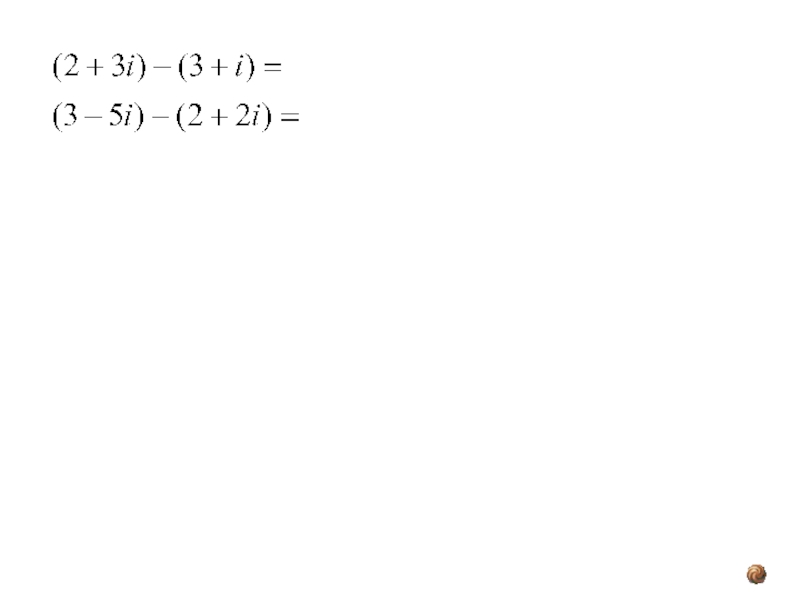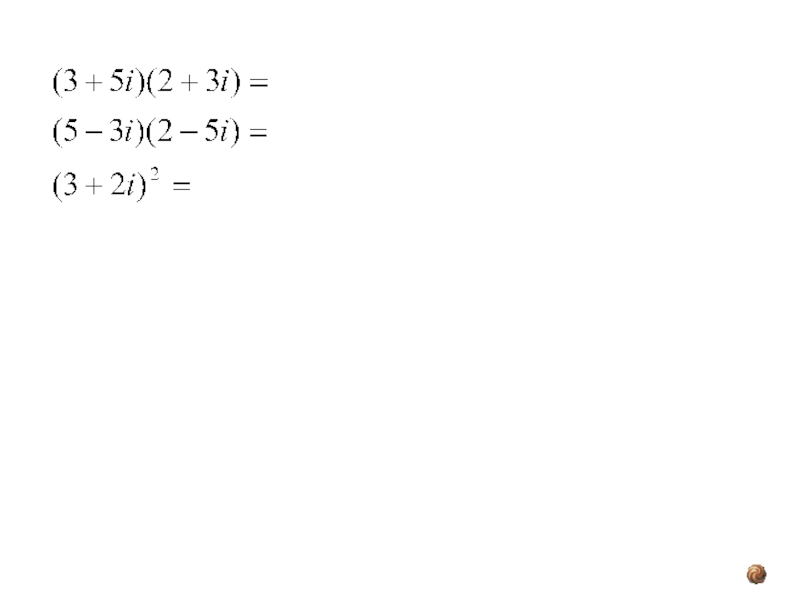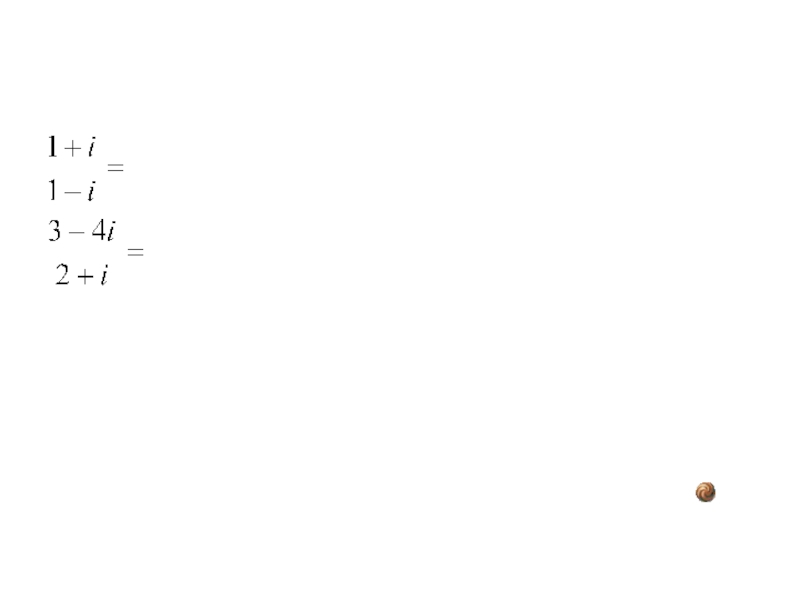- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Комплексные числа (10-11 класс)
Содержание
- 1. Презентация по алгебре на тему Комплексные числа (10-11 класс)
- 2. а в 1777г. один из крупнейших математиков
- 3. Комплексные числа – это выражения вида a
- 4. Число а называется действительной частью комплексного числа
- 5. Два комплексных числа a + bi и
- 6. Слайд 6
- 7. Вычитание комплексных чисел (а+bi) - (c+di) =
- 8. Для умножения комплексных чисел также справедливы
- 9. Деление комплексных чисел (кроме деления на нуль)
- 10. Квадратное уравнение может не иметь действительных корней.
- 11. Примеры:z2=-9 z2=a, где a
- 12. Слайд 12
- 13. продолжение следует
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
а в 1777г. один из крупнейших математиков VIII века Х. Эйлер предложил использовать первую букву французского числа i = (мнимой единицы)Название «мнимые числа» ввел в 1637г. французский математик и философ Р. ДекартЭтот
Слайд 2
а в 1777г. один из крупнейших математиков VIII века Х. Эйлер
предложил использовать первую букву французского числа i = (мнимой единицы)
Название «мнимые числа» ввел в 1637г. французский математик и философ Р. Декарт
Этот символ вошел во всеобщее употребление благодаря К. Гауссу (1831г).
Слайд 3Комплексные числа – это выражения вида a + bi, где
a и b – действительные числа,
i- такое число, что i 2=-1
Примеры: 3 +2i , 5-7i , -4+3i
Отметим тот факт, что знак ( + ) в написанном выражении a + bi не есть знак действия.
Это выражение надо рассматривать как единый символ для обозначения комплексного числа.
Итак: i 2 = -1
= i
i- такое число, что i 2=-1
Примеры: 3 +2i , 5-7i , -4+3i
Отметим тот факт, что знак ( + ) в написанном выражении a + bi не есть знак действия.
Это выражение надо рассматривать как единый символ для обозначения комплексного числа.
Итак: i 2 = -1
= i
Примеры: 2 i 2 = -2
-5 i 2= 5
Слайд 4Число а называется действительной частью комплексного числа a + bi, а
число b –его мнимой частью.
Пример: комплексное число 2 + 3i,
его действительная часть равна 2,
мнимая часть равна 3.
Действительные числа являются частными случаями комплексных чисел.
Пример:
2 = 2+0•i
0= 0+0•i
-4= -4+0•i
Слайд 5Два комплексных числа a + bi и c + di называют
равными, если a=c и b=d, т.е. если равны их действительные и мнимые части.
Пример:
Арифметические действия над комплексными числами определяют так, чтобы все свойства этих действий были такими же, как и для действительных чисел. Поэтому действия над комплексными числами a + bi можно выполнять так же, как и действия над многочленами, считая, что i 2 =-1
Пример:
Арифметические действия над комплексными числами определяют так, чтобы все свойства этих действий были такими же, как и для действительных чисел. Поэтому действия над комплексными числами a + bi можно выполнять так же, как и действия над многочленами, считая, что i 2 =-1
Слайд 6 Суммой двух комплексных
чисел
(a + bi )+(c + di ) = (a+c) + (b+d)i.
Пример: (4-3i)+(-2+7i)=4-3i-2+7i=2+4i
Числа a+bi и a-bi называются сопряженными.
(а+bi) + (а-bi) = 2а , где 2а - действительное число
Числа а+bi и -a-bi называются противоположными.
(a + bi )+(c + di ) = (a+c) + (b+d)i.
Пример: (4-3i)+(-2+7i)=4-3i-2+7i=2+4i
Числа a+bi и a-bi называются сопряженными.
(а+bi) + (а-bi) = 2а , где 2а - действительное число
Числа а+bi и -a-bi называются противоположными.
(а+bi) + (-а-bi) =0
Слайд 7Вычитание комплексных чисел
(а+bi) - (c+di) = (a-c) + (b-d)i.
Пример: (8-5i)-(9-4i)=8-5i-9+4i=-1-i
Произведение комплексных чисел
z1= a + bi и z2 = c + di
называется комплексное число
z = (ac-bd) + (ad + bc)i,
Произведение комплексных чисел
z1= a + bi и z2 = c + di
называется комплексное число
z = (ac-bd) + (ad + bc)i,
Слайд 8 Для умножения комплексных чисел также справедливы переместительный и сочетательный законы,
а также распределительный закон умножения по отношению к сложению.
Пример: (2+i)•(1-3i)=2-6i+i-3i²=2-5i-3•(-1)=5-5i
Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу:
(a + bi)(a - bi) = a² + b²
Пример: (2+i)•(1-3i)=2-6i+i-3i²=2-5i-3•(-1)=5-5i
Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу:
(a + bi)(a - bi) = a² + b²
Слайд 9Деление комплексных чисел
(кроме деления на нуль)
определяется как действие, обратное
умножению.
Пример:
5-14i
2-3i
10+15i-28i-42i 2
4-32i 2
52-13i
13
4 -i
Слайд 10Квадратное уравнение может не иметь действительных корней. Простейшим из таких уравнений
является уравнение x²+1=0.
Чтобы любое квадратное уравнение имело корни, приходится расширять множество действительных чисел и эти новые числа вместе с действительными образуют множество, которое называют множеством комплексных чисел.
Если комплексные числа введены, то квадратное уравнение х²+1=0 имеет корень. Этот корень обозначают буквой i (мнимой единицей).
Чтобы любое квадратное уравнение имело корни, приходится расширять множество действительных чисел и эти новые числа вместе с действительными образуют множество, которое называют множеством комплексных чисел.
Если комплексные числа введены, то квадратное уравнение х²+1=0 имеет корень. Этот корень обозначают буквой i (мнимой единицей).
