- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Графы.Полный граф.Граф-дерево
Содержание
- 1. Презентация по алгебре на тему Графы.Полный граф.Граф-дерево
- 2. Графы представляют собой:абстрактный математический объект, представляющий собой
- 3. Это по сути граф. Пять компьютеров являются
- 4. Полный граф: простой неориентированный граф, в котором
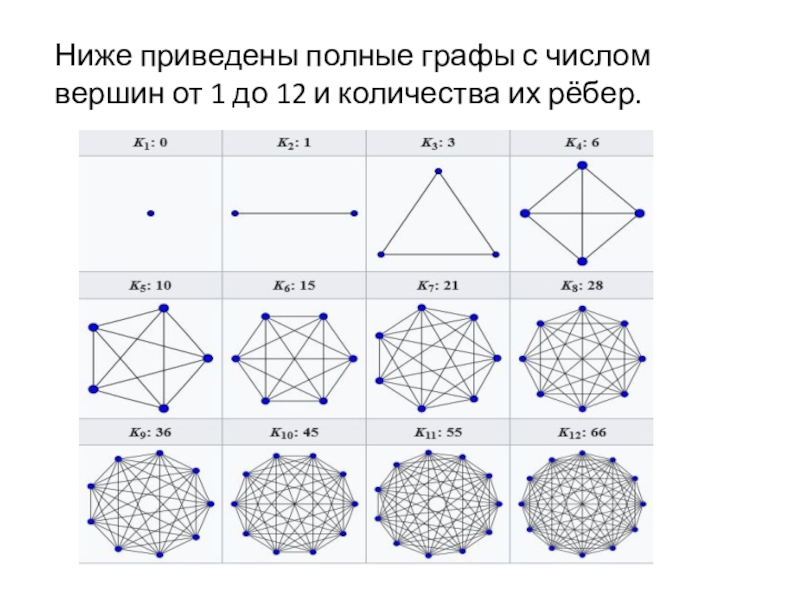
- 5. Ниже приведены полные графы с числом вершин
- 6. Граф дерево: Дерево — это связный
- 7. T — множество узлов дерева, на уровне
- 8. А это графовое дерево:
Графы представляют собой:абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин. Например, за множество вершин можно взять множество аэропортовОпределениеДва ребра называются смежными, если они имеют общую вершину. Два
Слайд 2Графы представляют собой:
абстрактный математический объект, представляющий собой множество вершин графа и
набор рёбер, то есть соединений между парами вершин. Например, за множество вершин можно взять множество аэропортов
Определение
Два ребра называются смежными, если они имеют общую вершину. Два ребра называются кратными, если они соединяют одну и ту же пару вершин. Ребро называется петлей, если его концы совпадают. Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды). Вершина называется изолированной, если она не является концом ни для одного ребра. Вершина называется висячей, если из неё выходит ровно одно ребро.
Определение
Два ребра называются смежными, если они имеют общую вершину. Два ребра называются кратными, если они соединяют одну и ту же пару вершин. Ребро называется петлей, если его концы совпадают. Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды). Вершина называется изолированной, если она не является концом ни для одного ребра. Вершина называется висячей, если из неё выходит ровно одно ребро.
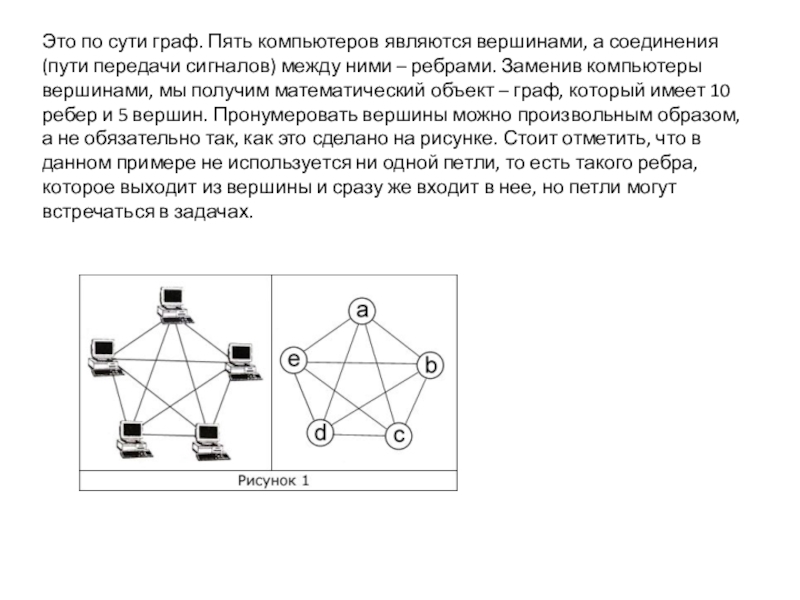
Слайд 3Это по сути граф. Пять компьютеров являются вершинами, а соединения (пути
передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.
Слайд 4Полный граф:
простой неориентированный граф, в котором каждая пара различных вершин
смежна. Полный граф с n
вершинами имеет
n ( n − 1 ) / 2 рёбер и обозначается
K n. Является регулярным графом степени
n − 1.
Полный граф образуется из вершин и ребер (n-1)-симплекса.
По́лный ориенти́рованный граф — ориентированный граф, в котором каждая пара различных вершин соединена парой дуг (с различными направлениями).
вершинами имеет
n ( n − 1 ) / 2 рёбер и обозначается
K n. Является регулярным графом степени
n − 1.
Полный граф образуется из вершин и ребер (n-1)-симплекса.
По́лный ориенти́рованный граф — ориентированный граф, в котором каждая пара различных вершин соединена парой дуг (с различными направлениями).
Слайд 6Граф дерево: Дерево — это связный ациклический граф.[1] Связность означает наличие путей
между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.
Лес — упорядоченное множество упорядоченных деревьев.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.
Связанные определения[править | править код]
Степень вершины — количество инцидентных ей ребер.
Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).
Узел ветвления — неконцевой узел.
Дерево с отмеченной вершиной называется корневым деревом.
Слайд 7T — множество узлов дерева, на уровне m от корня дерева. частичный
порядок на вершинах:
u ≺ v, если вершины u и
v различны и вершина
u лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной v.
корневое поддерево с корнем
v — подграф
{ v } ∪ { w ∣ v < w }.
В контексте, где дерево предполагается имеющим корень, дерево без выделенного корня называется свободным.
Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:
уровень корня дерева T равен 0;
уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева T
, содержащего данный узел.
Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
Несводимым называется дерево, в котором нет вершин степени 2.
Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.



![Презентация по алгебре на тему Графы.Полный граф.Граф-дерево Граф дерево: Дерево — это связный ациклический граф.[1] Связность означает наличие Граф дерево: Дерево — это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин,](/img/thumbs/28569759bd85ee7a8a75a88e9fc8ae64-800x.jpg)







