- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему: Графики функции
Содержание
- 1. Презентация по алгебре на тему: Графики функции
- 2. Определение функции Функция – это зависимость переменной
- 3. Область определения функции – все значения независимой
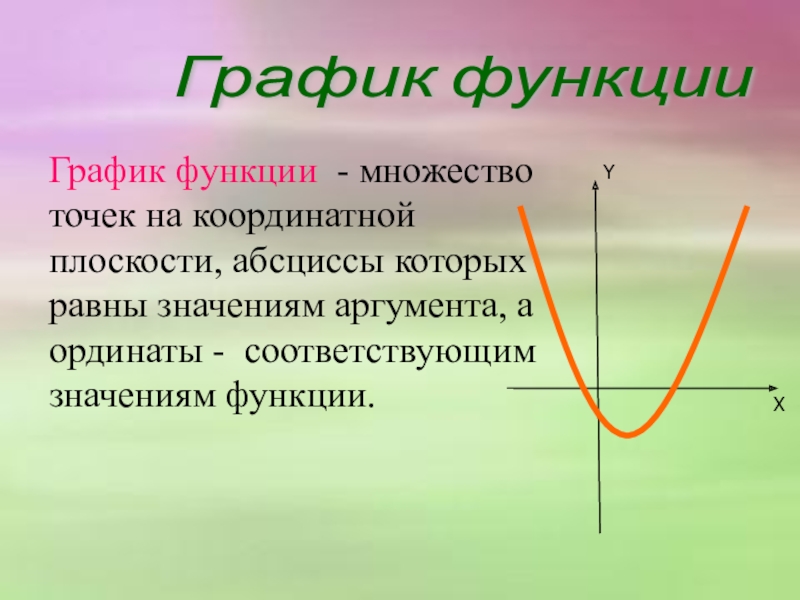
- 4. График функции - множество точек на координатной
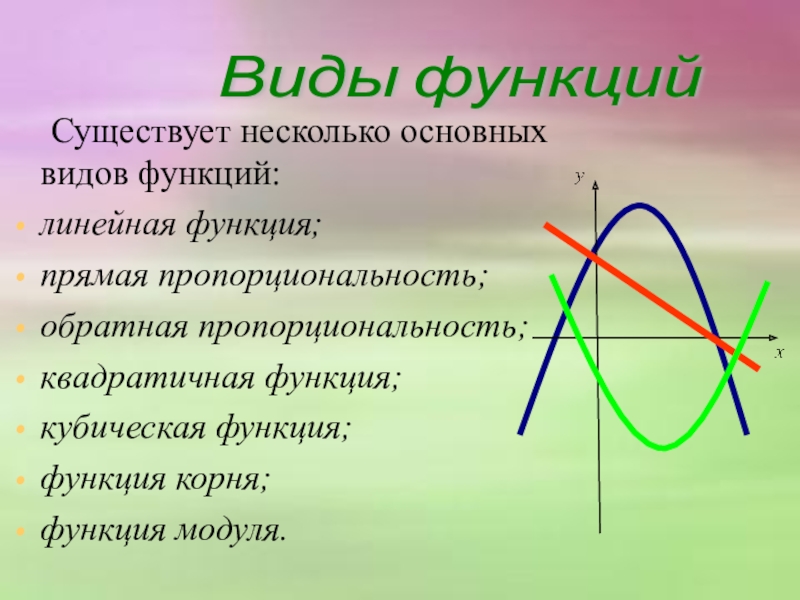
- 5. Существует несколько основных видов функций:линейная функция;прямая пропорциональность;обратная пропорциональность;квадратичная функция;кубическая функция;функция корня;функция модуля.Виды функций
- 6. Линейная функция функция вида y = k
- 7. функция вида y = k х1.
- 8. Обратная пропорциональность функция вида y =
- 9. Квадратичная функция функция вида y = x²
- 10. функция вида y = x³; 1.
- 11. функция вида y = ;
- 12. функция вида y = |x|; 1. D(
- 13. Задание №5 ОГЭ Модуль «Алгебра»
- 14. Графики различных функций Установите соответствие между графиками
- 15. Каждый график соотнесите с соответствующей ему
- 16. Установите соответствия между функциями и их графиками
- 17. 2. Каждую прямую соотнесите с её уравнением:1)x=
- 18. Особенности расположения графика линейной функции Если k>0
- 19. График обратной пропорциональности Установите соответствие между графиками
- 20. График обратной пропорциональности Установите соответствие между графиками
- 21. Особенности расположения графика функции обратной пропорциональностиЕсли k>0
- 22. Как установить соответствие между графиками функций и
- 23. -Если а< 0 и b>0, то
- 24. Установите соответствия между функциями и графикамиФункции А)y=−X2 +2x+5
- 25. Нахождение значения коэффициента а по графику квадратичной
- 26. Нахождение коэффициента b по графику квадратичной функции1)Находим
- 27. Нахождение коэффициента с по графику квадратичной
- 28. УХ101 Проверь себя
Слайд 2Определение функции
Функция – это зависимость переменной у от переменной х,
х – независимая переменная или аргумент
у – зависимая переменная или значение функции
Слайд 3Область определения функции – все значения независимой переменной х.
Обозначение: D( f
Область значений функции – все значения зависимой переменной у.
Обозначение: Е( f )
Если функция у = f(х) задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений х, при которых выражение f(х) имеет смысл.
Слайд 4График функции - множество точек на координатной плоскости, абсциссы которых равны
График функции
X
Y
Слайд 5 Существует несколько основных видов функций:
линейная функция;
прямая пропорциональность;
обратная пропорциональность;
квадратичная функция;
кубическая функция;
функция корня;
функция
Виды функций
Слайд 6Линейная функция
функция вида y = k х + b
1.
E( f ) = R;
графиком функции является прямая
k>0
k<0
k=0
Слайд 7 функция вида y = k х
1. D( f ) =
E( f ) = R;
графиком функции является прямая, проходящая через начало координат.
Прямая пропорциональность
Слайд 8Обратная пропорциональность
функция вида y = ;
1.
2. E( f ) = (-∞;0) (0;∞);
3. графиком функции является гипербола
k
x
k>0
k<0
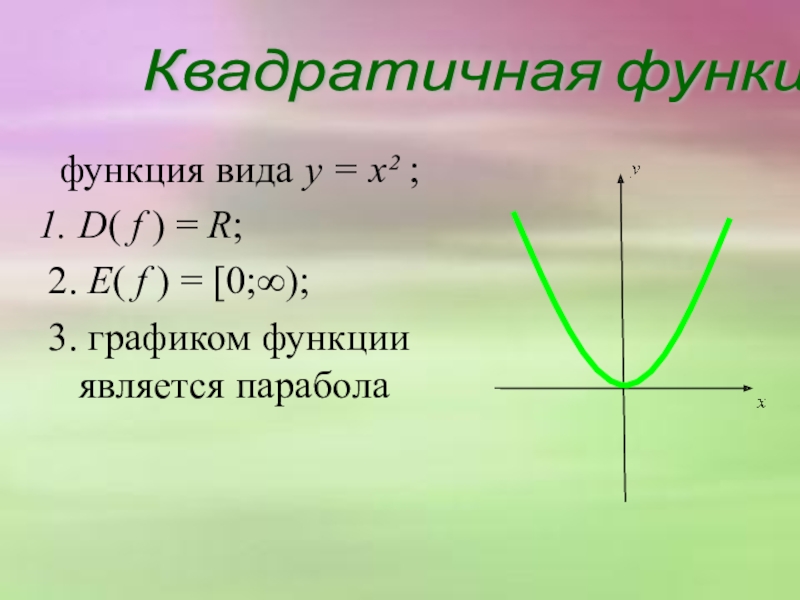
Слайд 9Квадратичная функция
функция вида y = x² ;
D( f
2. E( f ) = [0;∞);
3. графиком функции является парабола
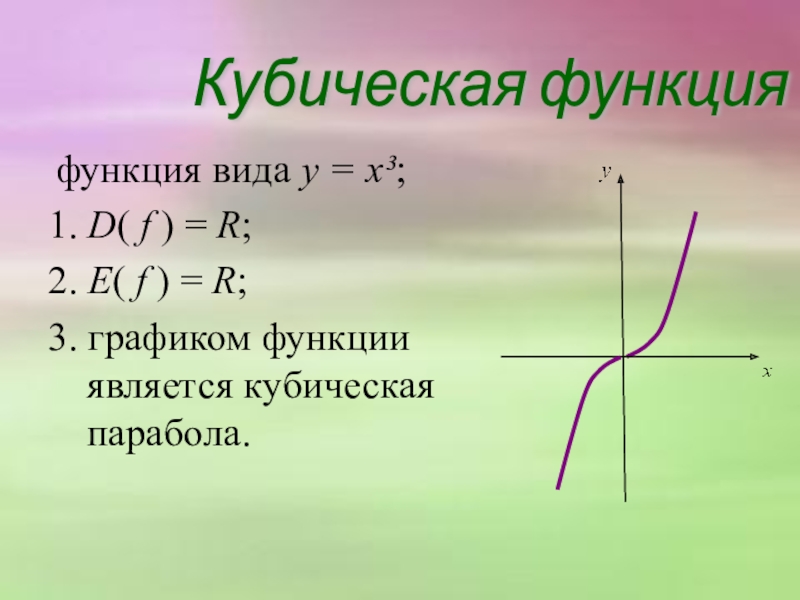
Слайд 10 функция вида y = x³;
1. D( f ) =
2. E( f ) = R;
3. графиком функции является кубическая парабола.
Кубическая функция
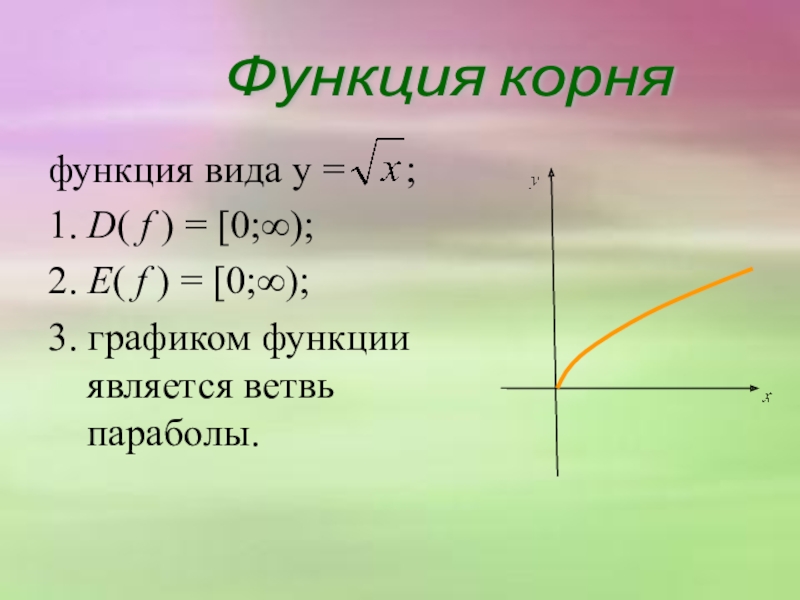
Слайд 11функция вида y = ;
1. D( f )
2. E( f ) = [0;∞);
3. графиком функции является ветвь параболы.
Функция корня
Слайд 12функция вида y = |x|;
1. D( f ) = R;
2. E( f ) = [0;∞);
3. график функции на промежутке [0;∞) совпадает с графиком функции у = х, а на промежутке (-∞;0] – с графиком функции у = -х
График-два луча, являющихся биссектриссами 1 и 2 четверти
Функция модуля
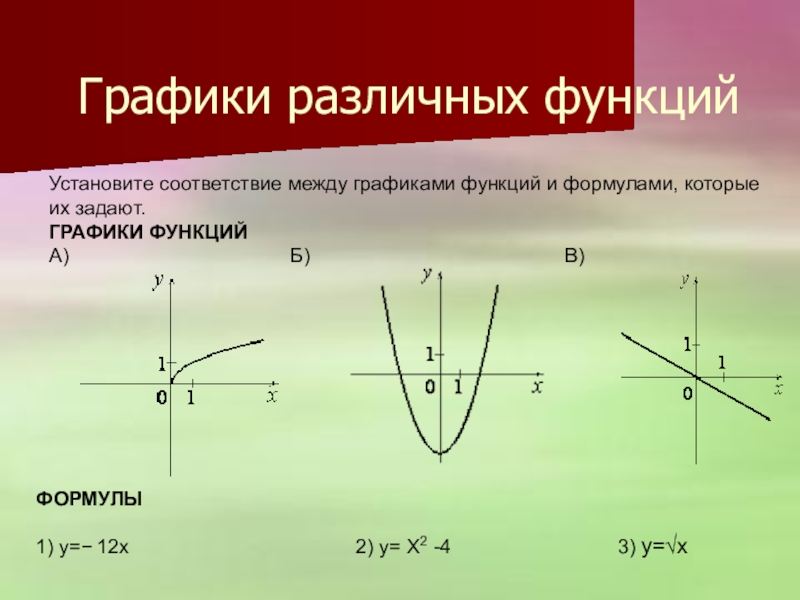
Слайд 14Графики различных функций
Установите соответствие между графиками функций и формулами, которые
ГРАФИКИ ФУНКЦИЙ
А) Б) В)
ФОРМУЛЫ
1) y=− 12x 2) y= X2 -4 3)
y=√x
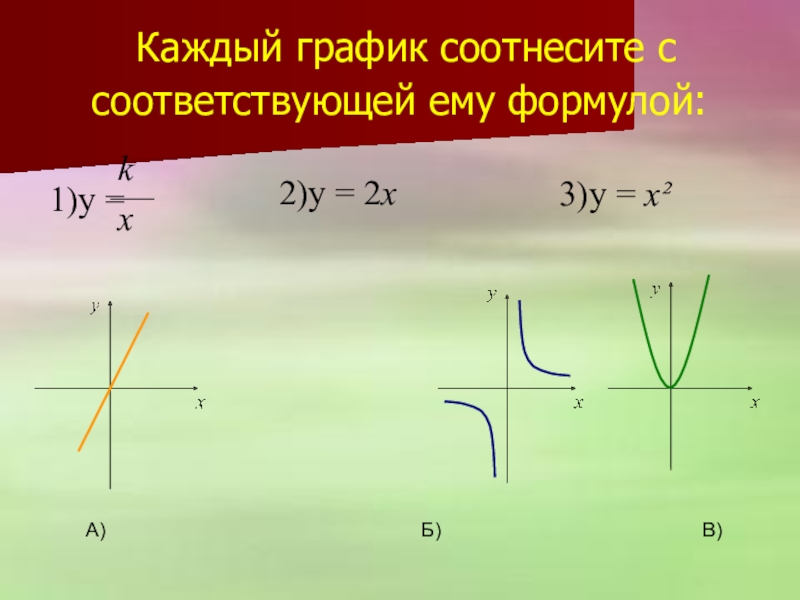
Слайд 15 Каждый график соотнесите с соответствующей ему формулой:
1)y =
k
x
3)y
2)y = 2x
А) Б) В)
Слайд 16Установите соответствия между функциями и их графиками
Функции
А)y=-3x
Графики
1) 2) 3)
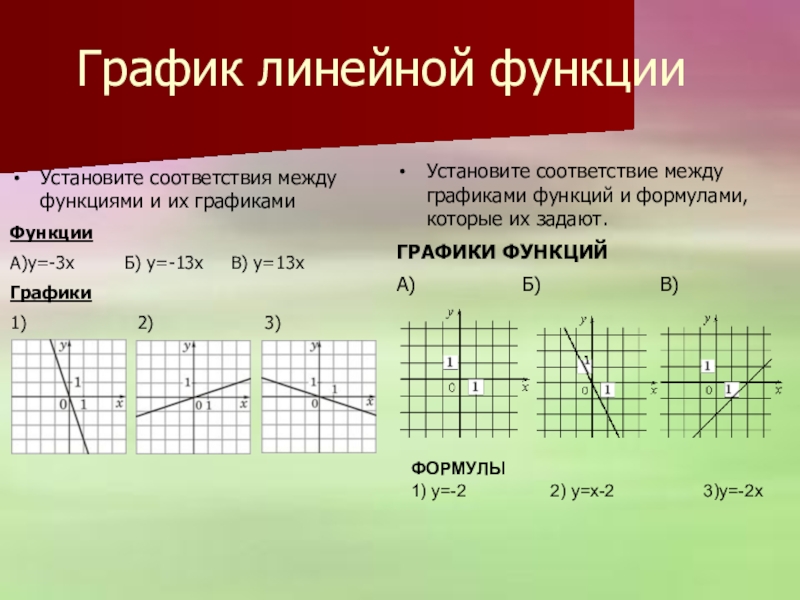
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ ФУНКЦИЙ
А) Б) В)
ФОРМУЛЫ
1) y=-2 2) y=x-2 3)y=-2x
График линейной функции
Слайд 18Особенности расположения графика линейной функции
Если k>0 ,функция возрастает
если K
если b>0,график пересекает ось OY выше 0
если b<0,график пересекает ось OY ниже 0
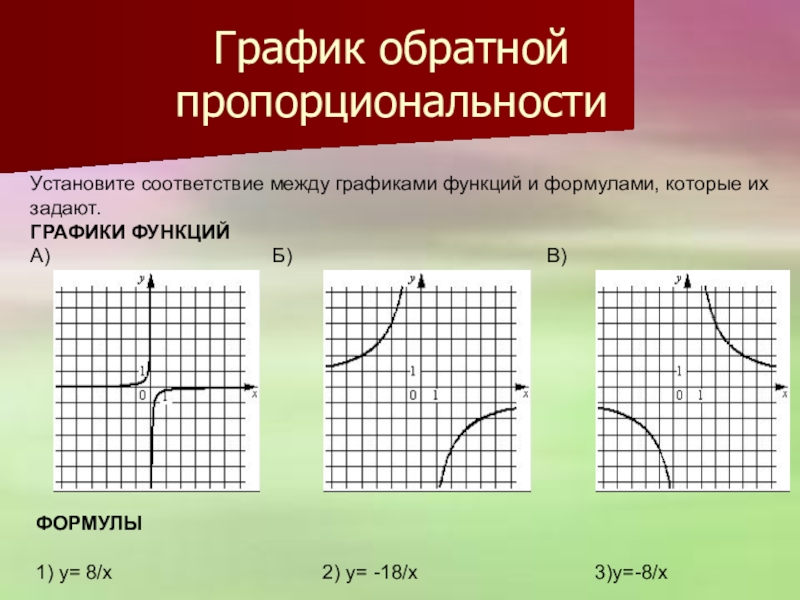
Слайд 19График обратной пропорциональности
Установите соответствие между графиками функций и формулами, которые
ГРАФИКИ ФУНКЦИЙ
А) Б) В)
ФОРМУЛЫ
1) y= 8/x 2) y= -18/x 3)y=-8/x
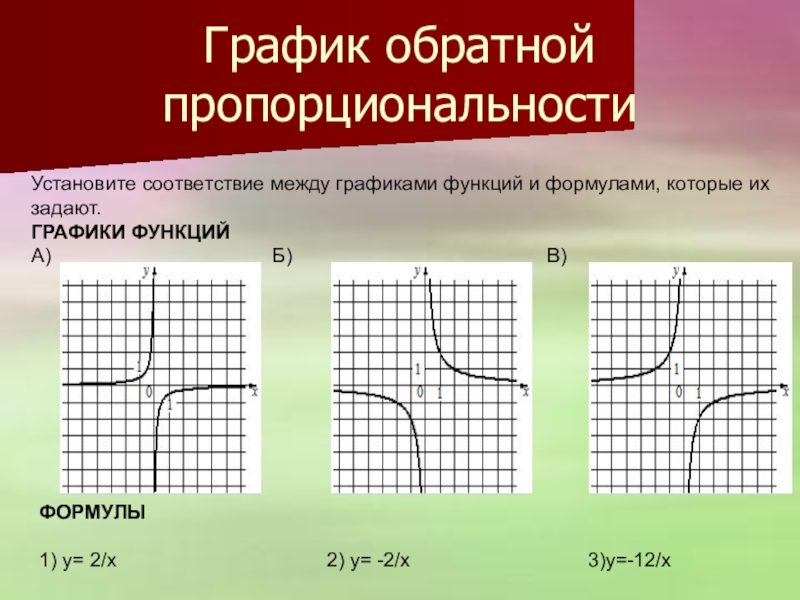
Слайд 20График обратной пропорциональности
Установите соответствие между графиками функций и формулами, которые
ГРАФИКИ ФУНКЦИЙ
А) Б) В)
ФОРМУЛЫ
1) y= 2/x 2) y= -2/x 3)y=-12/x
Слайд 21Особенности расположения графика функции обратной пропорциональности
Если k>0 ,график функции расположен в
Если K<0,график функции расположен во 2 и 4 четверти
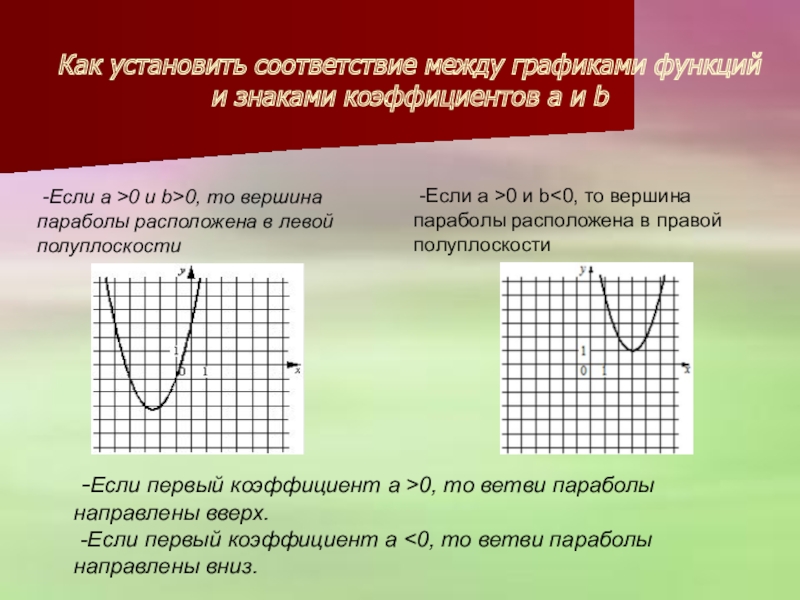
Слайд 22Как установить соответствие между графиками функций и знаками коэффициентов а и
-Если первый коэффициент а >0, то ветви параболы направлены вверх.
-Если первый коэффициент а <0, то ветви параболы направлены вниз.
-Если а >0 и b<0, то вершина параболы расположена в правой полуплоскости
-Если а >0 и b>0, то вершина параболы расположена в левой полуплоскости
Слайд 23
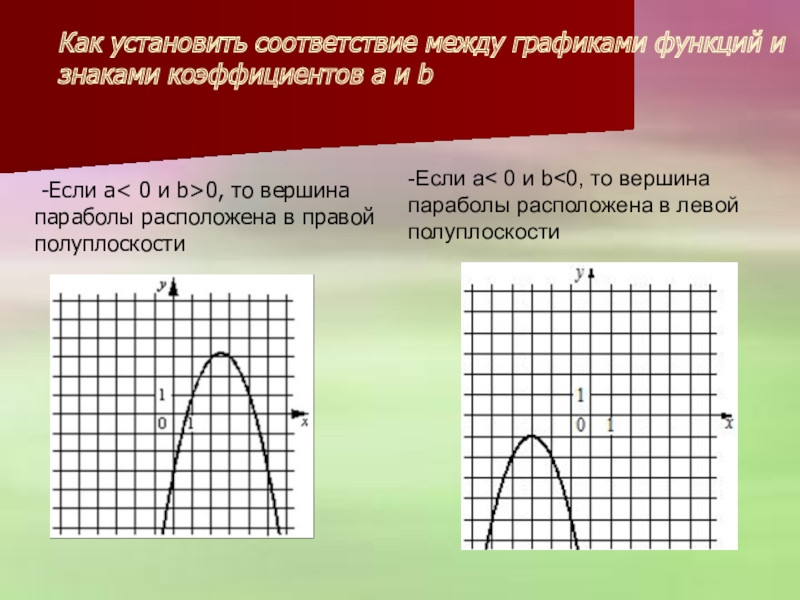
-Если а< 0 и b>0, то вершина параболы расположена в
Как установить соответствие между графиками функций и знаками коэффициентов а и b
-Если а< 0 и b<0, то вершина параболы расположена в левой полуплоскости
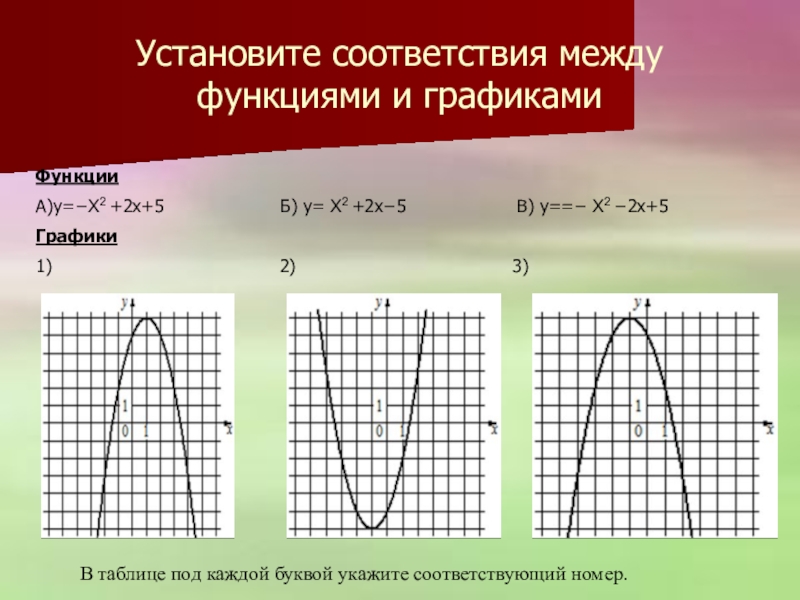
Слайд 24Установите соответствия между функциями и графиками
Функции
А)y=−X2 +2x+5
Графики
1) 2) 3)
В таблице под каждой буквой укажите соответствующий номер.
Слайд 25Нахождение значения коэффициента а по графику квадратичной функции
1) по графику
2) по графику определяем координаты любой точки А (х1;у1)
3) подставляем эти значения в формулу квадратичной функции, заданной в виде:
У=a(х-m)2+n
4) решаем полученное уравнение.
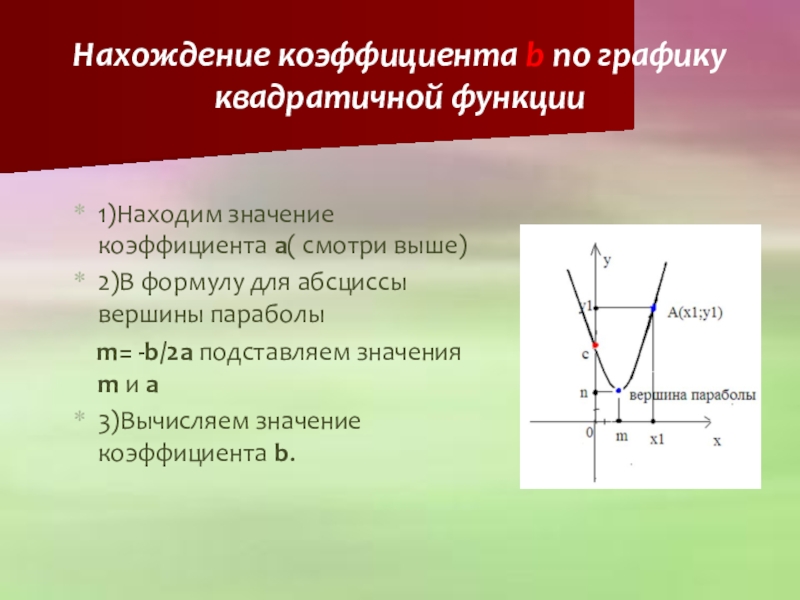
Слайд 26Нахождение коэффициента b по графику квадратичной функции
1)Находим значение коэффициента a( смотри
2)В формулу для абсциссы вершины параболы
m= -b/2a подставляем значения m и a
3)Вычисляем значение коэффициента b.
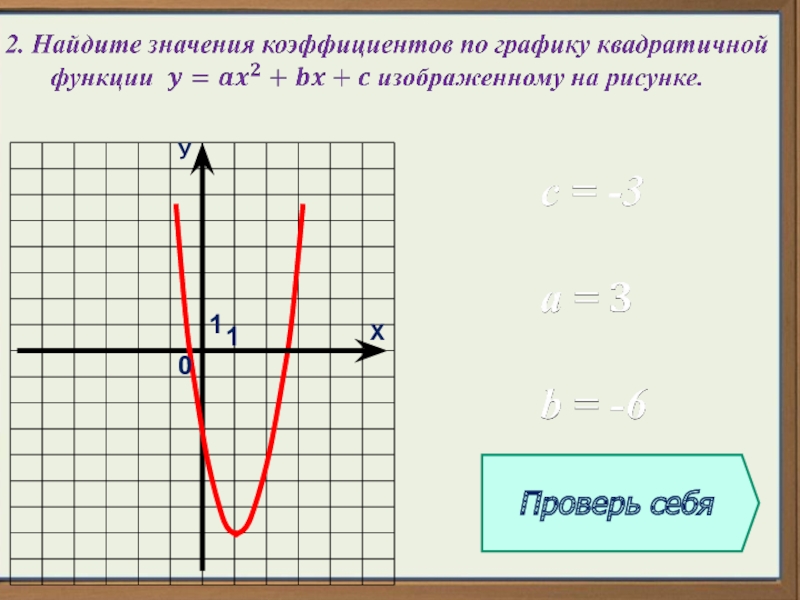
Слайд 27 Нахождение коэффициента с по графику квадратичной функции
1)Находим ординату точки пересечения
Если по графику невозможно найти точку пересечения с осью Оу, то находим коэффициенты a;b
2)Подставляем найденные значения a, b , координаты А(х1 ;у1) в уравнение
у=ax2 +bx+c и находим с.