- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Геометрический смысл производной
Содержание
- 1. Презентация по алгебре на тему Геометрический смысл производной
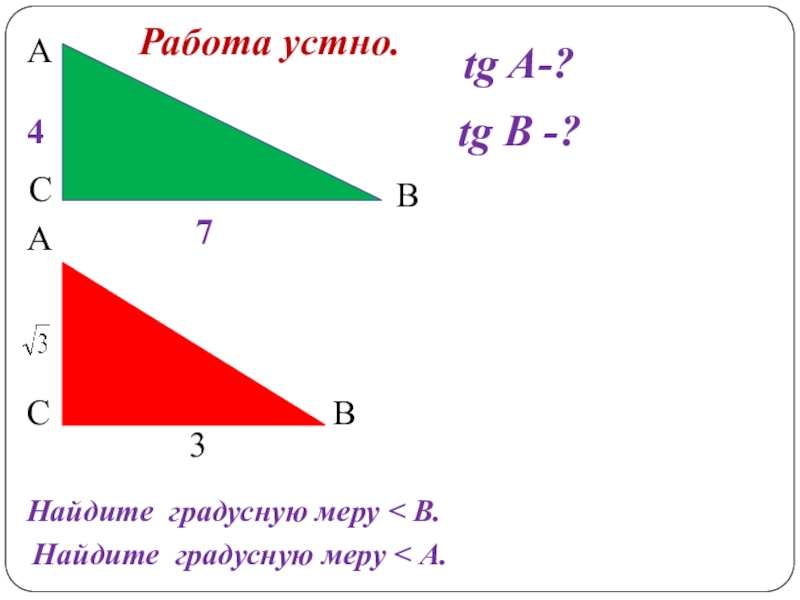
- 2. АСВtg A-?tg В -?47АВСНайдите градусную меру < В.3Найдите градусную меру < А.Работа устно.
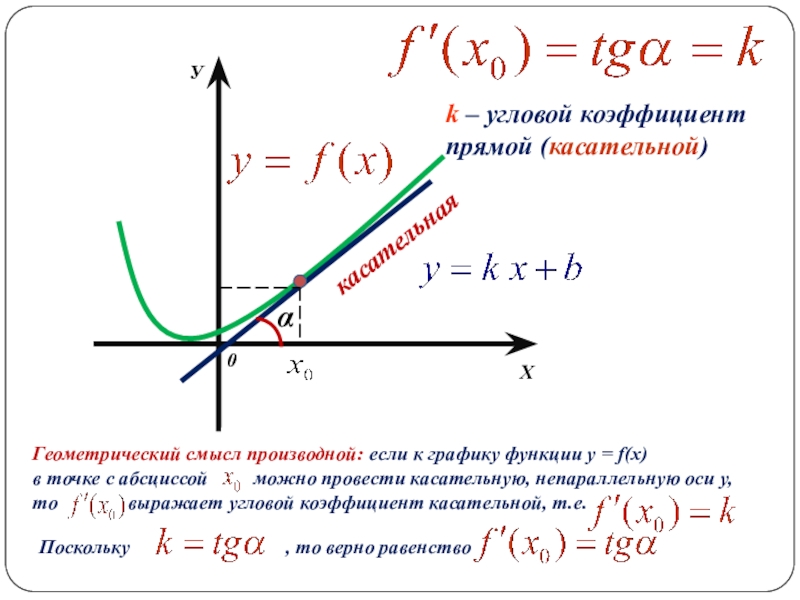
- 3. ХУ0касательнаяαk – угловой коэффициент прямой (касательной)Геометрический смысл
- 4. Слайд 4
- 5. ВНИМАНИЕ!На рисунке изображен график функции
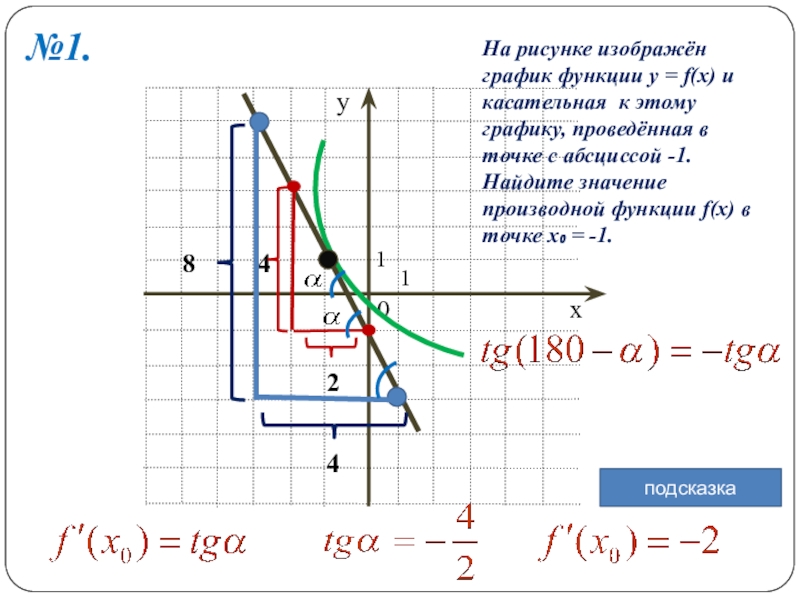
- 6. 10142№1.На рисунке изображён график функции y =
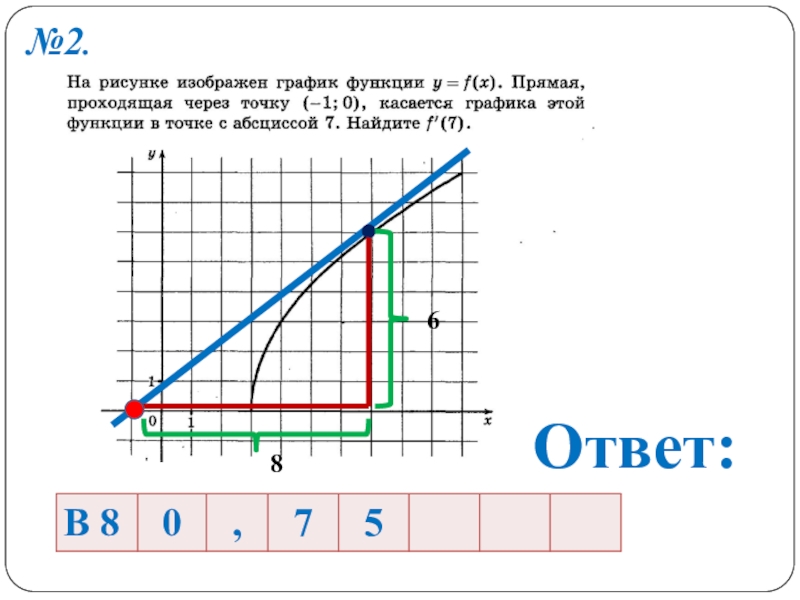
- 7. №2.Ответ:68
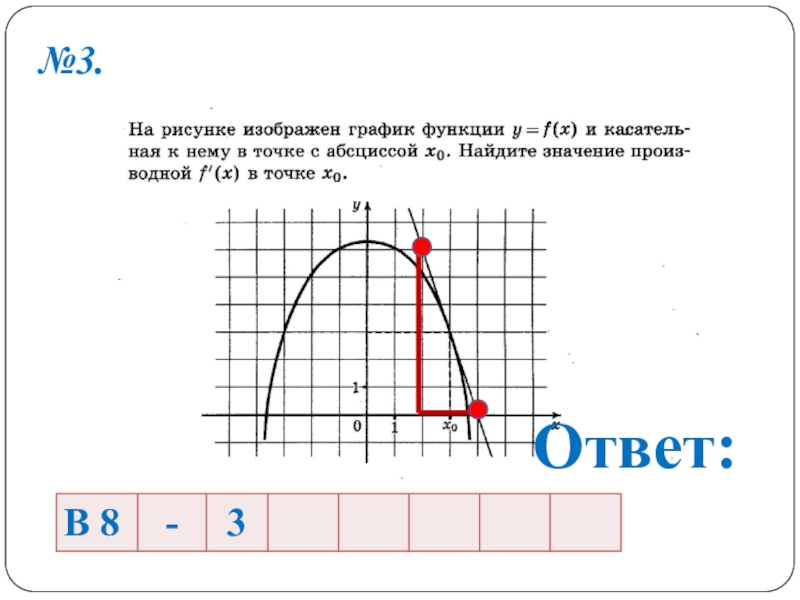
- 8. №3.Ответ:
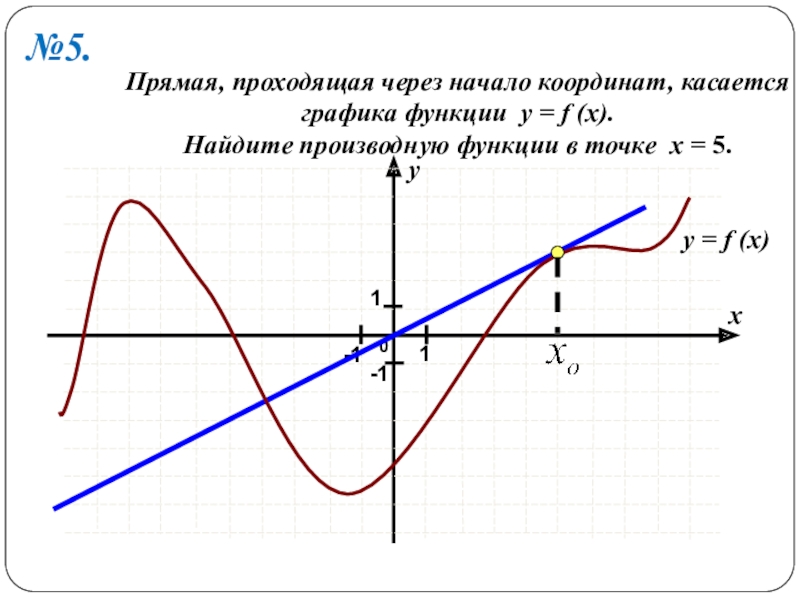
- 9. Прямая, проходящая через начало координат, касаетсяграфика функции
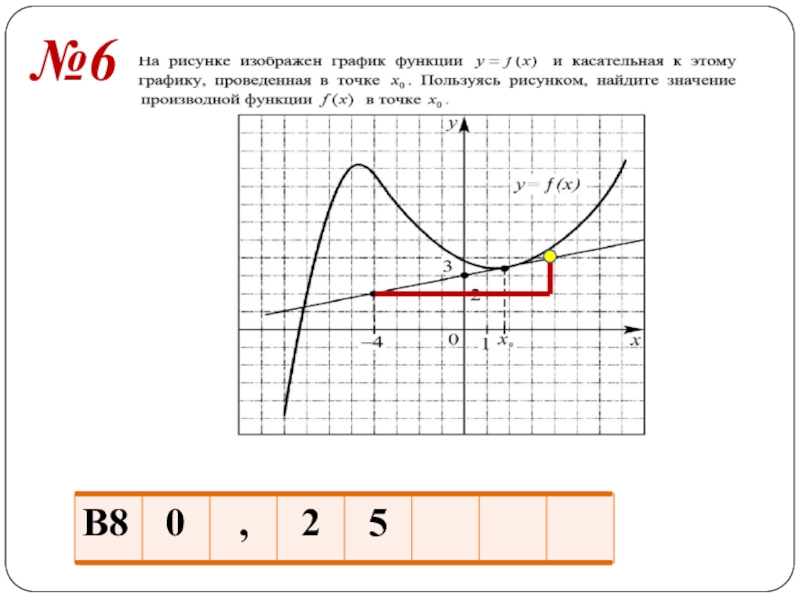
- 10. №6
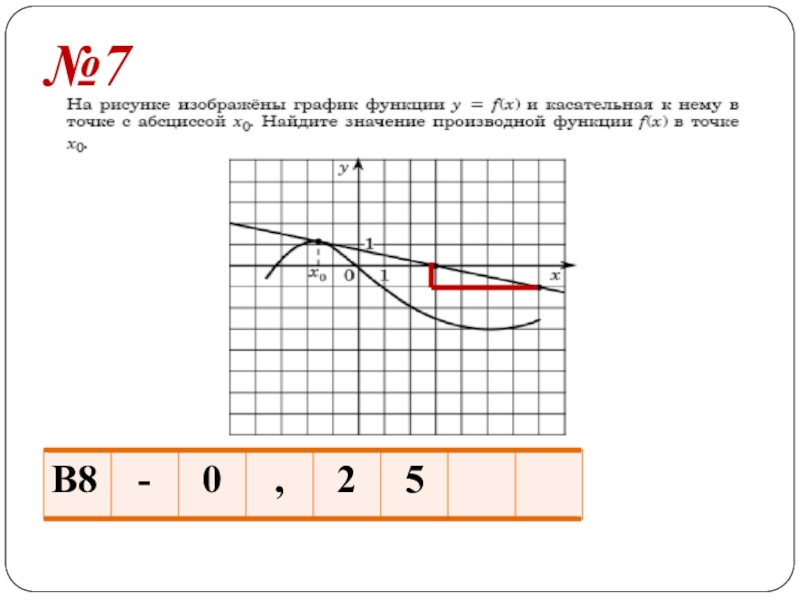
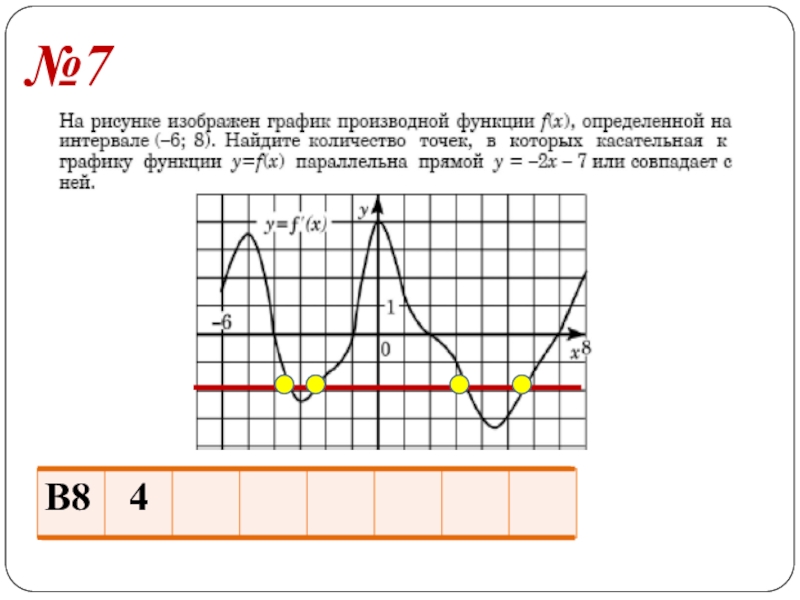
- 11. №7
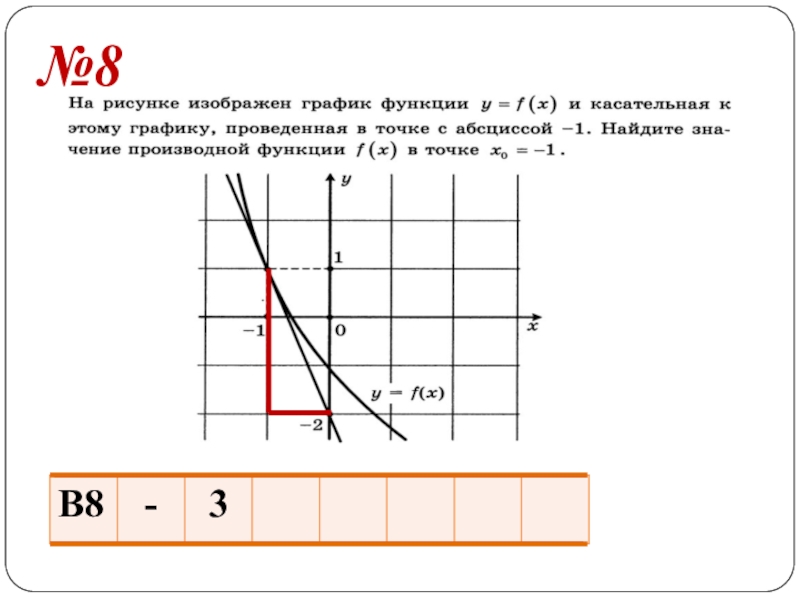
- 12. №8
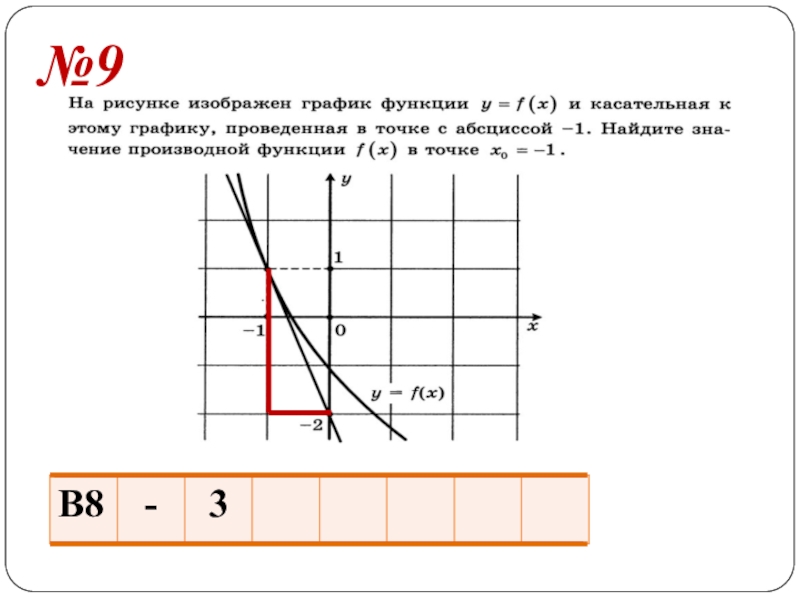
- 13. №9
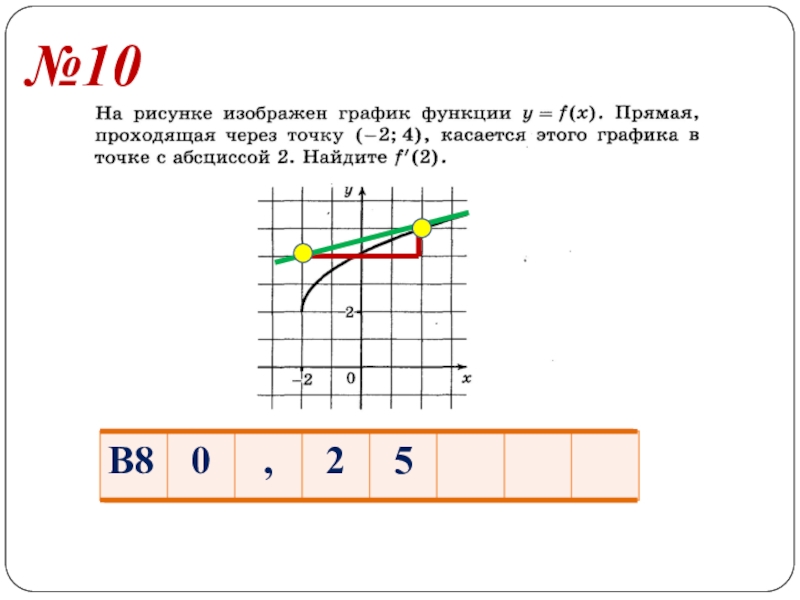
- 14. №10
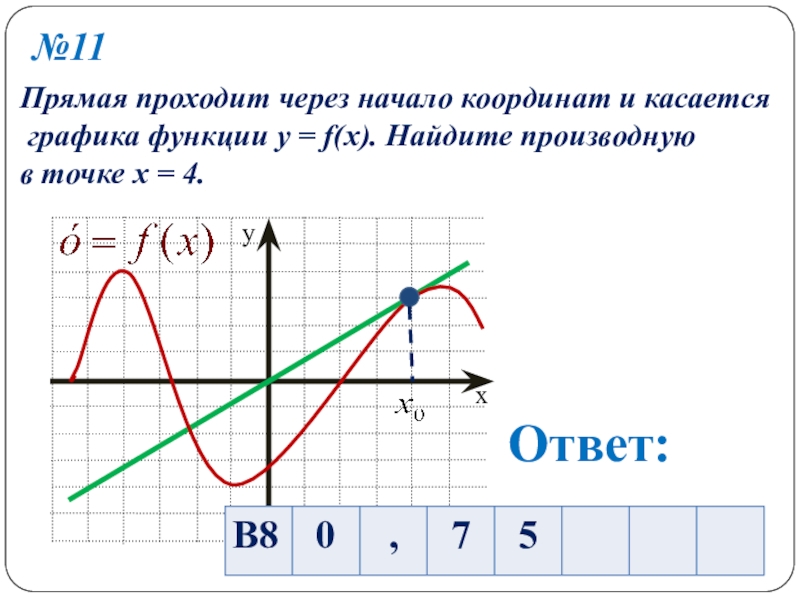
- 15. №11Прямая проходит через начало координат и касается
- 16. ВНИМАНИЕ!На рисунке изображен график производной
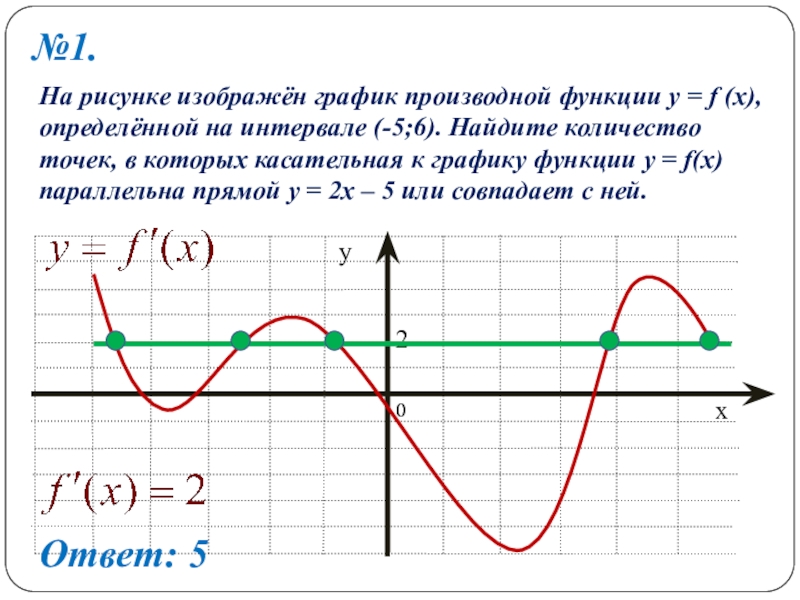
- 17. №1.На рисунке изображён график производной функции y
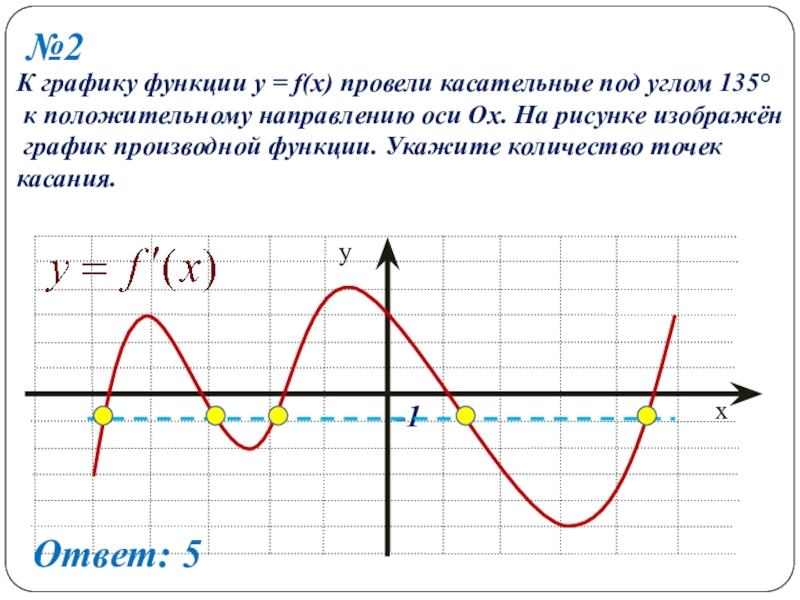
- 18. №2К графику функции y = f(x) провели
- 19. №30113К графику функции y = f(x)проведена касательная
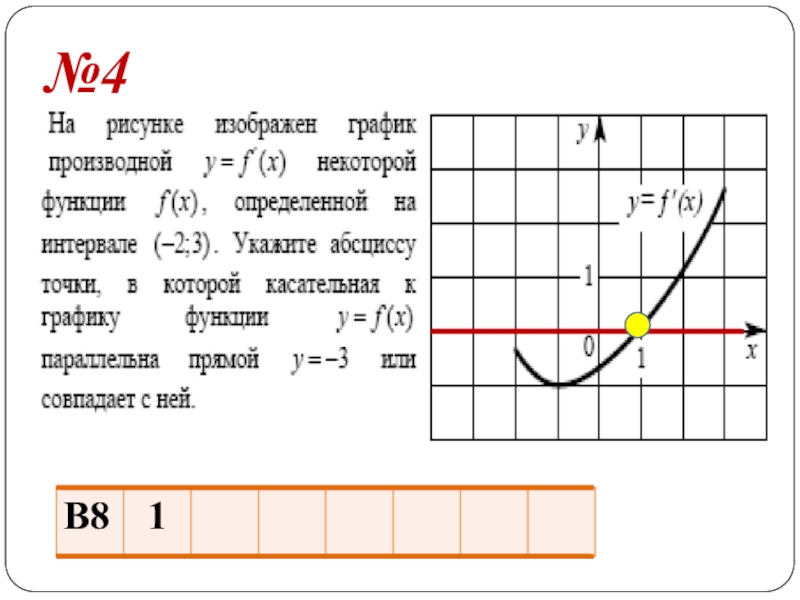
- 20. №4
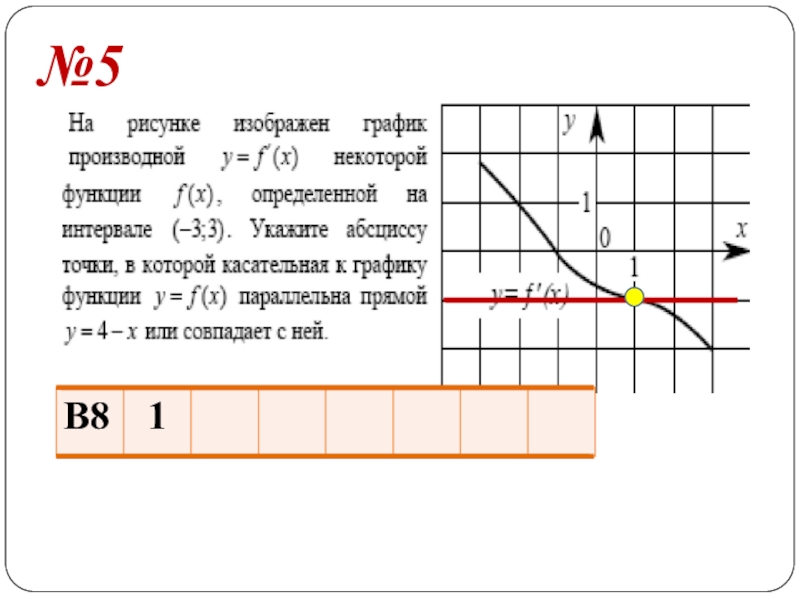
- 21. №5
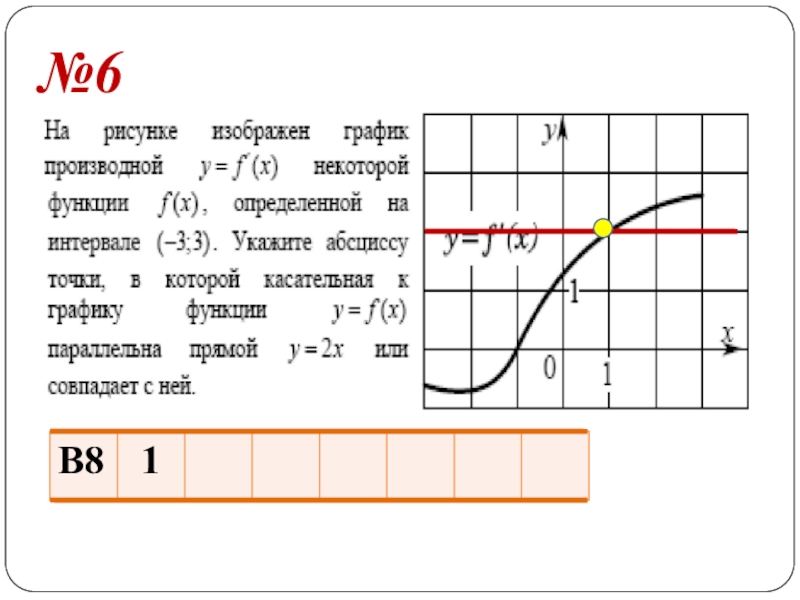
- 22. №6
- 23. №7
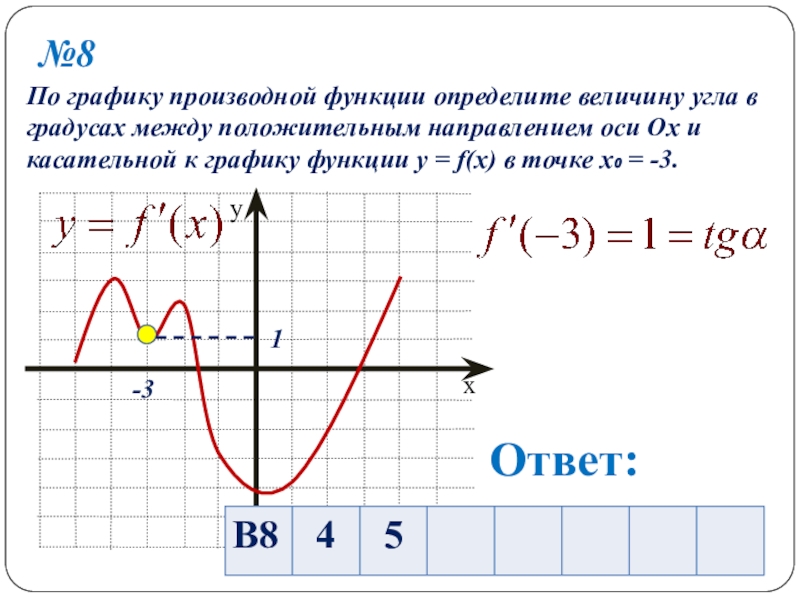
- 24. №8По графику производной функции определите величину угла
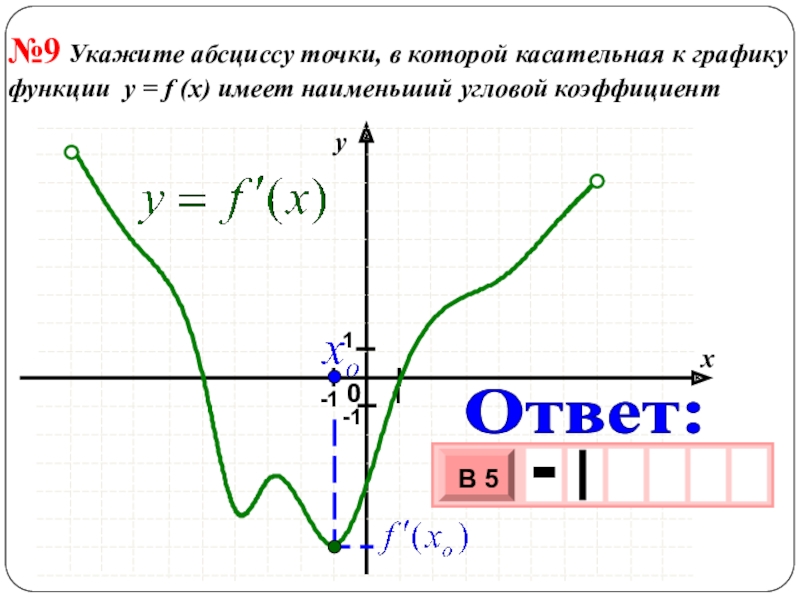
- 25. №9 Укажите абсциссу точки, в которой касательная
АСВtg A-?tg В -?47АВСНайдите градусную меру < В.3Найдите градусную меру < А.Работа устно.
Слайд 3Х
У
0
касательная
α
k – угловой коэффициент прямой (касательной)
Геометрический смысл производной: если к графику
функции y = f(x)
в точке с абсциссой можно провести касательную, непараллельную оси у,
то выражает угловой коэффициент касательной, т.е.
в точке с абсциссой можно провести касательную, непараллельную оси у,
то выражает угловой коэффициент касательной, т.е.
Поскольку , то верно равенство
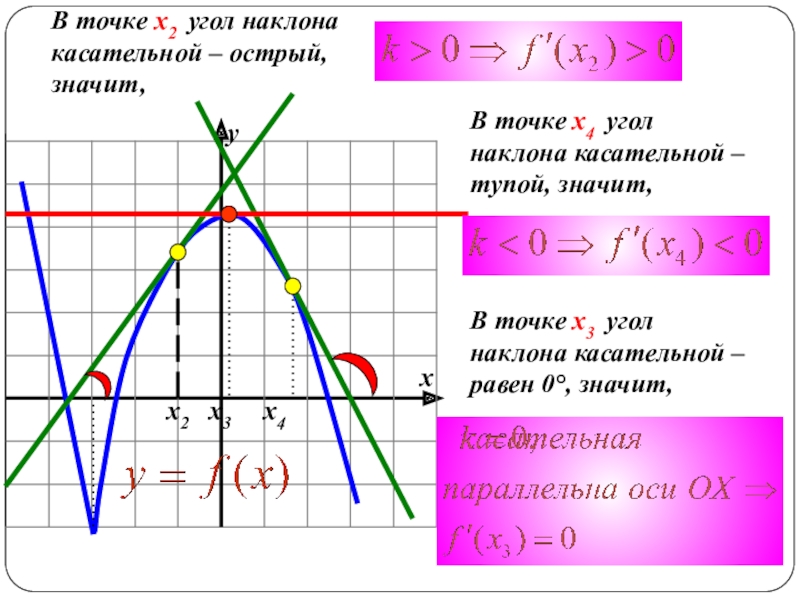
Слайд 4 х2 х3
х4
х
у
В точке х2 угол наклона касательной – острый, значит,
В точке х4 угол наклона касательной – тупой, значит,
В точке х3 угол наклона касательной – равен 0°, значит,
Слайд 61
0
1
4
2
№1.
На рисунке изображён график функции y = f(x) и
касательная к
этому графику, проведённая в точке с абсциссой -1. Найдите значение производной функции f(x) в точке х₀ = -1.
подсказка
4
8
Слайд 9Прямая, проходящая через начало координат, касается
графика функции y = f (x).
Найдите
производную функции в точке х = 5.
y = f (x)
№5.
Слайд 15№11
Прямая проходит через начало координат и касается
графика функции y =
f(x). Найдите производную
в точке х = 4.
в точке х = 4.
Ответ:
Слайд 17№1.
На рисунке изображён график производной функции y = f (x), определённой
на интервале (-5;6). Найдите количество точек, в которых касательная к графику функции y = f(x) параллельна прямой у = 2х – 5 или совпадает с ней.
2
Ответ: 5
0
Слайд 18№2
К графику функции y = f(x) провели касательные под углом 135°
к положительному направлению оси Ох. На рисунке изображён
график производной функции. Укажите количество точек
касания.
график производной функции. Укажите количество точек
касания.
-1
Ответ: 5
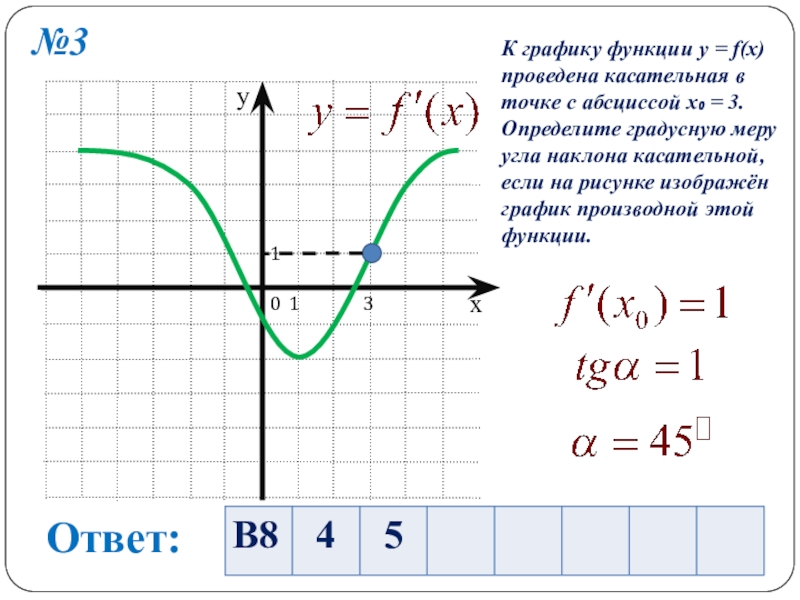
Слайд 19№3
0
1
1
3
К графику функции y = f(x)
проведена касательная в
точке с абсциссой
х₀ = 3.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
Ответ:
Слайд 24№8
По графику производной функции определите величину угла в градусах между положительным
направлением оси Ох и касательной к графику функции y = f(x) в точке х₀ = -3.
-3
1
Ответ:
Слайд 25№9 Укажите абсциссу точки, в которой касательная к графику
функции y =
f (x) имеет наименьший угловой коэффициент
