понимании
и искусном применении всего того,
что знаешь.
Георг Гегель
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Геометрическая прорессия (9 класс)
Содержание
- 1. Презентация по алгебре на тему Геометрическая прорессия (9 класс)
- 2. Вспомни!Что такое геометрическая прогрессия?Числовая последовательность, первый
- 3. Как называется число, которое надо умножить предыдущий член, чтобы получить последующий?Знаменатель геометрической прогрессии
- 4. Назовите формулу n- го члена геометрической прогрессии? bn=b1qn-1
- 5. В благоприятных условиях бактерии размножаются так,
- 6. Формула для вычисления значения суммы n первых членовгеометрической прогрессии
- 7. Цель урока: Формирование понятия суммы n-первых членов
- 8. Ожидаемые результаты:знать: формулу для вычисления значения суммы
- 9. Слайд 9
- 10. Пример: Найдем сумму 1+3+32+33+34+35+36+37Данная сумма
- 11. S8 =Ответ: 3280Решение:
- 12. Вычисли: Сумму пяти первых членов, заданных геометрических
- 13. Сумму первых десяти членов геометрической прогрессии: 10; 20; 40;….НайдиОтвет: 10230
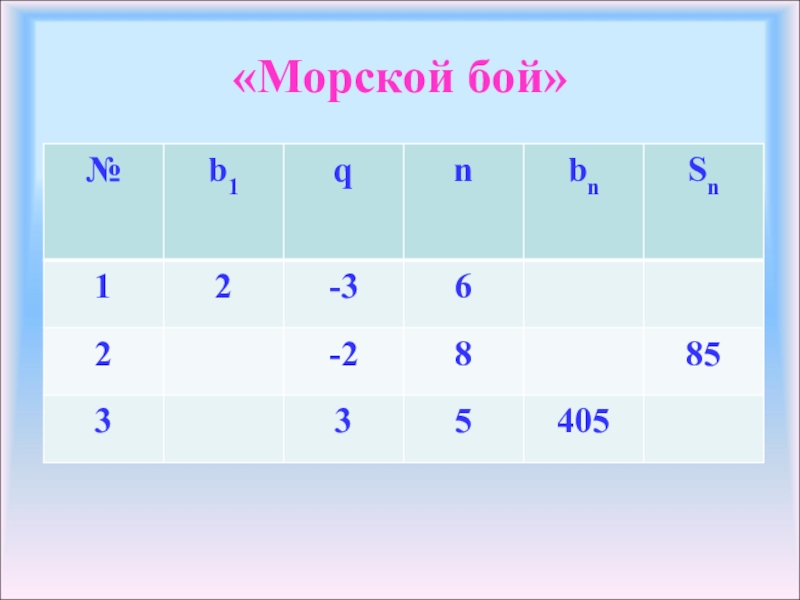
- 14. «Морской бой»
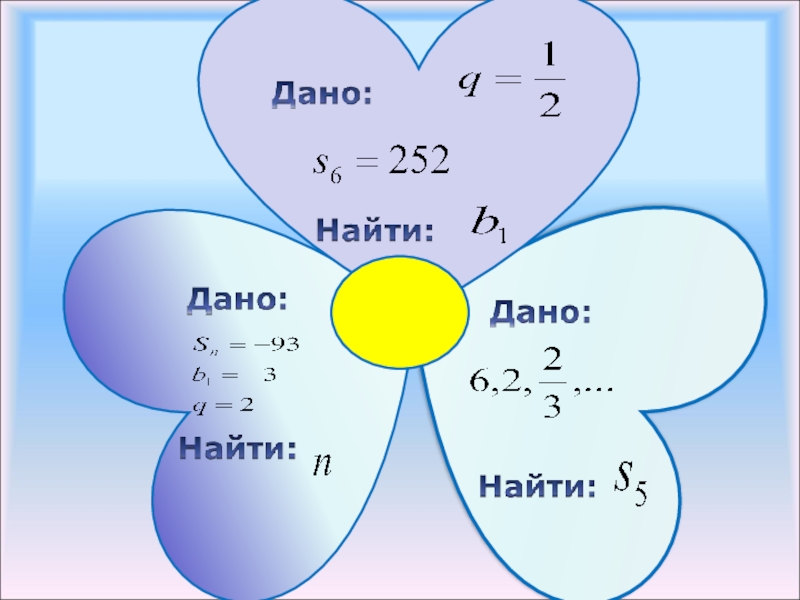
- 15. Слайд 15
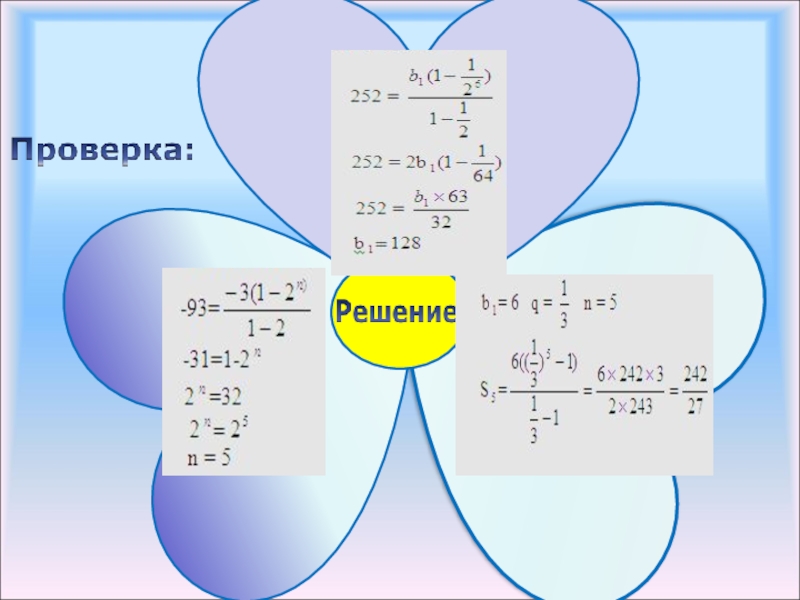
- 16. Слайд 16
- 17. РешиДано: 5; 10; 20…- геометрическая прогрессия. Найдите S7.Ответ: 635
Вспомни!Что такое геометрическая прогрессия?Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же, не равное нулю, число, называется геометрической прогрессией.
Слайд 2 Вспомни!
Что такое геометрическая прогрессия?
Числовая последовательность, первый член которой отличен от
нуля, а каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же, не равное нулю, число, называется геометрической прогрессией.
Слайд 3Как называется число, которое надо умножить предыдущий член, чтобы получить последующий?
Знаменатель
геометрической прогрессии
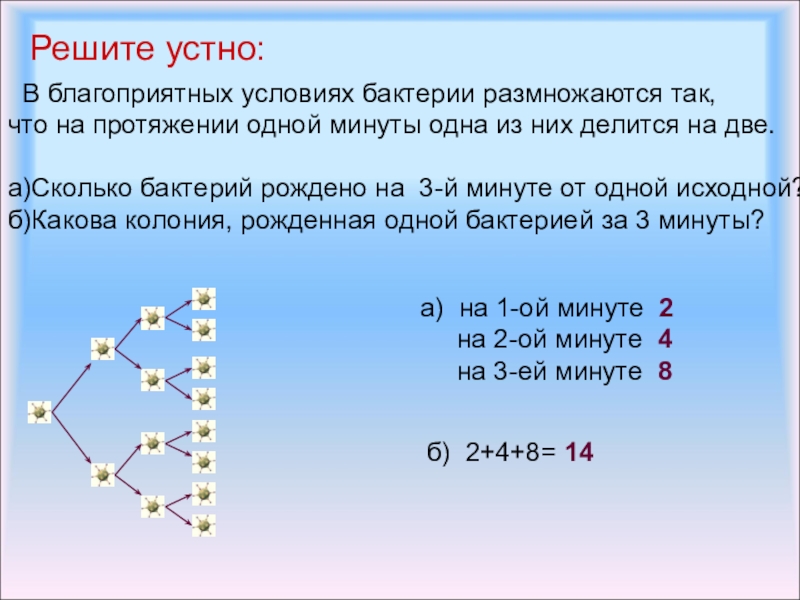
Слайд 5 В благоприятных условиях бактерии размножаются так,
что на протяжении одной
минуты одна из них делится на две.
а)Сколько бактерий рождено на 3-й минуте от одной исходной?
б)Какова колония, рожденная одной бактерией за 3 минуты?
а)Сколько бактерий рождено на 3-й минуте от одной исходной?
б)Какова колония, рожденная одной бактерией за 3 минуты?
а) на 1-ой минуте 2
на 2-ой минуте 4
на 3-ей минуте 8
б) 2+4+8= 14
Решите устно:
Слайд 7Цель урока:
Формирование понятия суммы n-первых членов геометрической прогрессии. Вывод формулы
суммы n-первых членов геометрической прогрессии. Отработка навыков применения формулы суммы суммы n-первых членов геометрической прогрессии.
Слайд 8Ожидаемые результаты:
знать: формулу для вычисления значения суммы n-первых членов геометрической прогрессии;
уметь:
вычислять значение суммы n-первых членов геометрической прогрессии.
Слайд 10 Пример: Найдем сумму 1+3+32+33+34+35+36+37
Данная сумма является суммой первых восьми
членов геометрической прогрессии, в которой b1=1, q=3
Слайд 12Вычисли:
Сумму пяти первых членов, заданных геометрических прогрессий:
4; 12; 36;…..
20;
10; 5;…..
Ответ: 1) -484
2) 38,75