- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Функция, определение функции, чётные и нечётные функции, построение графиков
Содержание
- 1. Презентация по алгебре на тему Функция, определение функции, чётные и нечётные функции, построение графиков
- 2. В работе И. Барроу (“Лекции
- 3. С начала ХIХ века
- 4. Сам термин “функция” впервые появляется только в
- 5. Современное определение Функции, отлича-ющееся от упоминаний
- 6. 1. Что называется числовой функцией?2. Объясните, что
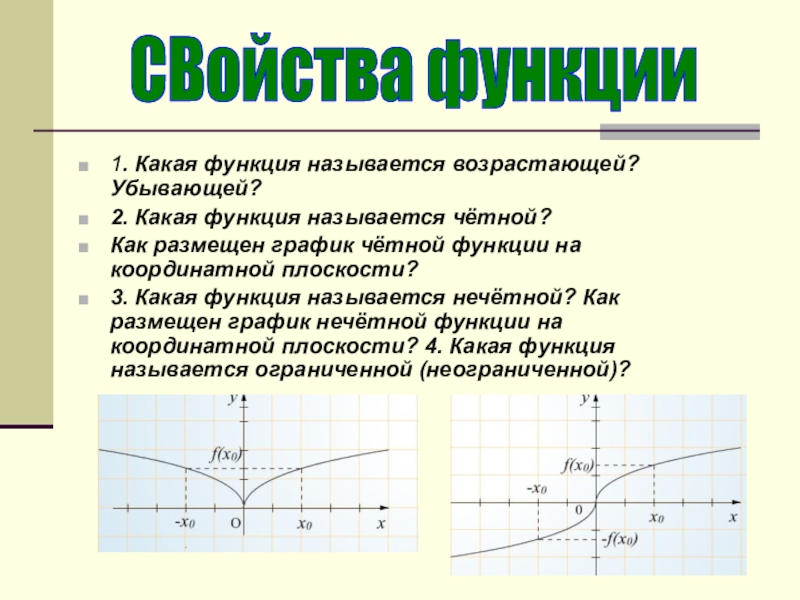
- 7. 1. Какая функция называется возрастающей? Убывающей? 2.
- 8. Определить по графикам данных функций их основные свойстваИсследование
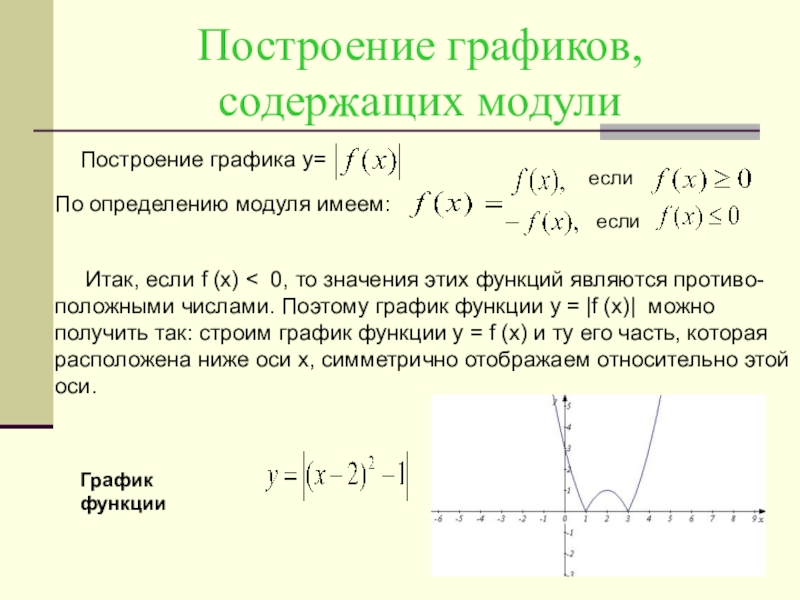
- 9. Построение графиков, содержащих модулиПостроение графика у=По определению
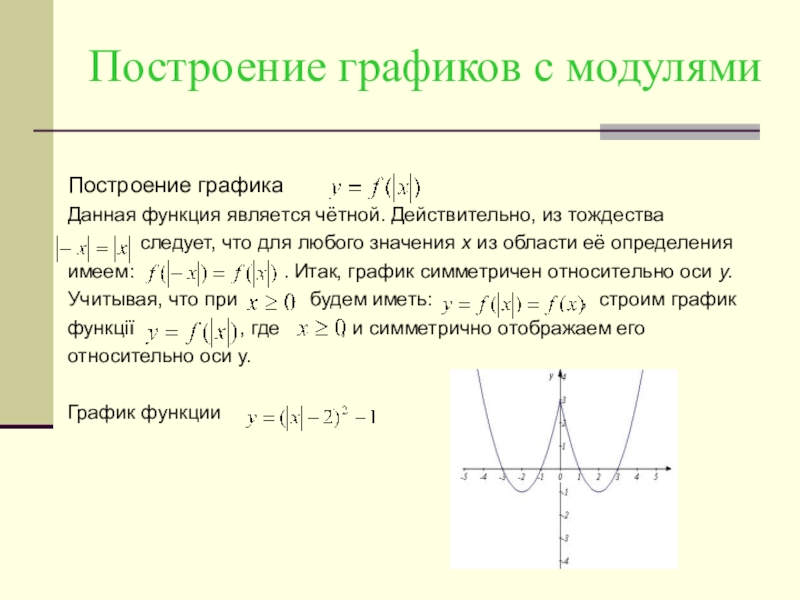
- 10. Построение графиков с модулямиПостроение графикаДанная функция является
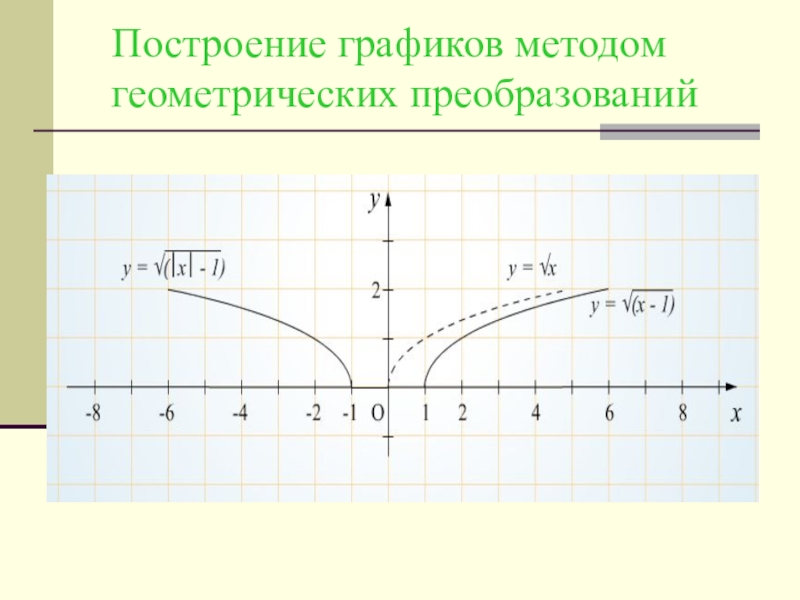
- 11. Построение графиков методом геометрических преобразований
- 12. Выполни самостоятельноКакие преобразования необходимо выполнить для построения графиков функций?
- 13. Чётные и нечётные функции Определение. Функцию f
- 14. Чётные и нечётные функции Выполнение равенства f
- 15. Пример 1Докажите, что функцияf (x) = x3
- 16. Пример 21. Исследовать функцию на чётностьf(х)=Решение. Имеем:
- 17. Правила нахождения максимума и минимума функцииах
- 18. Правило 2. Нахождение максимума и минимума
- 19. Нахождение наибольшего и наименьшего значения функцииасdbФункция y=f
- 20. Общая схема исследования функции и построение
- 21. Построить графики функций1. у =2. у =3. у =4. у = 25. у =
- 22. Самостоятельная работаВариант №11. Найти область определения функции
- 23. Домашняя работаПостройте графики функций:
Слайд 2
В работе И. Барроу (“Лекции по геометрии”,1670 г.)
В геометрическом и механическом виде это понятие мы находим и у И. Ньютона.
Путь развития понятия функции
Слайд 3
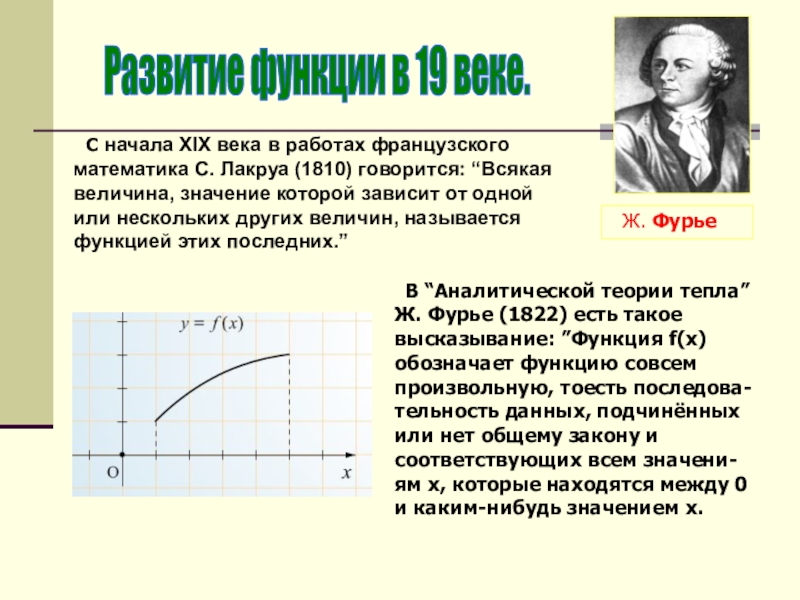
С начала ХIХ века в работах французского математика
В “Аналитической теории тепла” Ж. Фурье (1822) есть такое высказывание: ”Функция f(x) обозначает функцию совсем произвольную, тоесть последова-тельность данных, подчинённых или нет общему закону и соответствующих всем значени-ям х, которые находятся между 0 и каким-нибудь значением х.
Ж. Фурье
Развитие функции в 19 веке.
Слайд 4
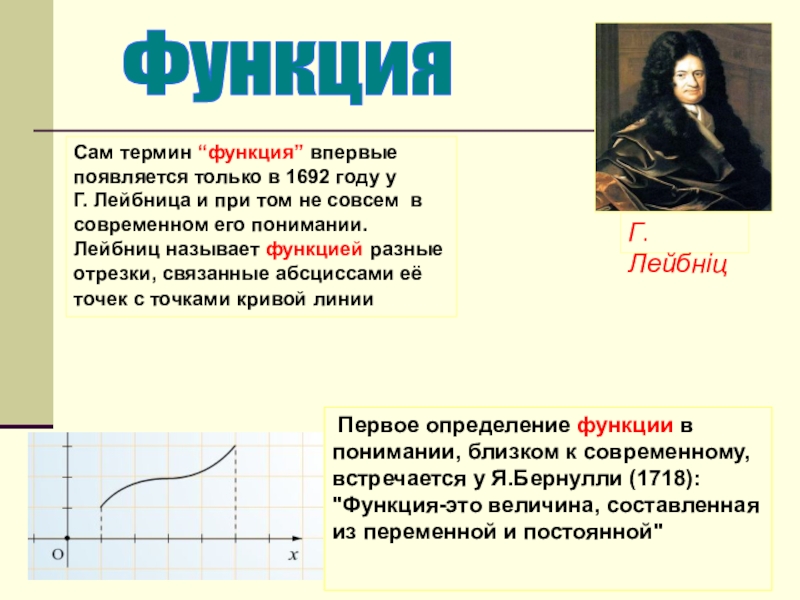
Сам термин “функция” впервые появляется только в 1692 году у
Г. Лейбница
Г. Лейбніц
Первое определение функции в понимании, близком к современному, встречается у Я.Бернулли (1718): "Функция-это величина, составленная из переменной и постоянной"
Функция
Слайд 5 Современное определение Функции, отлича-ющееся от упоминаний об аналитическом задании, которое
Современное определение Функции
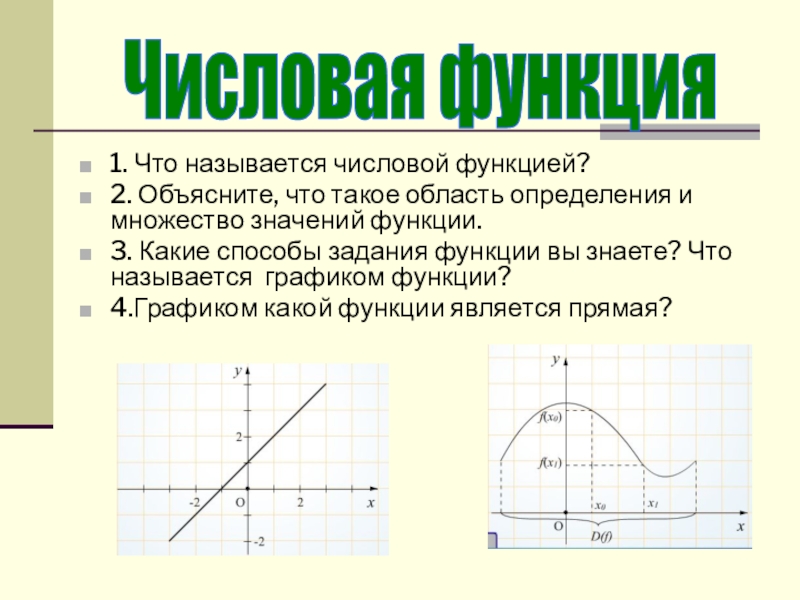
Слайд 61. Что называется числовой функцией?
2. Объясните, что такое область определения и
3. Какие способы задания функции вы знаете? Что называется графиком функции?
4.Графиком какой функции является прямая?
Числовая функция
Слайд 71. Какая функция называется возрастающей? Убывающей?
2. Какая функция называется чётной?
Как размещен график чётной функции на координатной плоскости?
3. Какая функция называется нечётной? Как размещен график нечётной функции на координатной плоскости? 4. Какая функция называется ограниченной (неограниченной)?
СВойства функции
Слайд 9Построение графиков, содержащих модули
Построение графика у=
По определению модуля имеем:
График функции
если
если
Слайд 10Построение графиков с модулями
Построение графика
Данная функция является чётной. Действительно, из тождества
следует, что для любого значения x из области её определения
имеем: . Итак, график симметричен относительно оси у.
Учитывая, что при будем иметь: , строим график
функції , где , и симметрично отображаем его
относительно оси у.
График функции
Слайд 12Выполни самостоятельно
Какие преобразования необходимо выполнить для построения графиков функций?
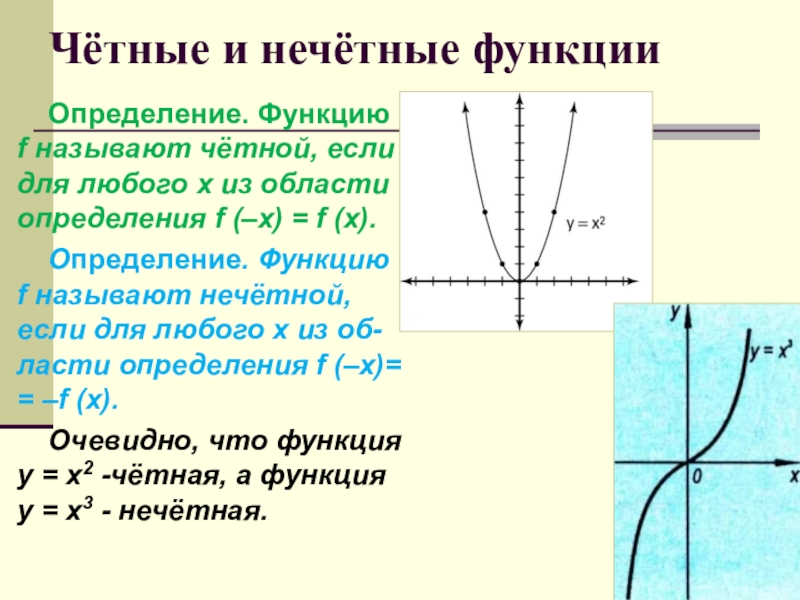
Слайд 13Чётные и нечётные функции
Определение. Функцию f называют чётной, если для
Определение. Функцию f называют нечётной, если для любого x из об-ласти определения f (–x)= = –f (x).
Очевидно, что функция y = x2 -чётная, а функция y = x3 - нечётная.
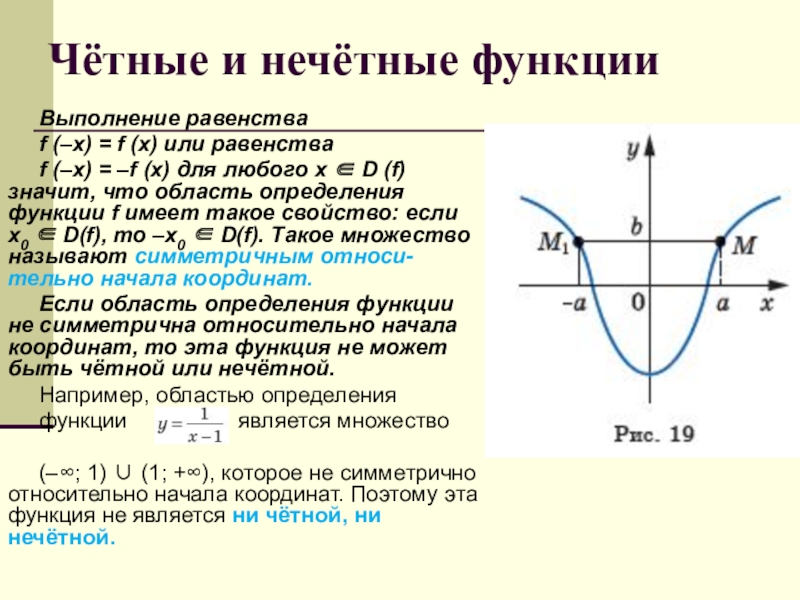
Слайд 14Чётные и нечётные функции
Выполнение равенства
f (–x) = f (x)
f (–x) = –f (x) для любого x ∈ D (f) значит, что область определения функции f имеет такое свойство: если x0 ∈ D(f), то –x0 ∈ D(f). Такое множество называют симметричным относи-тельно начала координат.
Если область определения функции не симметрична относительно начала координат, то эта функция не может быть чётной или нечётной.
Например, областью определения
функции является множество
(–∞; 1) ∪ (1; +∞), которое не симметрично относительно начала координат. Поэтому эта функция не является ни чётной, ни нечётной.
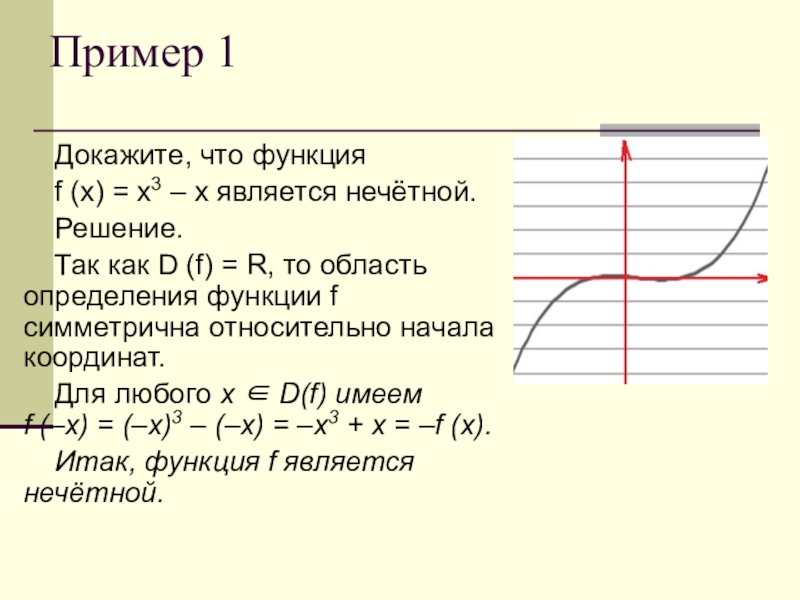
Слайд 15Пример 1
Докажите, что функция
f (x) = x3 – x является нечётной.
Решение.
Так как D (f) = R, то область определения функции f симметрична относительно начала координат.
Для любого x ∈ D(f) имеем f (–x) = (–x)3 – (–x) = –x3 + x = –f (x).
Итак, функция f является нечётной.
Слайд 16Пример 2
1. Исследовать функцию на чётность
f(х)=
Решение. Имеем:
Итак, область определения функции симметрична относительно начала координат. Для любого х D(f) имеем:
f(-х)= = = f(х).
Итак, функция является чётной.
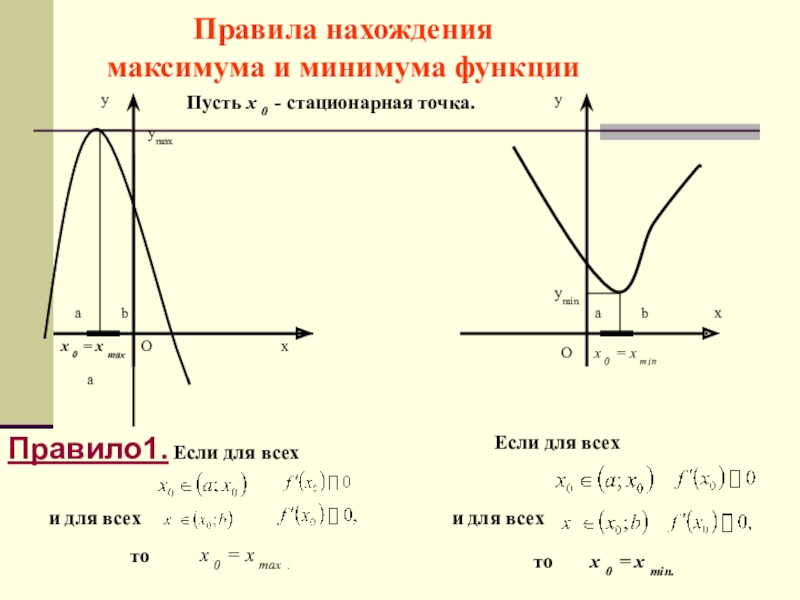
Слайд 17Правила нахождения
максимума и минимума функции
а
х 0 = х max
х 0
ymax
ymin
y
y
x
x
O
O
Пусть x 0 - cтационарная точка.
Правило1. Если для всех
и для всех
то
х 0 = х max .
Если для всех
и для всех
то
х 0 = х min.
a
a
b
b
Слайд 18Правило 2.
Нахождение максимума и минимума функции
1. Если
то
х 0 = х
2. Если
то
х 0 = х min.
Это правило нельзя применять при исследовании на экстремум тех точек, в которых производная первого порядка не существует, а также ко стационарным точкам, в которых производная второго порядка равна нулю. В таких случаях нужно использовать первое правило.
Слайд 19Нахождение наибольшего и наименьшего значения функции
а
с
d
b
Функция y=f (x) непрерывна на [a;
Чтобы найти наибольшее ( наименьшее ) значение функции на отрезке [a; b], нужно:
найти все локальные максимумы (минимумы);
значения функции на концах отрезка;
наибольшее ( наименьшее) число полученного множества и будет наибольшим ( наименьшим ) значением функции на [a; b].
min f (x)=f (a) ; max f (x)=f (c) ;
[ a; b] [ a; b]
Слайд 20Общая схема исследования функции
и построение её графика
Область определения функции D(y).
Нули
Чётность, нечётность, периодичность.
Стационарные точки.
Точки экстремума и промежутки монотонности.
Построение графика.
Слайд 22Самостоятельная работа
Вариант №1
1. Найти область определения функции у =
2. Составить уравнение касательной к кривой у = в точке с абсциссой Х=1 и проиллюстрировать решение.
3. Построить график функции и исследовать её на экстремум.
Вариант №2
1. Найти область определения функции у = .
2. Составить уравнение касательной к кривой в точке с абсциссой Х=1 и проиллюстрировать решение.
3. Построить график функции и исследовать её на экстремум.






![Презентация по алгебре на тему Функция, определение функции, чётные и нечётные функции, построение графиков Нахождение наибольшего и наименьшего значения функцииасdbФункция y=f (x) непрерывна на [a; Нахождение наибольшего и наименьшего значения функцииасdbФункция y=f (x) непрерывна на [a; b].Чтобы найти наибольшее ( наименьшее )](/img/thumbs/931d46950f99feb836701c6f38fdb14f-800x.jpg)









