- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Линейная функция
Содержание
- 1. Презентация по алгебре на тему Линейная функция
- 2. Линейная функция и её график07 05 18Классная работа
- 3. Устная работа1. Даны уравнения. Какие из них
- 4. Устная работа
- 5. Устная работа 3. Укажите, у какой из
- 6. Решение задач Условия оплаты повременной телефонной связи
- 7. Решение задачЕсли тело движется с постоянным ускорением
- 8. Решение задач3. В баке легкового автомобиля 50
- 9. Что общего во всех этих формулах?c =
- 10. x – независимая переменная (аргумент)y – зависимая
- 11. Устные задания в) у = 4х –
- 12. Задание 2. Является ли функция линейной?А) у
- 13. -5-2147Устные заданияЗадание 3. Линейная функция задана формулой
- 14. Через две точки можно провести только одну прямую линию.Для построения графика линейной функции достаточно двух точек!
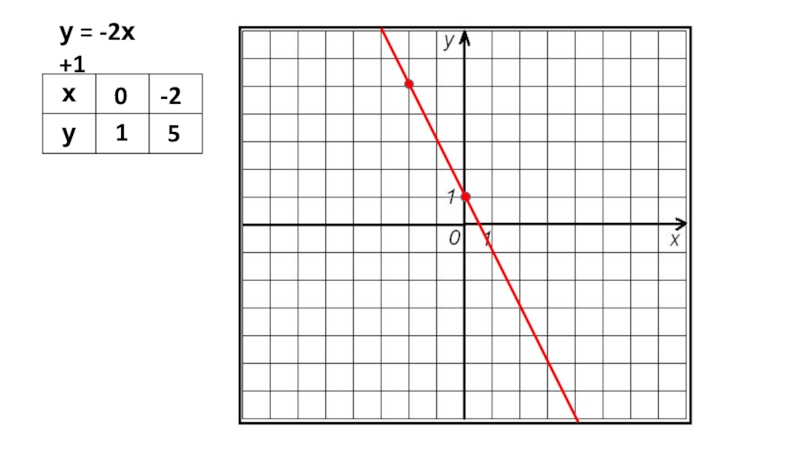
- 15. у = -2х +10-215
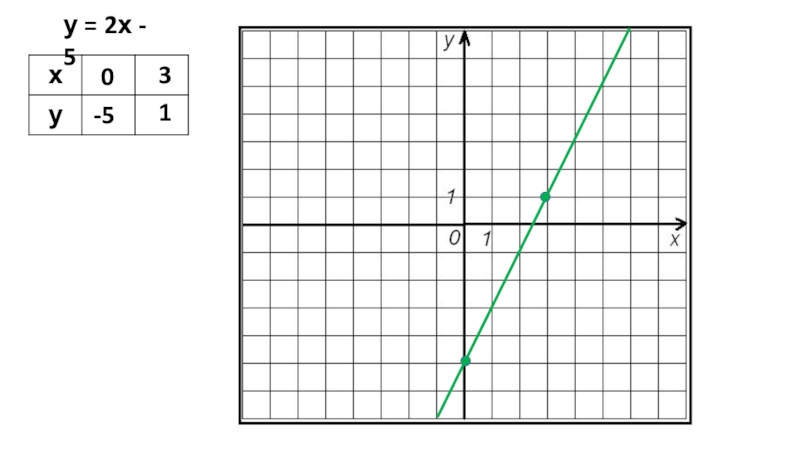
- 16. у = 2х - 503-51
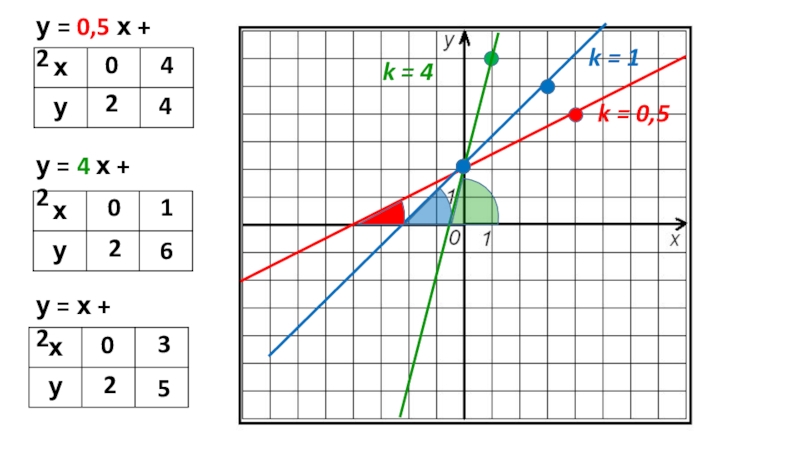
- 17. у = 0,5 х + 2у =
- 18. Чем больше угловой коэффициент k, тем больше угол, образованный графиком функции с осью ОХ
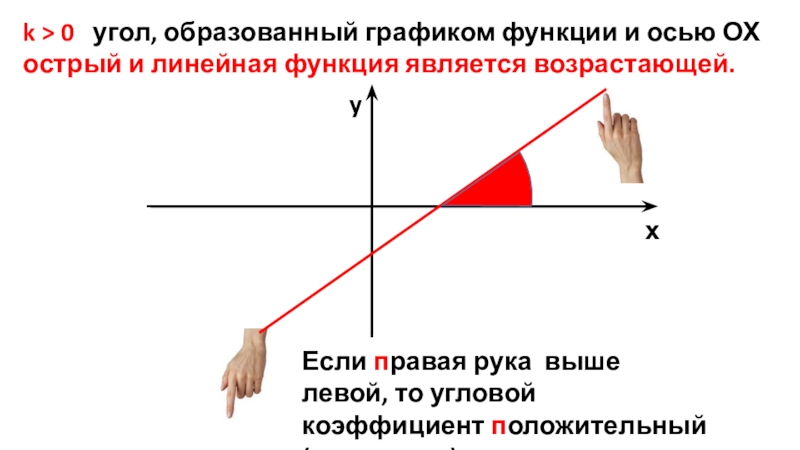
- 19. k > 0 угол, образованный графиком
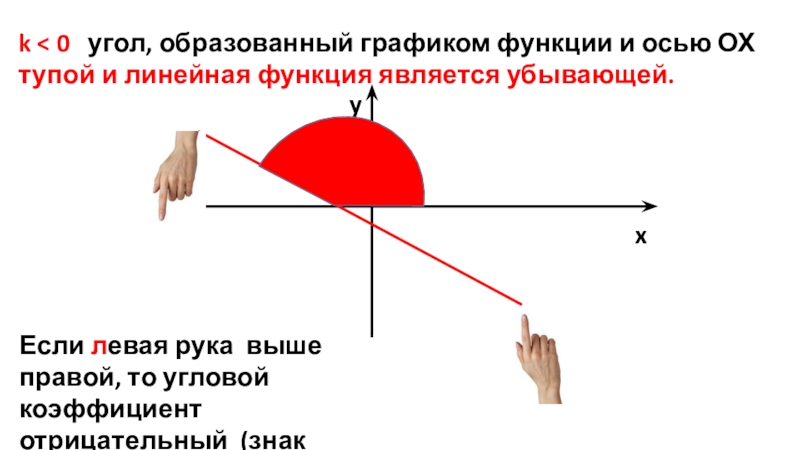
- 20. k < 0 угол, образованный графиком
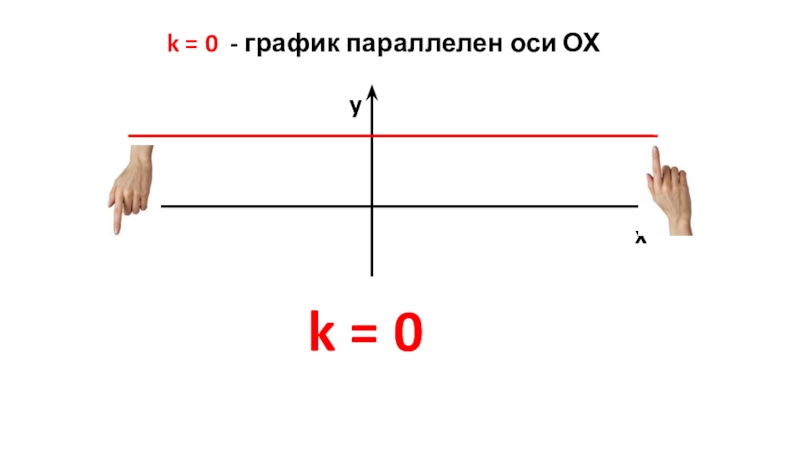
- 21. k = 0 - график параллелен оси ОХxyk = 0
- 22. Построим несколько графиков линейных функций, у которых одинаковые угловые коэффициенты.
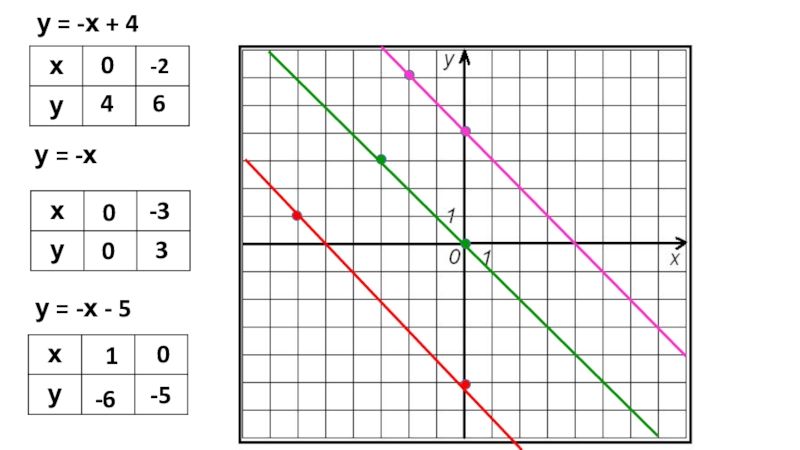
- 23. у = -х + 4у = -х у = -х - 5 04-2600-330-5-61
- 24. Если у линейных функций угловой коэффициент одинаковый, то их графики параллельны!
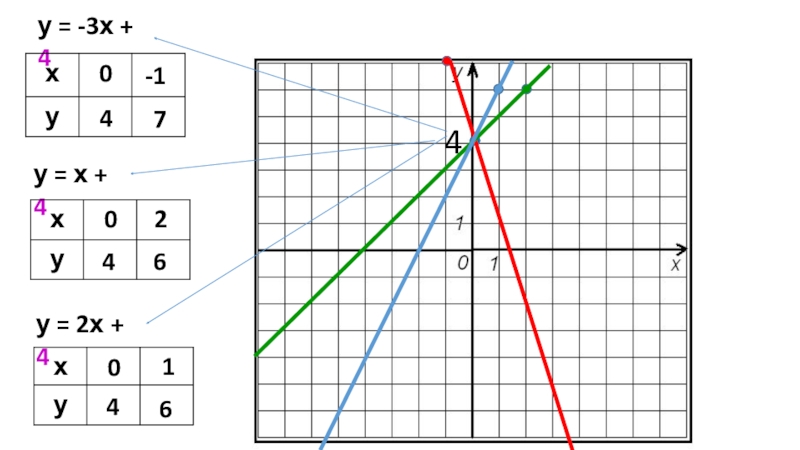
- 25. у = -3х + 4у = х + 4у = 2х + 404-17042604164
- 26. х =0 , y = k
- 27. 1) Роль параметра k.Если k > 0, то линейная функция
- 28. Слайд 28
- 29. Вариант I (II)1. Запишите какую-нибудь формулу, задающую возрастающую
- 30. n.5.5 №791, №793, №794(а, в, д)Дома:
- 31. Вопросы учащимся:– Какая функция называется линейной?– Что
Слайд 3Устная работа
1. Даны уравнения. Какие из них задают прямую?
б) y = 3x² + 1; г) y = 3.
Слайд 5Устная работа
3. Укажите, у какой из следующих прямых
а) y = 2x + 5, y = 3x – 4, y = 0,7x + 1;
б) y = –3x + 1, y = –2x – 3, у = - 0,01х + 26.
Слайд 6Решение задач
Условия оплаты повременной телефонной связи в одном
Абонентская плата за месяц – 158 р.
Стоимость 1 минуты – 0,32 р.
Запишите формулу, выражающую зависимость стоимости
услуг телефонной связи за месяц с (в р.) от количество
минут разговора n.
c = 0,32 n + 158
Слайд 7Решение задач
Если тело движется с постоянным ускорением 0,2 см/с²,а
выражающую зависимость скорости движения v (в см/с) от
времени движения t (в с).
v = 4 + 0,2t
Слайд 8Решение задач
3. В баке легкового автомобиля 50 л бензина. На каждый
километр пути в среднем расходуется 0,07 л. Составьте
формулу, выражающую зависимость количество литров
бензина r , которое остаётся в баке после s ( в км ) пути .
r = 50 - 0,07s
Слайд 9Что общего во всех этих формулах?
c = 0,32 n + 158
r
Зависимости такого вида называются линейными функциями.
Слайд 10x – независимая переменная (аргумент)
y – зависимая переменная (функция)
Линейной называется функция,
Слайд 12Задание 2. Является ли функция линейной?
А) у = 5х – 1
Б) у=4(х - 3) - 2(х + 3);
В) у= х(4 + х) - 3х.
Устные задания
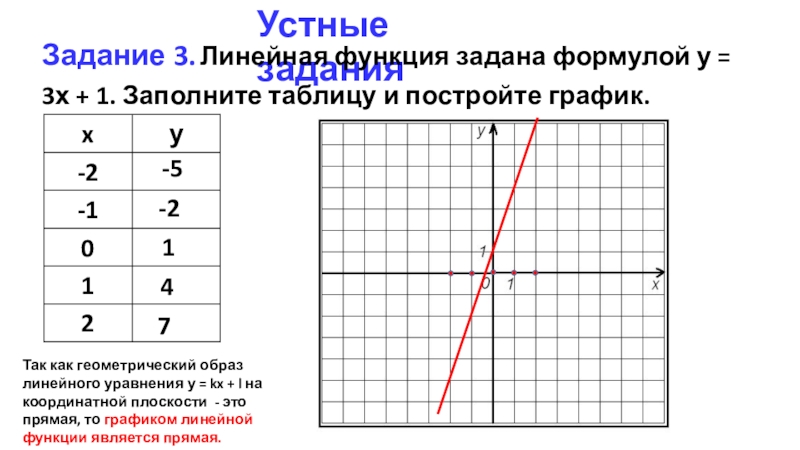
Слайд 13-5
-2
1
4
7
Устные задания
Задание 3. Линейная функция задана формулой у = 3х +
Так как геометрический образ линейного уравнения у = kx + l на координатной плоскости - это прямая, то графиком линейной функции является прямая.
Слайд 14Через две точки можно провести только одну прямую линию.
Для построения графика
Слайд 19k > 0 угол, образованный графиком функции и осью ОХ
х
y
Если правая рука выше левой, то угловой коэффициент положительный ( знак плюс)
Слайд 20k < 0 угол, образованный графиком функции и осью ОХ
x
y
Если левая рука выше правой, то угловой коэффициент отрицательный (знак минус)
Слайд 26
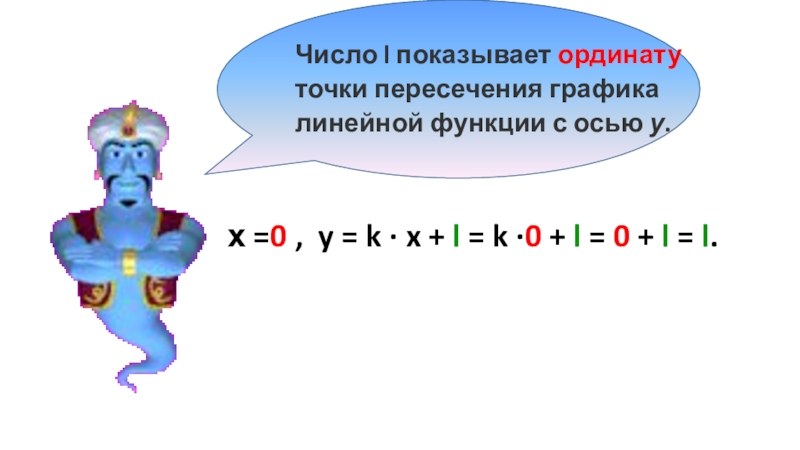
х =0 , y = k · x + l
Число l показывает ординату точки пересечения графика линейной функции с осью у.
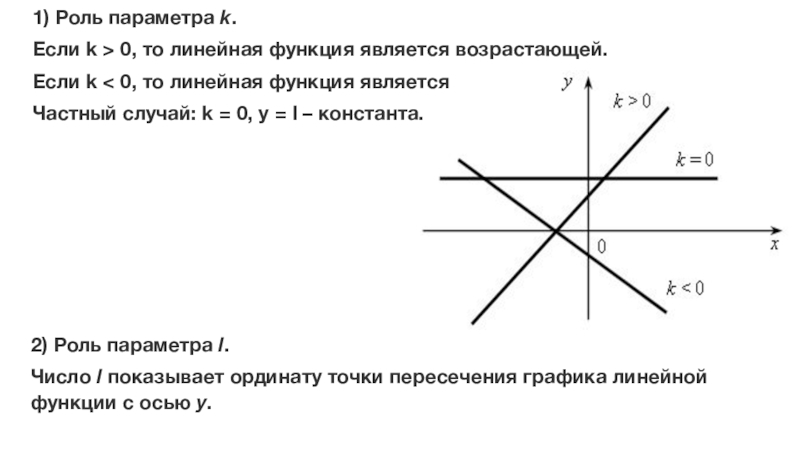
Слайд 271) Роль параметра k.
Если k > 0, то линейная функция является возрастающей.
Если k < 0,
Частный случай: k = 0, у = l – константа.
2) Роль параметра l.
Число l показывает ординату точки пересечения графика линейной функции с осью у.
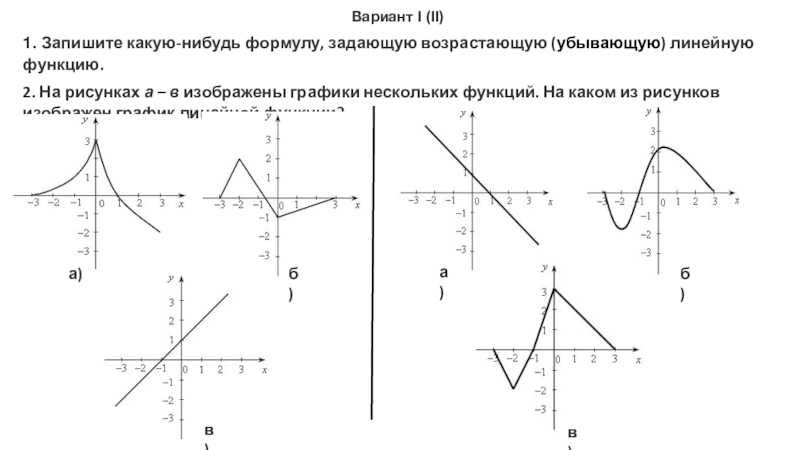
Слайд 29Вариант I (II)
1. Запишите какую-нибудь формулу, задающую возрастающую (убывающую) линейную функцию.
2. На
а)
а)
б)
б)
в)
в)
Слайд 31Вопросы учащимся:
– Какая функция называется линейной?
– Что является графиком линейной функции?
–
если k > 0; k< 0; k = 0?
- Какова роль параметра l в формуле линейной функции у = kx + l?
- При выполнении каких заданий вы испытывали затруднения?