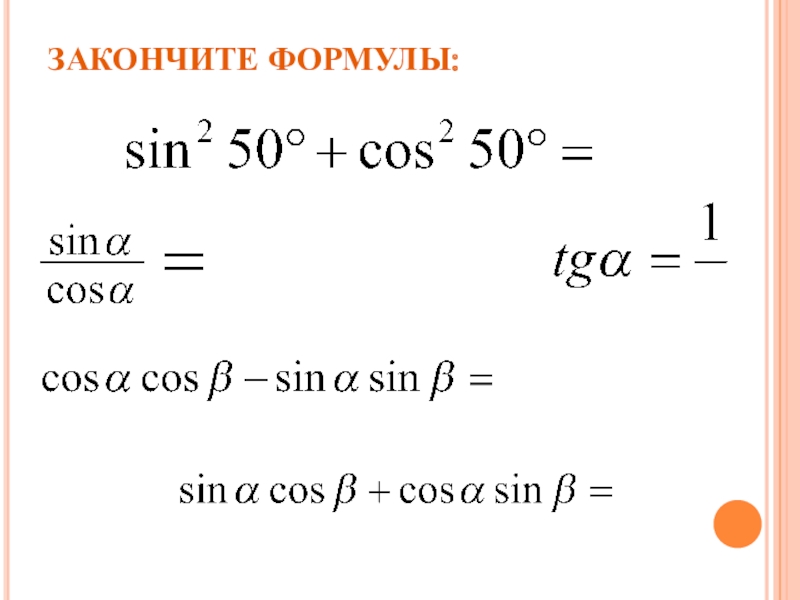- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Формулы приведения (10 класс)
Содержание
- 1. Презентация по алгебре на тему Формулы приведения (10 класс)
- 2. ФОРМУЛЫ ПРИВЕДЕНИЯПозволяют вычислить значения тригонометрических функций угла любой четверти через угол I четверти
- 3. ЗАКОНЧИТЕ ФОРМУЛЫ:
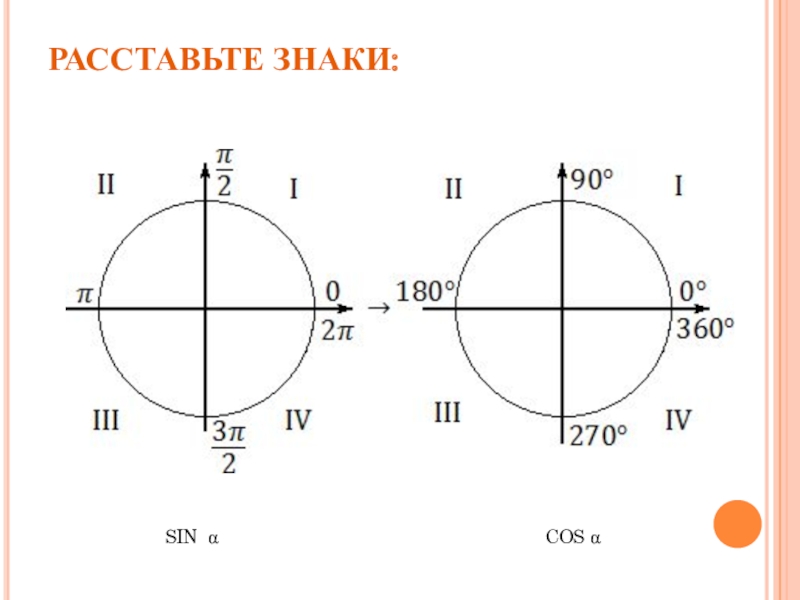
- 4. РАССТАВЬТЕ ЗНАКИ: SIN α COS α
- 5. ОПРЕДЕЛИТЕ ЧЕТВЕРТЬ:
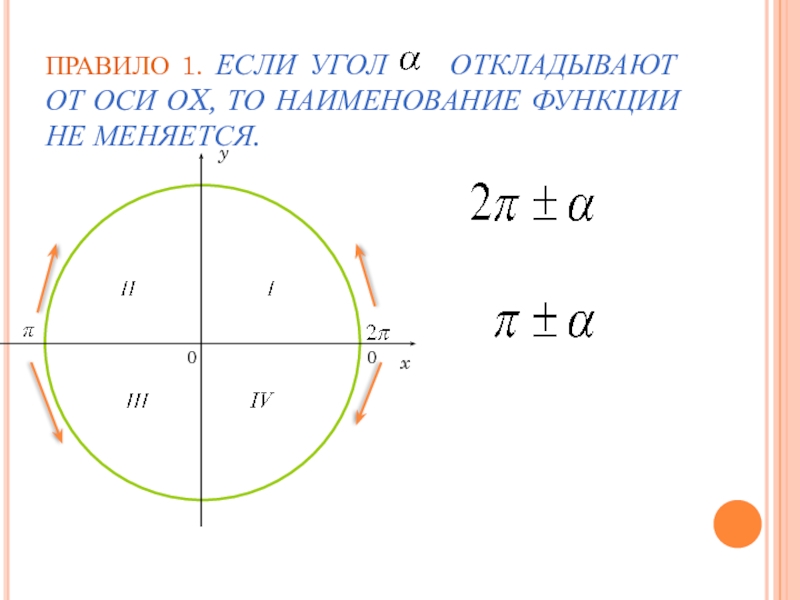
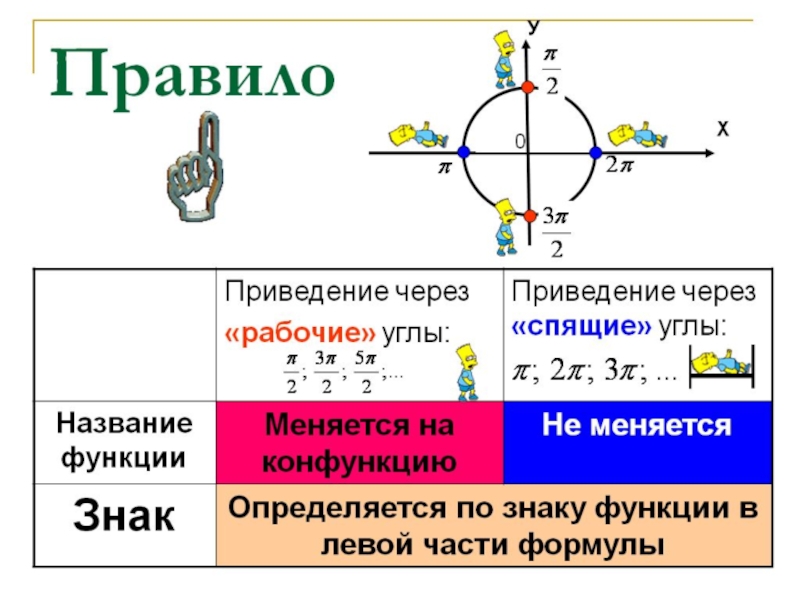
- 6. ПРАВИЛО 1. ЕСЛИ УГОЛ ОТКЛАДЫВАЮТ ОТ ОСИ ОX, ТО НАИМЕНОВАНИЕ ФУНКЦИИ НЕ МЕНЯЕТСЯ. 0xy0
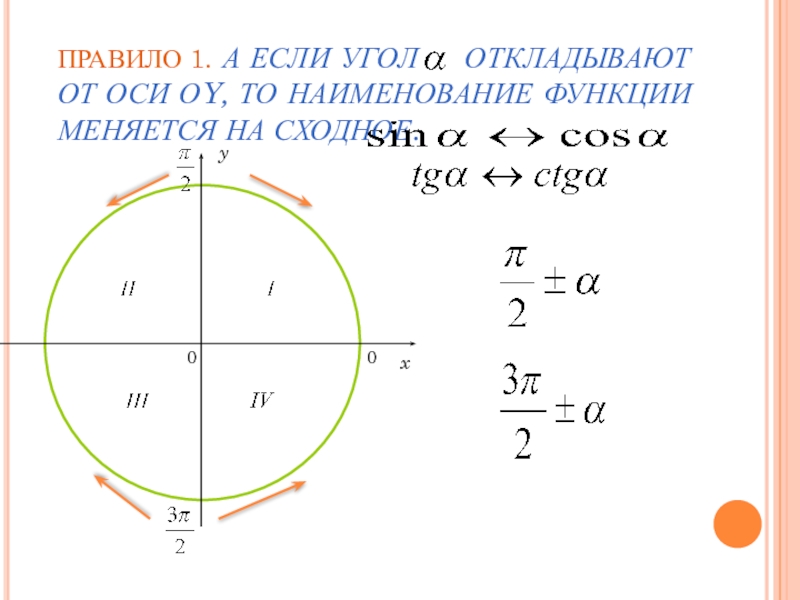
- 7. ПРАВИЛО 1. А ЕСЛИ УГОЛ
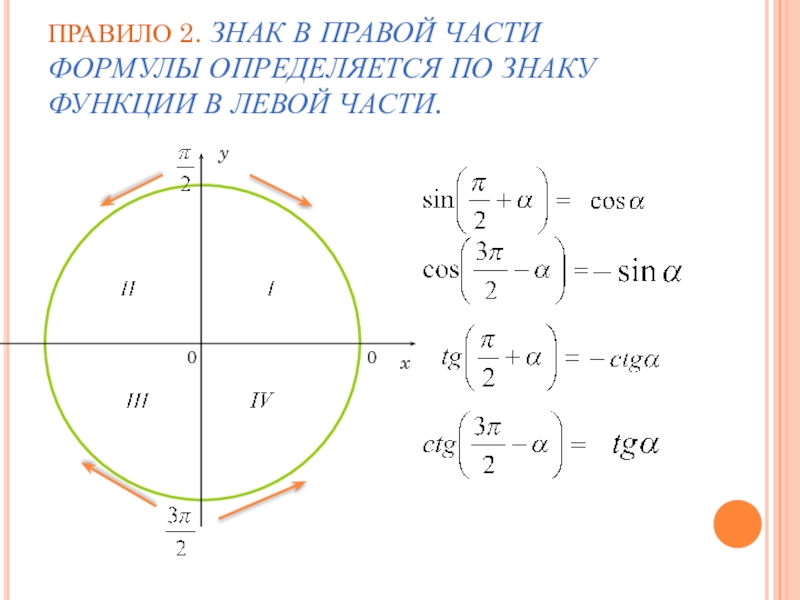
- 8. ПРАВИЛО 2. ЗНАК В ПРАВОЙ ЧАСТИ ФОРМУЛЫ ОПРЕДЕЛЯЕТСЯ ПО ЗНАКУ ФУНКЦИИ В ЛЕВОЙ ЧАСТИ.0xy0
- 9. ПРАВИЛО 2. ЗНАК В ПРАВОЙ ЧАСТИ ФОРМУЛЫ ОПРЕДЕЛЯЕТСЯ ПО ЗНАКУ ФУНКЦИИ В ЛЕВОЙ ЧАСТИ.0xy0
- 10. Слайд 10
- 11. Например: упростить sin (3π/2+α)
- 12. Упростить: sin (π+α) =
- 13. Слайд 13
- 14. Применение формул приведения :Для вычислений:
- 15. Эти формулы называются формулами приведения.Будем считать, что угол α – угол I четверти, т.е. α˂π/2
- 16. ЗАДАНИЕ 1.ВЫРАЗИТЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧЕРЕЗ УГОЛ МЕНЬШЕ 45°.
- 17. ЗАДАНИЕ 2. УПРОСТИТЕ ВЫРАЖЕНИЕ.
Слайд 2ФОРМУЛЫ ПРИВЕДЕНИЯ
Позволяют вычислить значения тригонометрических функций угла любой четверти через угол
Слайд 7ПРАВИЛО 1. А ЕСЛИ УГОЛ ОТКЛАДЫВАЮТ ОТ ОСИ ОY,
0
x
y
0
Слайд 10
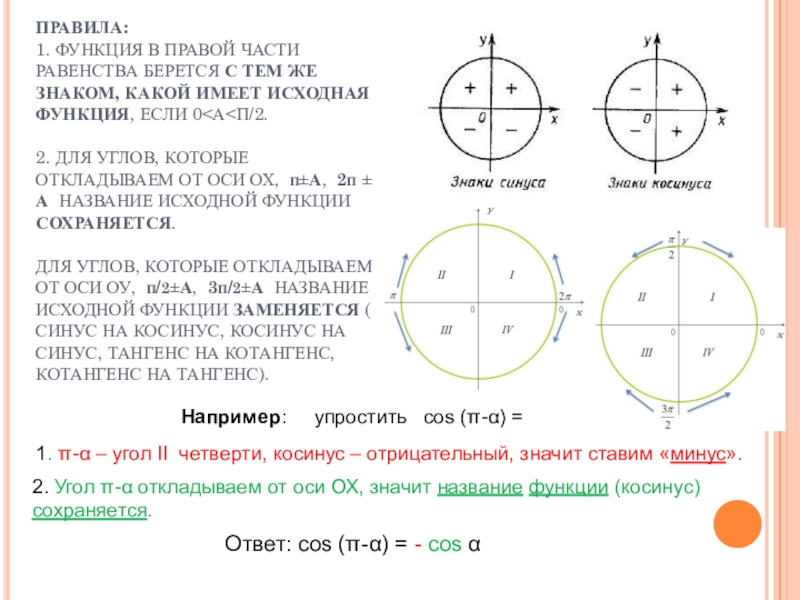
Ответ: cos (π-α) = - cos α
Например: упростить cos (π-α) =
1. π-α – угол II четверти, косинус – отрицательный, значит ставим «минус».
2. Угол π-α откладываем от оси ОХ, значит название функции (косинус) сохраняется.
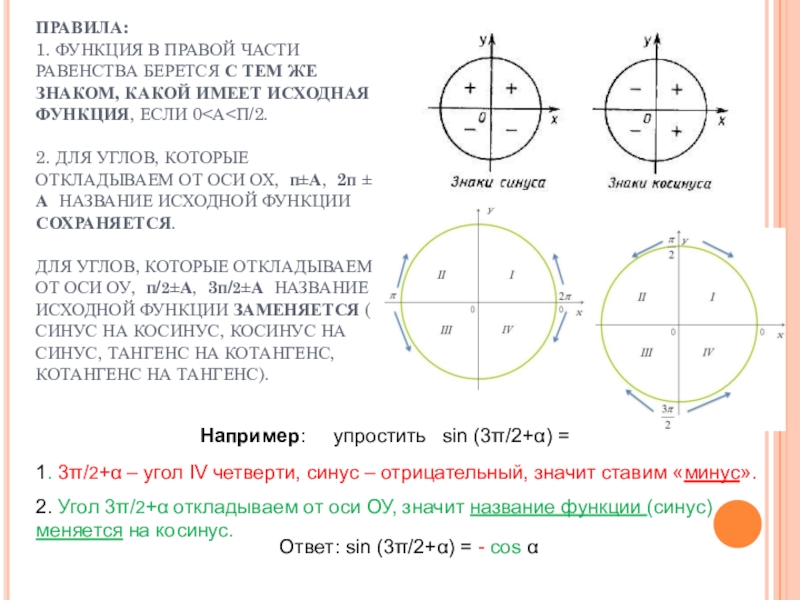
Слайд 11Например: упростить sin (3π/2+α) =
1. 3π/2+α –
2. Угол 3π/2+α откладываем от оси ОУ, значит название функции (синус) меняется на косинус.
Ответ: sin (3π/2+α) = - cos α
ПРАВИЛА:
1. ФУНКЦИЯ В ПРАВОЙ ЧАСТИ РАВЕНСТВА БЕРЕТСЯ С ТЕМ ЖЕ ЗНАКОМ, КАКОЙ ИМЕЕТ ИСХОДНАЯ ФУНКЦИЯ, ЕСЛИ 0<Α<Π/2.
2. ДЛЯ УГЛОВ, КОТОРЫЕ ОТКЛАДЫВАЕМ ОТ ОСИ ОХ, π±Α, 2π ± Α НАЗВАНИЕ ИСХОДНОЙ ФУНКЦИИ СОХРАНЯЕТСЯ.
ДЛЯ УГЛОВ, КОТОРЫЕ ОТКЛАДЫВАЕМ ОТ ОСИ ОУ, π/2±Α, 3π/2±Α НАЗВАНИЕ ИСХОДНОЙ ФУНКЦИИ ЗАМЕНЯЕТСЯ ( СИНУС НА КОСИНУС, КОСИНУС НА СИНУС, ТАНГЕНС НА КОТАНГЕНС, КОТАНГЕНС НА ТАНГЕНС).
Слайд 12Упростить:
sin (π+α) =
1). π+α –
2). Угол π+α откладываем от оси …, значит название функции (синус) …
Ответ: sin (π+α) = - sin α
cos (3π/2+α) =
1). В какой четверти угол?
2). От какой оси откладываем угол? Менять ли название функции?
Ответ: cos (3π/2+α) = sin α
sin (3π/2-α) =
1). В какой четверти угол?
2). От какой оси откладываем угол? Менять ли название функции?
Ответ: sin (3π/2-α) = - cos α