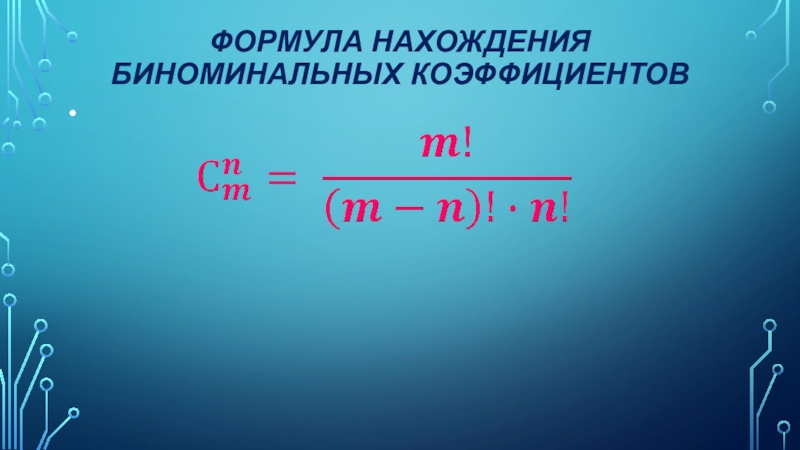А.Л.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Формулы сокращенного умножения для старших степеней (10 класс)
Содержание
- 1. Презентация по алгебре на тему Формулы сокращенного умножения для старших степеней (10 класс)
- 2. Формулы сокращенного умножения:(а + в)2 = а2+ 2ав
- 3. и для 5-ой степени:(а + в)5=Попробуйте записать формулу для 4-ой степени:(а + в)4=
- 4. Внимание!n = 0 (а +в)0 = 1n =
- 5. 1. число членов получаемого многочлена на единицу
- 6. Попробуем, используя полученные выводы, записать бином
- 7. Слайд 7
- 8. Слайд 8
- 9. Биноминальные коэффициенты можно вычислять по формуле. Бином Ньютона
- 10. Факториал натурального числа — произведение всех чисел
- 11. Формула нахождения биноминальных коэффициентов
- 12. =14 + 4·13·2а + 6·12·(2а)2 + 4· 11·(2а)3 + (2а)4 =1 + 8а + 24а2 + 32а3 + 16а4
- 13. Слайд 13
- 14. Слайд 14
Формулы сокращенного умножения:(а + в)2 = а2+ 2ав + в2 (а – в)2 = а2 – 2ав + в2 (а + в)3= а3 + 3а2в + 3ав2 + в3 (а – в)3= а3 – 3а2в + 3ав2 – в3
Слайд 1Формулы сокращенного умножения для старших степеней
Бином Ньютона
Учитель математики
ГБОУ Школа № 1592
Крайнюк
Слайд 2Формулы сокращенного умножения:
(а + в)2 = а2+ 2ав + в2
(а – в)2 =
а2 – 2ав + в2
(а + в)3= а3 + 3а2в + 3ав2 + в3
(а – в)3= а3 – 3а2в + 3ав2 – в3
Слайд 4Внимание!
n = 0 (а +в)0 = 1
n = 1 (а +в )1 =
1·а+1·в
n = 2 (а + в)2 = 1· а2+ 2·ав +1· в2
n = 3 ( а + в)3 = 1· а3 + 3·а2в + 3·ав2+1· в3
n = 4 ( а + в)4 = 1·а4 + 4·а3в + 6·а2в2+4·а в3 +1·в4
n = 5 (а + в)5 = 1·а5+ 5·а4в+ 10·а3в2+ 10·а2в3+ 5·ав4+ 1·в5
n = 2 (а + в)2 = 1· а2+ 2·ав +1· в2
n = 3 ( а + в)3 = 1· а3 + 3·а2в + 3·ав2+1· в3
n = 4 ( а + в)4 = 1·а4 + 4·а3в + 6·а2в2+4·а в3 +1·в4
n = 5 (а + в)5 = 1·а5+ 5·а4в+ 10·а3в2+ 10·а2в3+ 5·ав4+ 1·в5
Слайд 51. число членов получаемого многочлена на единицу больше показателя степени бинома;
2.
показатель степени первого слагаемого убывает от n до 0, показатель степени второго слагаемого возрастает от 0 до n;
3. степени всех одночленов равны степени двучлена в условии;
4. каждый одночлен является произведением первого и второго выражения в различных степенях и некоторого числа; числа– биноминальные коэффициенты;
5. биноминальные коэффициенты, равноотстоящие от начала и конца разложения, равны.
3. степени всех одночленов равны степени двучлена в условии;
4. каждый одночлен является произведением первого и второго выражения в различных степенях и некоторого числа; числа– биноминальные коэффициенты;
5. биноминальные коэффициенты, равноотстоящие от начала и конца разложения, равны.
Слайд 6Попробуем, используя полученные выводы,
записать бином для шестой степени.
«Треугольник Паскаля так
прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике.»
Мартин Гарднер
Мартин Гарднер
Слайд 10Факториал натурального числа — произведение всех чисел от единицы до этого
числа включительно, обозначается с помощью восклицательного знака: n!=1·2·3·4·...·n . Слово «факториал» латинское, переводится примерно как «производящий действие». Факториал очень быстро растёт с ростом числа. Так, 3!=6 , 7!=5040 , а 10!=3628800. Формулы, позволяющей быстро вычислить факториал без утомительного перемножения ряда чисел, не известно. Существует приближённая формула, найденная английским математиком XIX века Стирлингом: n!≈(n/e)n , где e≈2,7128K— основание натуральных логарифмов. Факториалы широко используются в комбинаторике и теории вероятностей.
Принято считать:
1! = 1
0! = 1