- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Элементы комбинаторики. Правило умножения. Урок 1 (9 класс)
Содержание
- 1. Презентация по алгебре на тему Элементы комбинаторики. Правило умножения. Урок 1 (9 класс)
- 2. Комбинаторика (лат. combinare) - «соединять, сочетать»Комбинаторика -
- 3. Задача. Сколько двузначных чисел можно составить из
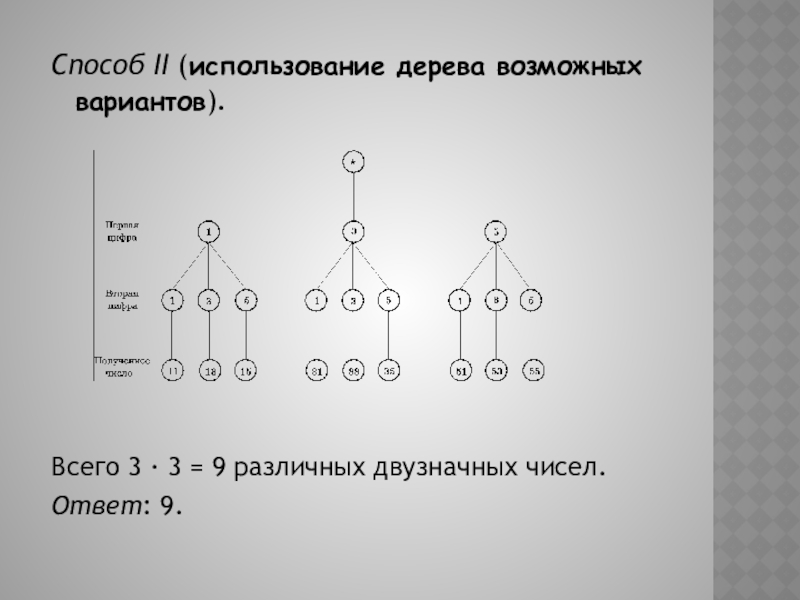
- 4. Способ II (использование дерева возможных вариантов).Всего 3 · 3 = 9 различных двузначных чисел. Ответ: 9.
- 5. Способ III (комбинаторное правило умножения) Ответ на
- 6. Комбинаторное правило умножения
- 7. Задача. Из города А в город В
- 8. № * Второй класс, в котором 23
- 9. Самостоятельная работа по теме «Правила умножения»1. Сколько трехзначных
- 10. Задание на дом1. Повторить п. 30.2. № 719, №724,
Слайд 1Элементы комбинаторики
(9 класс)
1 урок
Правило умножения
Составила
Учитель математики
МБОУ СОШ №41 г.Новосибирск
Яковлева О.Н.
Слайд 2Комбинаторика (лат. combinare) - «соединять, сочетать»
Комбинаторика - раздел математики, в котором
Слайд 3Задача. Сколько двузначных чисел можно составить из цифр 1, 3 и
Способ I (перебор возможных вариантов).
Первая цифра числа — номер строки, вторая цифра — номер столбца. Искомых чисел будет столько, сколько клеток в таблице, то есть 3 · 3 = 9.
Ответ: 9
Слайд 4Способ II (использование дерева возможных вариантов).
Всего 3 · 3 = 9
Ответ: 9.
Слайд 5Способ III (комбинаторное правило умножения)
Ответ на вопрос, поставленный в задаче,
Первую цифру можно выбрать тремя способами. Вторую цифру также можно выбрать тремя способами. Всего 3 · 3 = 9 различных двузначных чисел.
Ответ: 9.
Слайд 7Задача. Из города А в город В ведут две дороги, из
А В С Пристань
Решение.
Путь из А в В туристы могут выбрать 2 способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит 2⋅3 варианта маршрута из А в С. Т.к. из С на пристань можно попасть двумя способами, то всего существует 2⋅3⋅2 = 12 способов выбора туристами маршрута из города А к пристани.
Слайд 8№ * Второй класс, в котором 23 ученика, но мальчиков меньше,
Слайд 9Самостоятельная работа по теме «Правила умножения»
1. Сколько трехзначных чисел можно составить, используя
2. У Насти 3 брюк, 5 блузок и 2 кепки, удачно сочетающихся по цвету. Сколько различных комбинаций одежды она может составить?
3. Из Петербурга в Москву можно добраться на поезде, самолете, автобусе или теплоходе, а из Москвы во Владимир — на автобусе или электричке. Сколькими способами можно осуществить путешествие Петербург – Москва – Владимир?