- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Арксинус, арккосинус, арктангенс и арккотангенс числа
Содержание
- 1. Презентация по алгебре на тему Арксинус, арккосинус, арктангенс и арккотангенс числа
- 2. Теорема о корне.Пусть функция f возрастает (или
- 3. Функция у = sin x0Функция y=sin x возрастает на отрезке 1
- 4. аby=sin xФункция y=sin x возрастает на отрезке
- 5. Арксинусом числа а называется такое число из
- 6. Функция у = cos xФункция y=cos x убывает на отрезке 1ху
- 7. y=cos xФункция y=cos x убывает на отрезке
- 8. Арккосинусом числа а называется такое число из
- 9. Функция у = tg xФункция y=tgx возрастает на интервале
- 10. y=tg xаbаbФункция y=tg x возрастает на интервале
- 11. Арктангенсом числа а называется такое число из
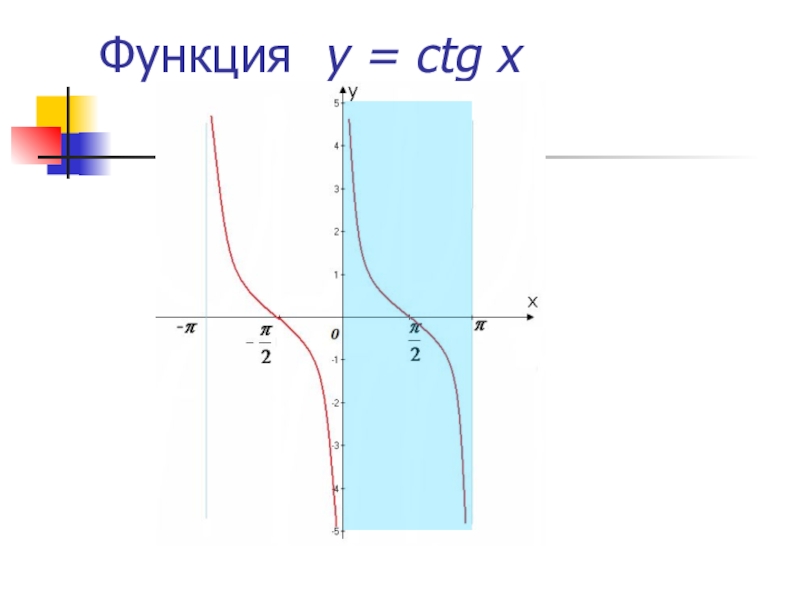
- 12. Функция у = сtg x
- 13. Арккотангенсом числа а называется такое число из
- 14. №1. Вычислите:1)2) 3)4)5)6)7)8)9)10)
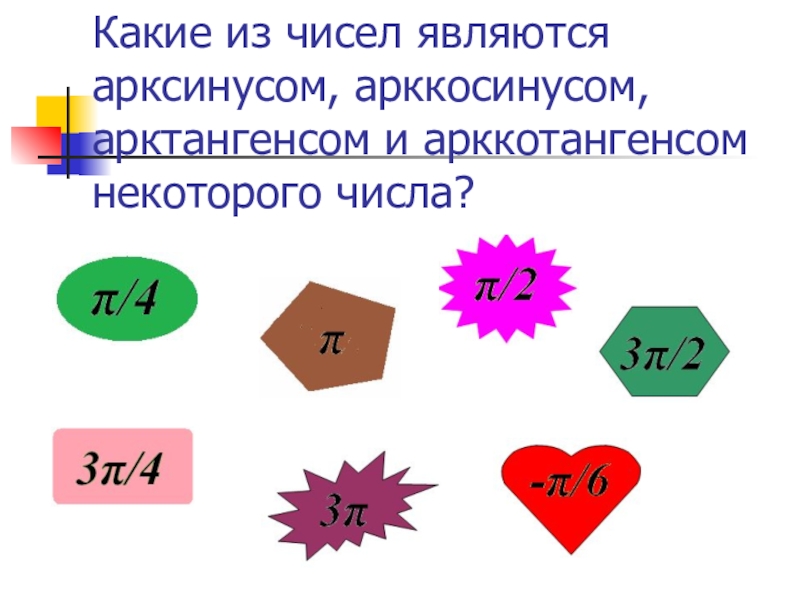
- 15. Какие из чисел являются арксинусом, арккосинусом, арктангенсом и арккотангенсом некоторого числа?
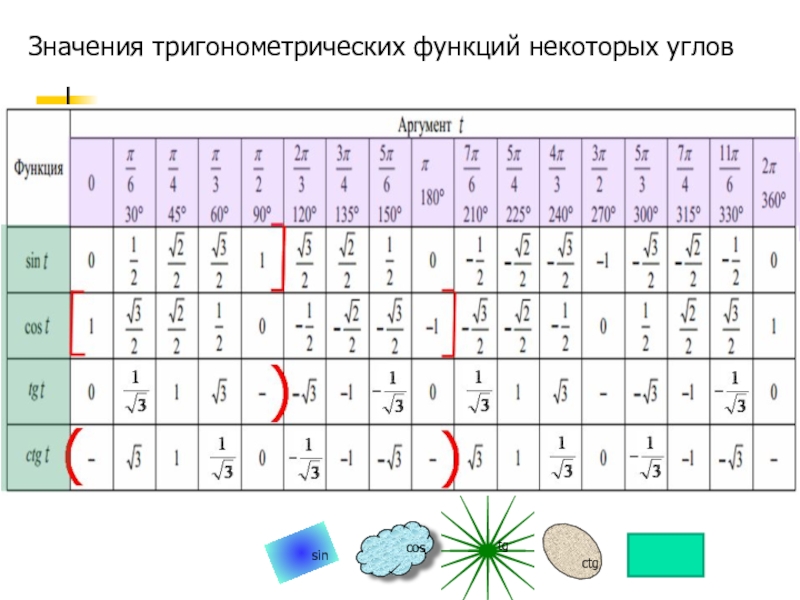
- 16. Значения тригонометрических функций некоторых угловsincostgctg
- 17. Домашнее задание. 1)Выучить определения арксинуса, арккосинуса, арктангенса
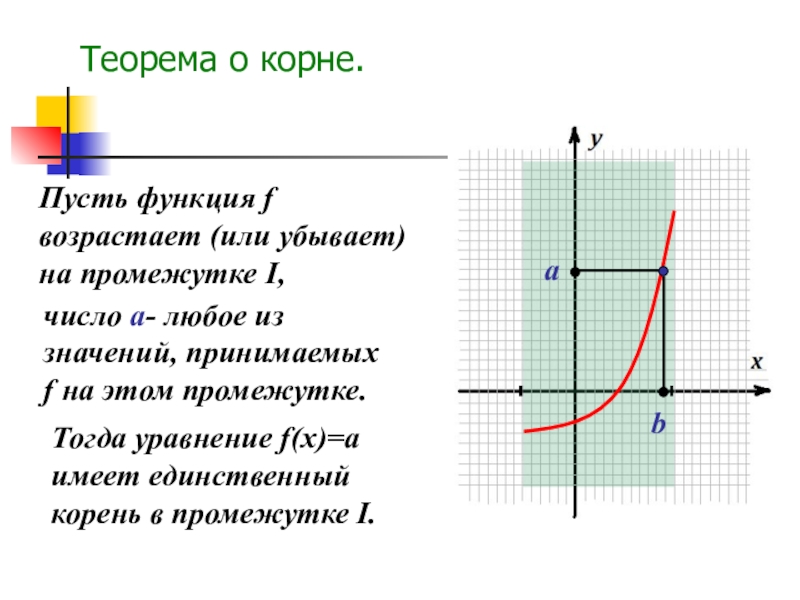
Слайд 2Теорема о корне.
Пусть функция f возрастает (или убывает) на промежутке I,
Тогда уравнение f(x)=a имеет единственный корень в промежутке I.
число a- любое из значений, принимаемых f на этом промежутке.
a
b
Слайд 4
а
b
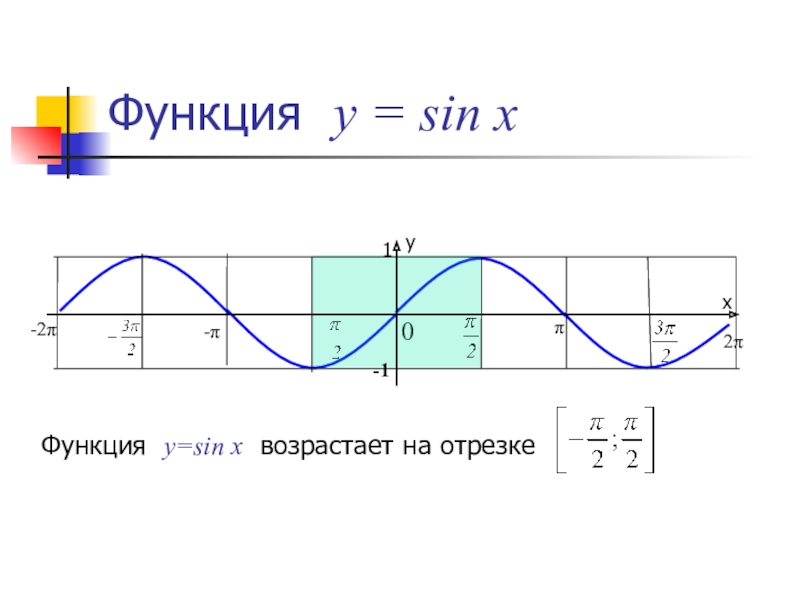
y=sin x
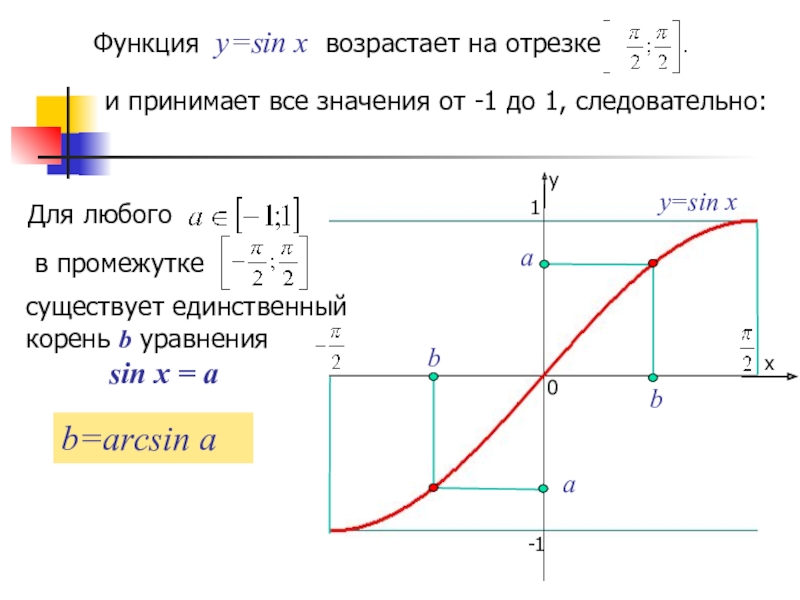
Функция y=sin x возрастает на отрезке
Для любого
в промежутке
существует
корень b уравнения
sin x = a
b=arcsin a
а
b
и принимает все значения от -1 до 1, следовательно:
Слайд 5
Арксинусом числа а называется такое число
из отрезка
, синус которого
arcsin а= t, если sint= а, где t , а
arcsin(-а)=-arcsin а
Пример:
arcsin
arcsin(-1)=
, так как sin
=
и
, так как sin
и
-arcsin1=
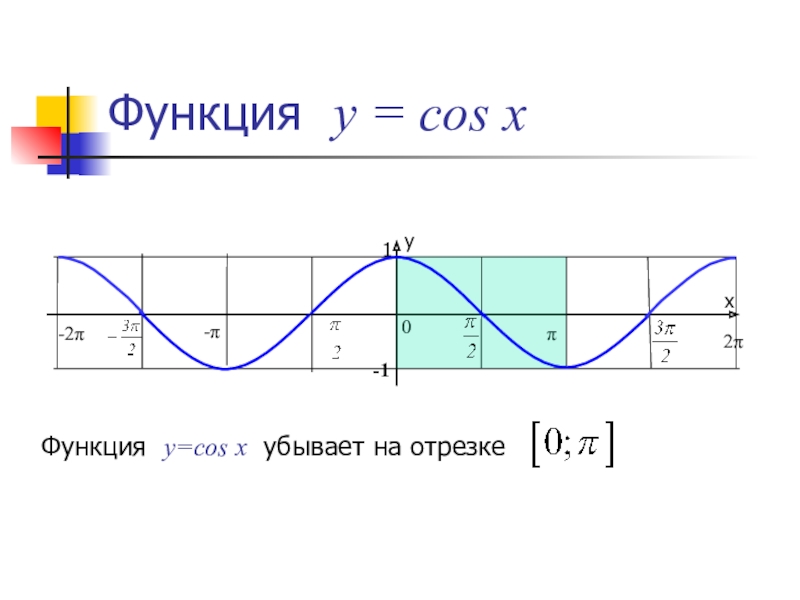
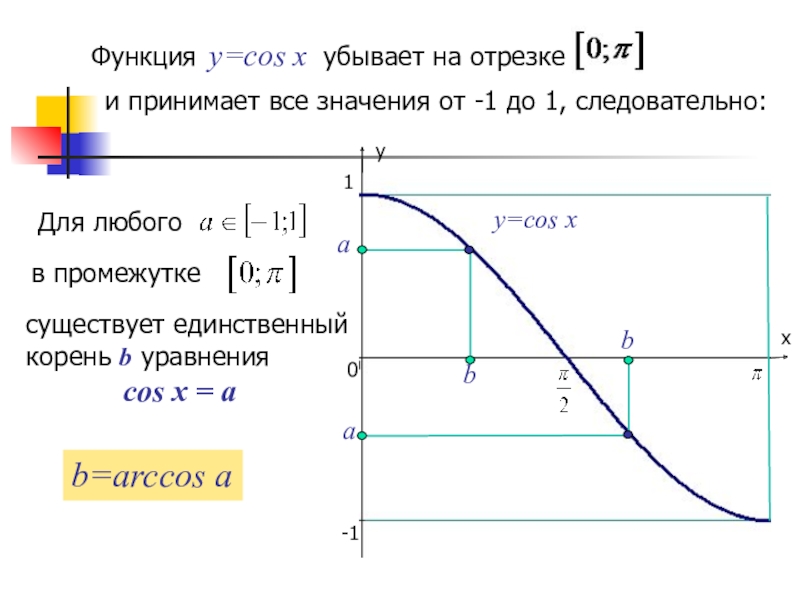
Слайд 7y=cos x
Функция y=cos x убывает на отрезке
Для любого
в промежутке
существует
корень b уравнения
cos x = a
b=arccos a
а
b
а
b
и принимает все значения от -1 до 1, следовательно:
Слайд 8
Арккосинусом числа а называется такое число
из отрезка
, косинус которого
arccos а= t, если cost= а, где t , а
Пример:
arccos
, так как cos
и
arccos(-1)=
, так как cos
и
Слайд 10
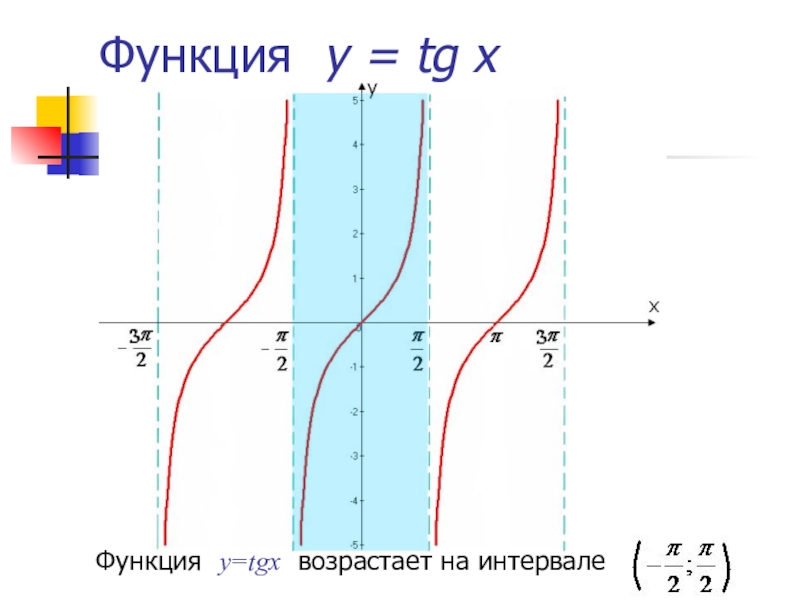
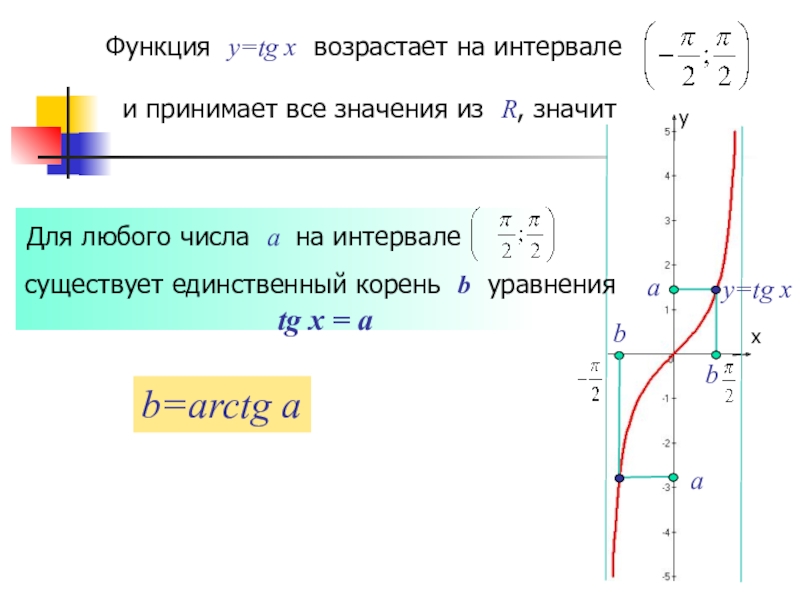
y=tg x
а
b
а
b
Функция y=tg x возрастает на интервале
Для любого числа а
существует единственный корень b уравнения
tg x = a
b=arctg a
и принимает все значения из R, значит
Слайд 11
Арктангенсом числа а называется такое число
из интервала
, тангенс которого равен
arctg а= t, если tgt= а, где t
arctg(-а)=-arctg а
Пример:
arctg
, так как tg
, где
arctg(-1)=
-arctg1=
, где
, так как tg
Слайд 13
Арккотангенсом числа а называется такое число
из интервала
, котангенс которого
arcctg а= t, если ctgt= а, где t
Пример:
arcctg
, так как ctg
, где
arcctg(-1)=
, где
, так как ctg
Слайд 15Какие из чисел являются арксинусом, арккосинусом, арктангенсом и арккотангенсом некоторого числа?
Слайд 17Домашнее задание.
1)Выучить определения арксинуса, арккосинуса, арктангенса и арккотангенса числа.
2) Сравнить
и
и
и
и