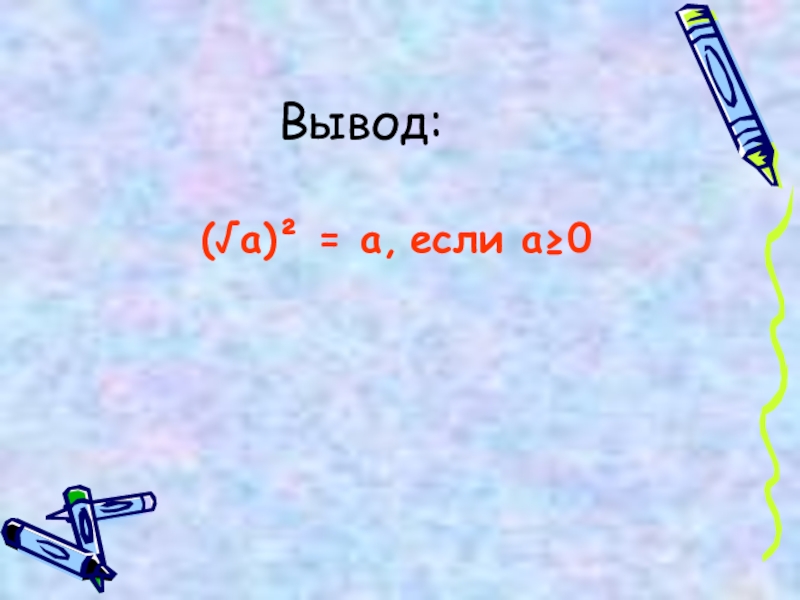- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Арифметический квадратный корень (8 класс)
Содержание
- 1. Презентация по алгебре на тему Арифметический квадратный корень (8 класс)
- 2. Установите к какому множеству относится число:5;
- 3. Слайд 3
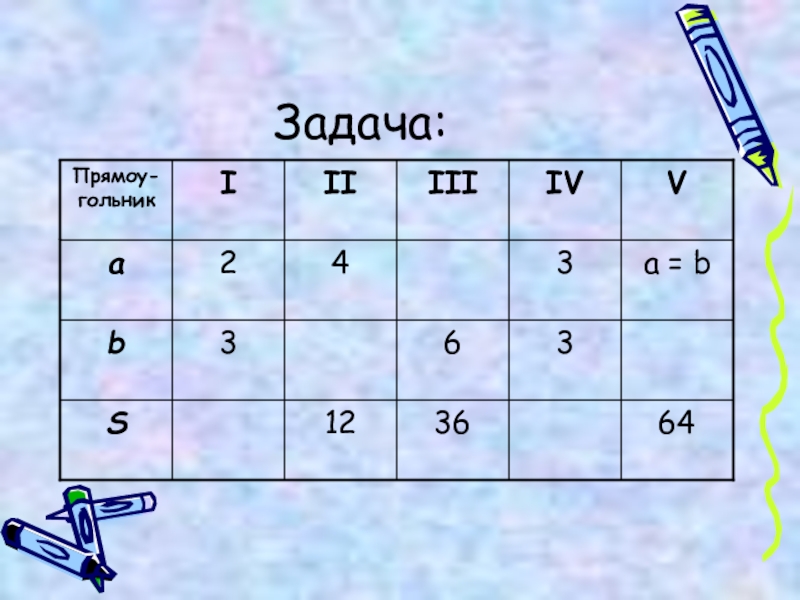
- 4. Задача:
- 5. Задание. Вместо пустых клеточек поставьте числа так, чтобы равенства были верными: 2=162=1\92=100
- 6. Определение:Квадратным корнем из числа аназывают число, квадрат которогоравен а.
- 7. Слайд 7
- 8. Определение: Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
- 9. √а – арифметический квадратный корень из числа
- 10. Задание: определить, является ли число n арифметическим
- 11. Историческая справка. Обратим внимание на совпадение в
- 12. Вычислите значения следующих выражений:
- 13. Вывод: (√а)² = а, если а≥0
- 14. Найдите значение арифметического квадратного корня:а)
- 15. Эталон: а) 7; б)
- 16. Задание 1:Найдите значение выражения:а)
- 17. Задание 2:Укажите натуральные значения n, прикоторых является натуральным числомзначение выражения
- 18. Подведение итогов Что называется квадратным корнем из
- 19. Домашнее заданиеДля тех, кто хочет, чтобы изучение
- 20. Желаю вам дальнейших успехов в изучении математики !
Установите к какому множеству относится число:5; 0; - 4,7; π; -7; 3,5?
Слайд 1Тема: Квадратный корень.Арифметический квадратный корень
Цели:
1 .Ввести понятие квадратного корня из числа
а и определение арифметического квадратного корня из числа а .Закрепить эти понятия в ходе выполнения упражнений
2 .Выработка навыков устного вычисления
3 Развитие логического мышления
2 .Выработка навыков устного вычисления
3 Развитие логического мышления
Слайд 5Задание. Вместо пустых клеточек поставьте числа так, чтобы равенства были верными:
2=16
2=1\9
2=100
Слайд 7 Задание: выяснить, является ли число n квадратным корнем из числа m,
если:
а) n = 5, m = 25; в) n = 0,3, m = 0,9;
б) n = - 7, m = 49; г) n = 6, m = - 36.
Слайд 8Определение:
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат
которого равен а.
Слайд 9
√а – арифметический квадратный корень из числа а
√а ≥ 0
(√а)2 = а
√ - знак арифметического квадратного корня
а – подкоренное выражение,
где а ≥ 0
Слайд 10Задание: определить, является ли число n арифметическим квадратным корнем из числа
m, если:
а) n = 8, m = 64; в) n = 0,2, m = 0,4;
б) n = - 3, m = 9; г) n = 0,4, m = 0,16.
Слайд 11Историческая справка.
Обратим внимание на совпадение в терминах — квадратный корень и
корень уравнения. Это совпадение неслучайно. Уравнения вида х²=а исторически были первыми сложными уравнениями, и их решения были названы корнями по метафоре, что из стороны квадрата, как из корня, вырастает сам квадрат. В дальнейшем термин «корень» стал употребляться и для произвольных уравнений.
Название «радикал» тоже связано с термином «корень»: по-латыни корень — radix (он же редис — корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа √ связывают с написанием латинской буквы r.
Название «радикал» тоже связано с термином «корень»: по-латыни корень — radix (он же редис — корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа √ связывают с написанием латинской буквы r.
Слайд 17Задание 2:
Укажите натуральные значения n, при
которых является натуральным числом
значение выражения
Слайд 18Подведение итогов
Что называется квадратным корнем из числа а?
Сколько квадратных корней может
быть из числа а?
Что такое арифметический квадратный корень из числа а?
Имеет ли смысл запись ? Почему?
Что такое арифметический квадратный корень из числа а?
Имеет ли смысл запись ? Почему?
Слайд 19Домашнее задание
Для тех, кто хочет, чтобы изучение математики было успешным:
Прочитать П.12;
Решить: № 301, № 304, № 306(в; г).