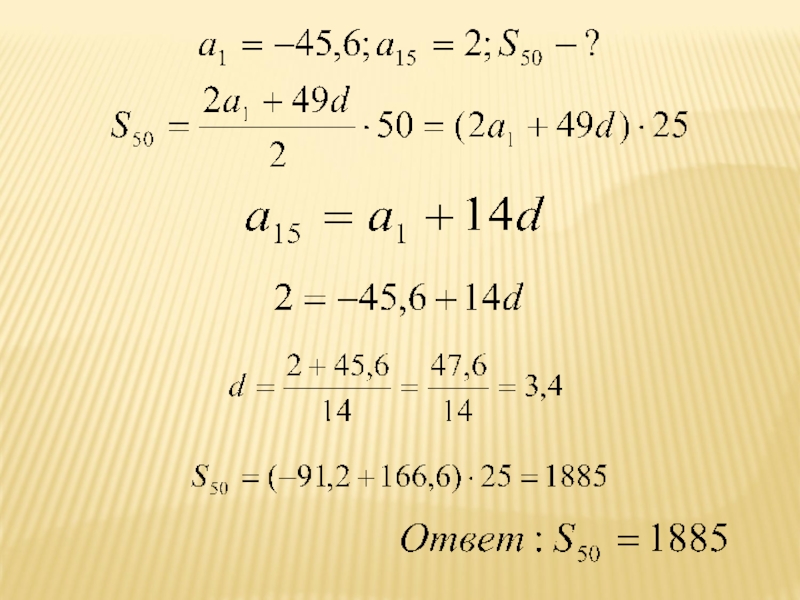- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Арифметическая и геометрическая прогрессии
Содержание
- 1. Презентация по алгебре на тему Арифметическая и геометрическая прогрессии
- 2. Сегодня мы узнаем:определения арифметической и геометрической прогрессий;
- 3. Немного из историиСлово «прогрессия» латинского происхождения (progressio),
- 4. Арифметической прогрессией называется последовательность, каждый член
- 5. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов.Арифметическая прогрессия
- 6. Геометрической прогрессией называется последовательность отличных от
- 7. Геометрическая прогрессияКаждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому двух соседних с ним членов.
- 8. Формула n – го члена арифметической прогрессии
- 9. Формула n – го члена геометрической прогрессии
- 10. Найдите сумму пятидесяти первых членов арифметической прогрессии,
- 11. Формула суммы n первых членов арифметической прогрессии
- 12. Слайд 12
- 13. Формула суммы n первых членов геометрической прогрессииБесконечно убывающая геометрическая прогрессия
- 14. Спасибо за урок!
Сегодня мы узнаем:определения арифметической и геометрической прогрессий; формулы n- го члена арифметической и геометрической прогрессий; формулы суммы n первых членов прогрессий.
Слайд 2Сегодня мы узнаем:
определения арифметической и
геометрической прогрессий;
формулы n- го
члена арифметической и
геометрической прогрессий;
формулы суммы n первых членов
прогрессий.
геометрической прогрессий;
формулы суммы n первых членов
прогрессий.
Слайд 3Немного из истории
Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед»
( как и слово «прогресс») и
встречается впервые у римского автора Боэция (V-VI вв.).
Задачи на геометрические и арифметические прогрессии встречаются у вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах». На связь между прогрессиями первым обратил внимание Архимед.
.
встречается впервые у римского автора Боэция (V-VI вв.).
Задачи на геометрические и арифметические прогрессии встречаются у вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах». На связь между прогрессиями первым обратил внимание Архимед.
.
Слайд 4 Арифметической прогрессией
называется последовательность,
каждый член которой, начиная со второго,
равен предыдущему члену,
сложенному с одним и тем же числом.
сложенному с одним и тем же числом.
Слайд 5Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух
соседних с ним членов.
Арифметическая прогрессия
Слайд 6 Геометрической прогрессией
называется последовательность
отличных от нуля чисел,
каждый член
которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
Слайд 7Геометрическая прогрессия
Каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому
двух соседних с ним членов.
Слайд 10Найдите сумму пятидесяти первых членов
арифметической прогрессии,
первый член которой
равен
– 45,6,
а пятнадцатый член равен 2.
а пятнадцатый член равен 2.
Слайд 13Формула суммы n первых членов
геометрической прогрессии
Бесконечно убывающая геометрическая прогрессия
