Учитель:
Караматуллина Флюзя Хаматхановна
г. Янаул
2016 г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Методы решения тригонометрических уравнений (10 класс)
Содержание
- 1. Презентация по алгебре Методы решения тригонометрических уравнений (10 класс)
- 2. Графический диктант (----- да, ^ нет)
- 3. 1). уравнение вида Аsinx + Bcosx
- 4. КЛЮЧ ДЛЯ ПРОВЕРКИ: ----- ^ ^ ----- ------ ^ ----- ^----- ----- ---- ^
- 5. Выбрать решаемые:а) делением cosx ≠ 0 б)
- 6. Ключ для проверки:а) 2, 5, 9б) 3в)
- 7. «ТРИГОНОМЕТРИЯ В ОКРУЖАЮЩЕМ НАС МИРЕ И ЖИЗНИ ЧЕЛОВЕКА»
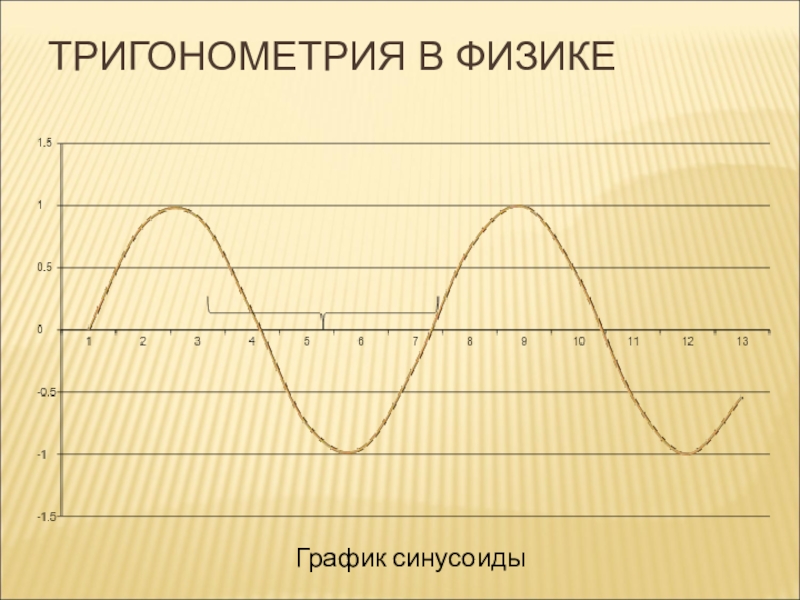
- 8. ТРИГОНОМЕТРИЯ В ФИЗИКЕГрафик синусоиды
- 9. МАТЕМАТИЧЕСКИЙ МАЯТНИКНа рисунке изображены колебания маятника, он движется по кривой, называемой косинусом.
- 10. Формулы колебаний:где A – амплитуда колебания,
- 11. ТРАЕКТОРИЯ ПУЛИ И ПРОЕКЦИИ ВЕКТОРОВ НА ОСИ
- 12. Радуга возникает из-за того,
- 13. ТРИГОНОМЕТРИЯ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В МЕДИЦИНЕ И
- 14. МОДЕЛЬ БИОРИТМОВ.Для построения модели биоритмов необходимо ввести
- 15. ОПИСАНИЕ ДВИЖЕНИЯ РЫБ В ВОДЕ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
- 16. У МУЗЫКИ ЕСТЬ СВОЯ ГЕОМЕТРИЯТетраэдр из различных
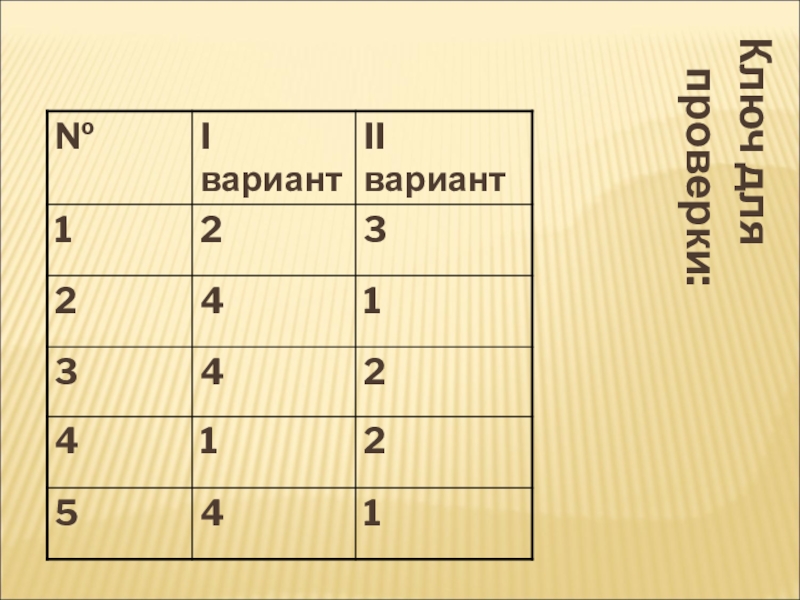
- 17. Ключ для проверки:
- 18. Спасибо за внимание!
Графический диктант (----- да, ^ нет)
Слайд 31). уравнение вида Аsinx + Bcosx = C, где А,
В, С - данные числа и А,В≠0 решается методом введение вспомогательного угла,
2). уравнение cosx = 0 имеет одну серию решений X = π /2+2πk , k € Z ,
3). при а < -1 неравенство sinx > а не имеет решений,
4). уравнения, содержащие чётную степень sin или cos, решается выражением sin через cos или cos через sin ,
5). простейшие тригонометрические уравнение удобно решать с помощью единичной окружности,
6). при а < -1 неравенство cos x > а не имеет решений
7). при любом а € R множество всех решений неравенства tgx8). при любом а € R множество всех решений неравенства сtgx9). уравнения, приводящиеся к однородному, решается тригонометрическим разложением единицы,
10). уравнение sinx + cosx =0 равносильно уравнения tgx +1 = 0,
11). при решении дробно-рациональных тригонометрических уравнений необходимо исключить корни знаменателя,
12). при а > 1 неравенство cos x < а не имеет решений
2). уравнение cosx = 0 имеет одну серию решений X = π /2+2πk , k € Z ,
3). при а < -1 неравенство sinx > а не имеет решений,
4). уравнения, содержащие чётную степень sin или cos, решается выражением sin через cos или cos через sin ,
5). простейшие тригонометрические уравнение удобно решать с помощью единичной окружности,
6). при а < -1 неравенство cos x > а не имеет решений
7). при любом а € R множество всех решений неравенства tgx8). при любом а € R множество всех решений неравенства сtgx9). уравнения, приводящиеся к однородному, решается тригонометрическим разложением единицы,
10). уравнение sinx + cosx =0 равносильно уравнения tgx +1 = 0,
11). при решении дробно-рациональных тригонометрических уравнений необходимо исключить корни знаменателя,
12). при а > 1 неравенство cos x < а не имеет решений
Слайд 5Выбрать решаемые:
а) делением cosx ≠ 0
б) сведением к простейшим заменой
неизвестного
в) делением на сos2 x ≠ 0
г) применением основного тригонометрического тождества
д) применением формул сложения
е) понижением степени уравнения
ж) введением вспомогательного угла
Отобрать:
з) уравнения, неравенства, для решения которых требуются, так называемые, специальные приёмы
и) уравнения и неравенства, которые не попали под описание и мы ещё такие не решали
в) делением на сos2 x ≠ 0
г) применением основного тригонометрического тождества
д) применением формул сложения
е) понижением степени уравнения
ж) введением вспомогательного угла
Отобрать:
з) уравнения, неравенства, для решения которых требуются, так называемые, специальные приёмы
и) уравнения и неравенства, которые не попали под описание и мы ещё такие не решали
Слайд 9МАТЕМАТИЧЕСКИЙ МАЯТНИК
На рисунке изображены колебания маятника, он движется по кривой, называемой
косинусом.
Слайд 10Формулы колебаний:
где A – амплитуда колебания, - угловая
частота колебания,
- начальная фаза
колебания, - фаза колебания.
колебания, - фаза колебания.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
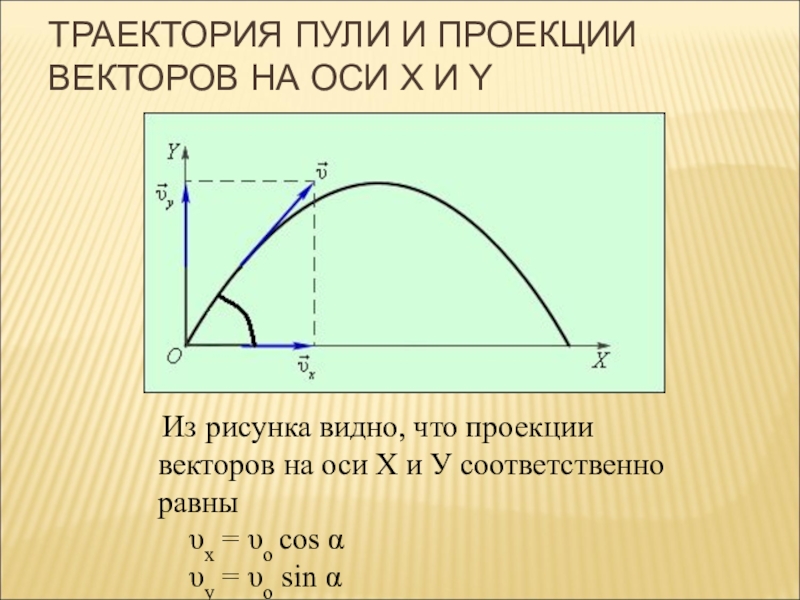
Слайд 11ТРАЕКТОРИЯ ПУЛИ И ПРОЕКЦИИ ВЕКТОРОВ НА ОСИ X И Y
Из
рисунка видно, что проекции векторов на оси Х и У соответственно равны
υx = υo cos α
υy = υo sin α
υx = υo cos α
υy = υo sin α
Слайд 12 Радуга возникает из-за того, что солнечный свет испытывает
преломление в капельках воды, взвешенных в воздухе по закону преломления:
n1 - показатель преломления первой среды n2 - показатель преломления второй среды
α-угол падения, β-угол преломления света
n1 - показатель преломления первой среды n2 - показатель преломления второй среды
α-угол падения, β-угол преломления света
sin α / sin β = n1 / n2
ТЕОРИЯ РАДУГИ
Слайд 13ТРИГОНОМЕТРИЯ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В МЕДИЦИНЕ И БИОЛОГИИ.
Одно из фундаментальных свойств
живой природы - это цикличность большинства происходящих в ней процессов.
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Основной земной ритм – суточный.
Модель биоритмов можно построить с помощью тригонометрических функций.
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Основной земной ритм – суточный.
Модель биоритмов можно построить с помощью тригонометрических функций.
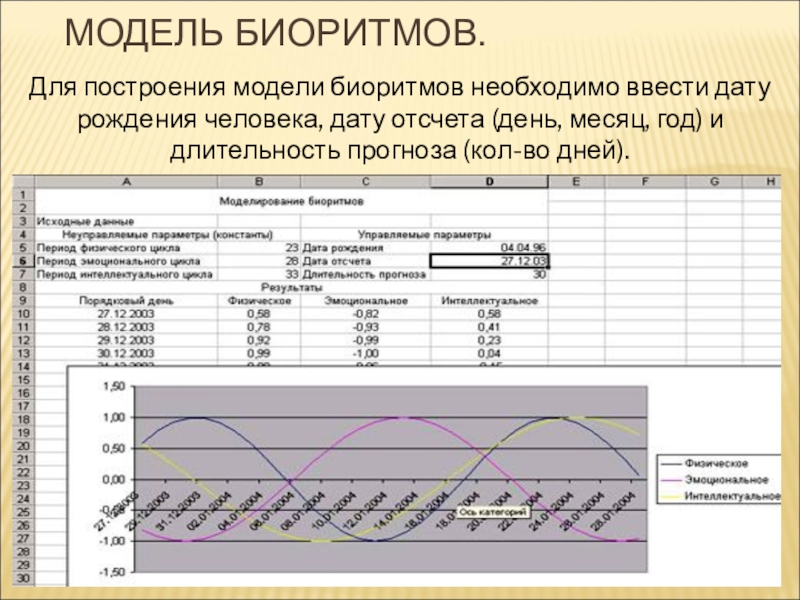
Слайд 14МОДЕЛЬ БИОРИТМОВ.
Для построения модели биоритмов необходимо ввести дату рождения человека, дату
отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
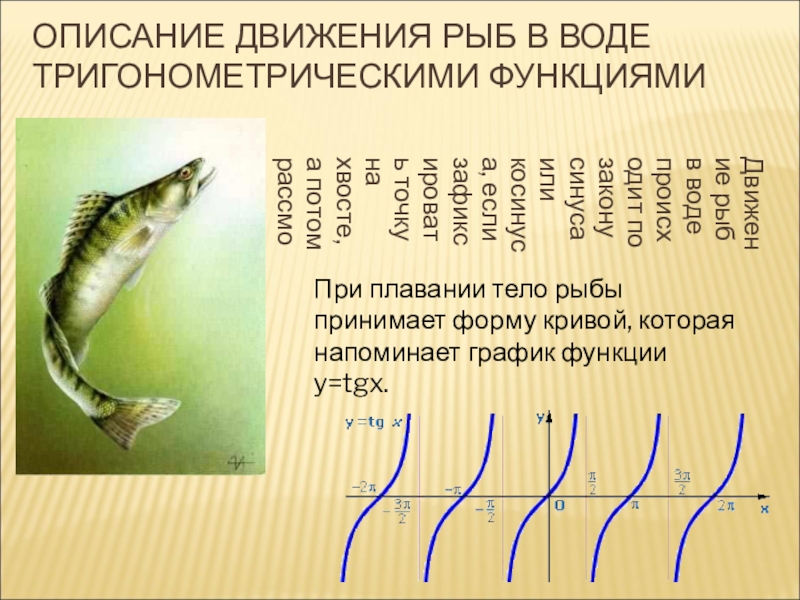
Слайд 15ОПИСАНИЕ ДВИЖЕНИЯ РЫБ В ВОДЕ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
Движение рыб в
воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Слайд 16У МУЗЫКИ ЕСТЬ СВОЯ ГЕОМЕТРИЯ
Тетраэдр из различных типов аккордов четырех звуков:
синий
– малые интервалы;
более теплые тона - более «разряженные» звуки аккорда; красная сфера- наиболее гармоничный аккорд с равными интервалами между нотами.
более теплые тона - более «разряженные» звуки аккорда; красная сфера- наиболее гармоничный аккорд с равными интервалами между нотами.