- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Методы решения систем двух линейных уравнений с двумя переменными
Содержание
- 1. Презентация по алгебре Методы решения систем двух линейных уравнений с двумя переменными
- 2. «Кто приобрёл навык общаться легко и свободно
- 3. Задачи:обобщить знания по теме «Методы решения систем
- 4. Историческая справка.Основные понятия.Графический метод.Метод подстановки.Метод алгебраического сложения.Правило Крамера.Системы линейных уравнений с параметрами. Содержание проекта:
- 5. Механическое правило решения систем двух линейных уравнений
- 6. Франсуа Виет - французский математик. По профессии
- 7. Габриэ́ль Кра́мер (31 июля 1704, Женева, Швейцария—4
- 8. Общий вид системы двух линейных уравнений с
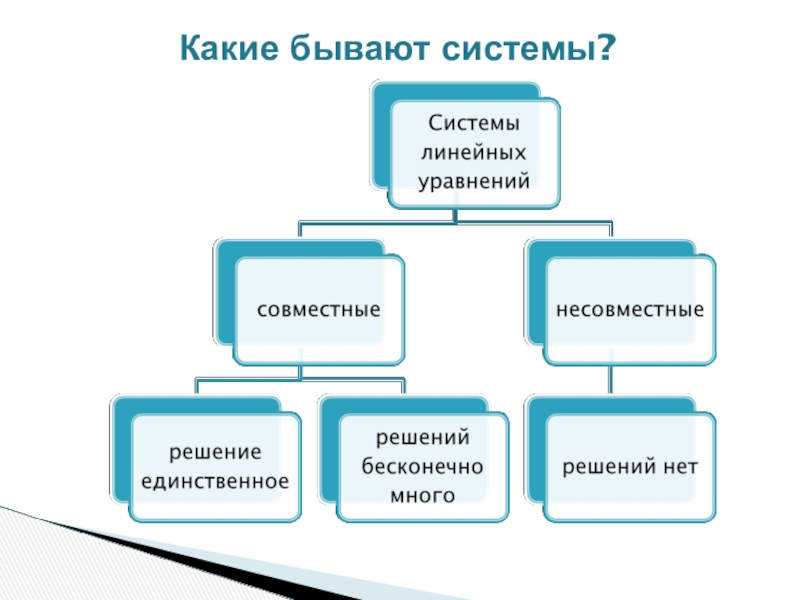
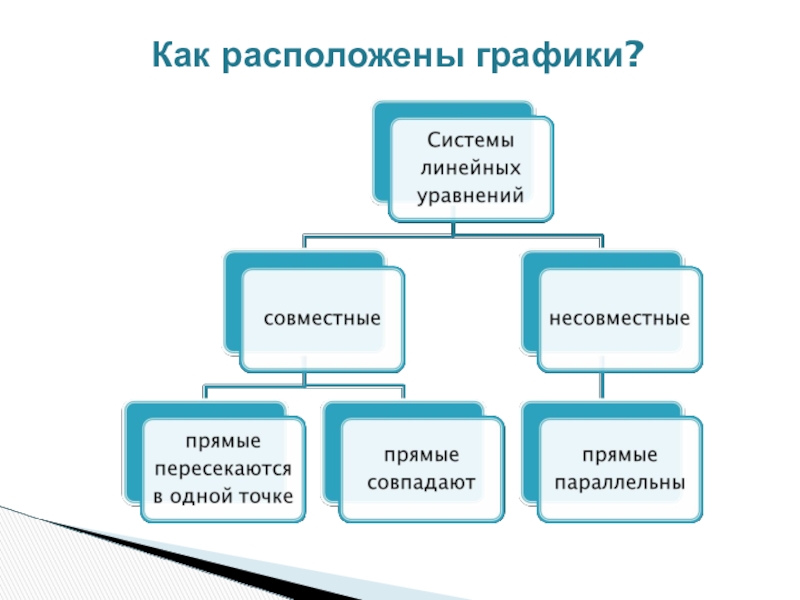
- 9. Какие бывают системы?
- 10. графический метод; метод подстановки; метод алгебраического
- 11. Графический метод решения систем, как и графический
- 12. В уравнениях системы выразить y через x
- 13. 2Решение:В уравнениях системы выразить y через x:а)
- 14. 2Прямые пересекаются в точке (1;2)4) Проверка показывает,
- 15. Решение:В уравнениях системы выразить y через x:
- 16. Решение:В уравнениях системы выразить y через x:а)
- 17. Слайд 17
- 18. Как расположены графики?
- 19. Метод постановки – это универсальный алгебраический метод.
- 20. Выразить y через x из первого уравнения
- 21. Решение:Выразим x через y из второго уравнения:
- 22. 4) Подставим найденное значение y в формулу
- 23. Систему уравнений легче решать методом сложения, когда
- 24. Преобразовать коэффициенты так, чтобы коэффициенты при x
- 25. Решение:Умножив первое уравнение на 5, а второе
- 26. 3) Решим полученное уравнение.25x + 8x =
- 27. Матрица- Определитель- Правило Крамера
- 28. 1) Если главный определитель ∆≠ 0, то
- 29. Решение:Найдём определители системы:
- 30. Решение:Найдём определители системы:∆ =
- 31. Решение:Найдём определители системы:∆=
- 32. Параметр, будучи фиксированным, но неизвестным числом, имеет
- 33. Система двух линейных алгебраических уравнений с двумя неизвестными в параметрах.
- 34. Дана система уравненийИзвестно, что пара чисел (2;-1)
- 35. Сложим получившиеся уравнения:2a +2a -1b + 1b=
- 36. Если а =0, то имеем уравнение 0·х
- 37. Решение: Из второго уравнения найдём х=1–аy
- 38. 2) a= -3. Тогда 3(-3 + 3)
- 39. Решение: Найдём определители системы:∆ =
- 40. ∆ = а(2 - а) ≠ 0
- 41. б) при а = 2 определитель а(11а
- 42. Алгебра: Учеб. Для 7 кл. общеобразоват. учреждений
Слайд 2«Кто приобрёл навык общаться легко и свободно со всевозможными алгебраическими и
Д.И.Писарев
Слайд 3Задачи:
обобщить знания по теме «Методы решения систем двух линейных уравнений с
расширить представления о методах решения систем двух линейных уравнений с двумя переменными;
продолжить формирование информационных навыков с научными текстами, коммуникативных – работе в паре, в группе;
воспитывать волю и настойчивость при решении систем уравнений
Цель: систематизировать знания по теме «Методы решений систем двух линейных уравнений с двумя переменными».
Слайд 4Историческая справка.
Основные понятия.
Графический метод.
Метод подстановки.
Метод алгебраического сложения.
Правило Крамера.
Системы линейных уравнений с
Содержание проекта:
Слайд 5Механическое правило решения систем двух линейных уравнений по их коэффициентам
(с
"О великом искусстве"
в 1545 году итальянский математик Джероламо Кардано.
Историческая справка
Слайд 6Франсуа Виет - французский математик. По профессии юрист.
В 1591 ввёл
Историческая справка
Слайд 7Габриэ́ль Кра́мер
(31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)
Историческая справка
Слайд 8Общий вид системы двух линейных уравнений с двумя переменными x и
Решение системы – это пара чисел (x; y), при подстановке которых каждое уравнение превращается в верное равенство.
Системы двух линейных уравнений
с двумя переменными.
Основные понятия.
Слайд 10 графический метод;
метод подстановки;
метод алгебраического сложения
Методы решения систем двух
Слайд 11Графический метод решения систем, как и графический метод решения уравнений, красив,
Даже если графики уравнений удалось построить, точки пересечения могут быть не такими ‘’хорошими’’, как в специально подобранных примерах учебника, а то и вовсе могут оказаться за пределами чертежа.
Графический метод
Слайд 12В уравнениях системы выразить y через x так, чтобы получить функции.
Найти координаты точек пересечения графиков.
Выписать ответы пары чисел, которые служат координатами точек пересечения графиков.
Алгоритм
решения системы двух уравнений с двумя переменными графическим методом
Слайд 132
Решение:
В уравнениях системы выразить y через x:
а) Построим график уравнения y
б) Построим график уравнения y = -2x + 4. Это прямая, проходящая через точки (0;4) и (2;0).
Пример 1:
Решить графически систему:
y
x
2
1
4
0
3x - y -1= 0
2x + y – 4 = 0
-1
Слайд 142
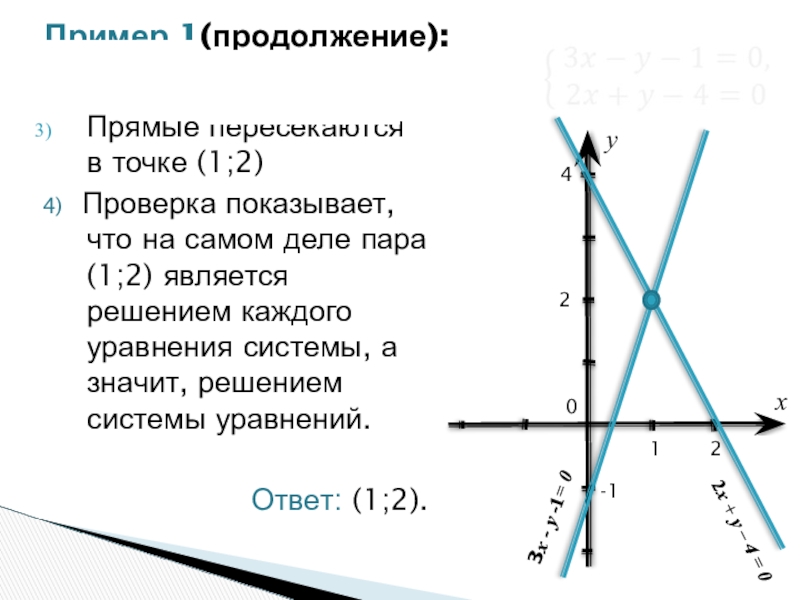
Прямые пересекаются в точке (1;2)
4) Проверка показывает, что на самом деле
Ответ: (1;2).
Пример 1(продолжение):
y
x
2
1
4
0
3x - y -1= 0
2x + y – 4 = 0
-1
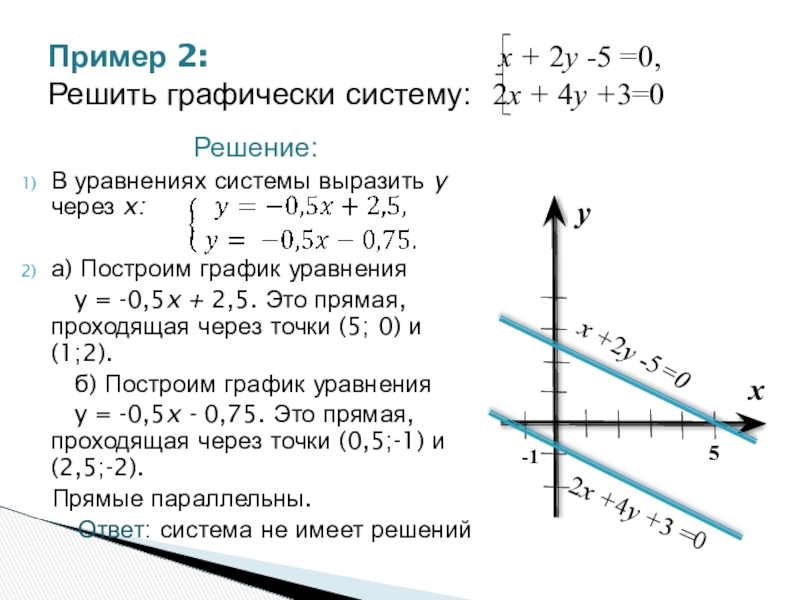
Слайд 15Решение:
В уравнениях системы выразить y через x:
а) Построим график уравнения
y = -0,5x + 2,5. Это прямая, проходящая через точки (5; 0) и (1;2).
б) Построим график уравнения
y = -0,5x - 0,75. Это прямая, проходящая через точки (0,5;-1) и (2,5;-2).
Прямые параллельны.
Ответ: система не имеет решений
Пример 2: x + 2y -5 =0,
Решить графически систему: 2x + 4y +3=0
y
x
5
-1
x +2y -5=0
2x +4y +3 =0
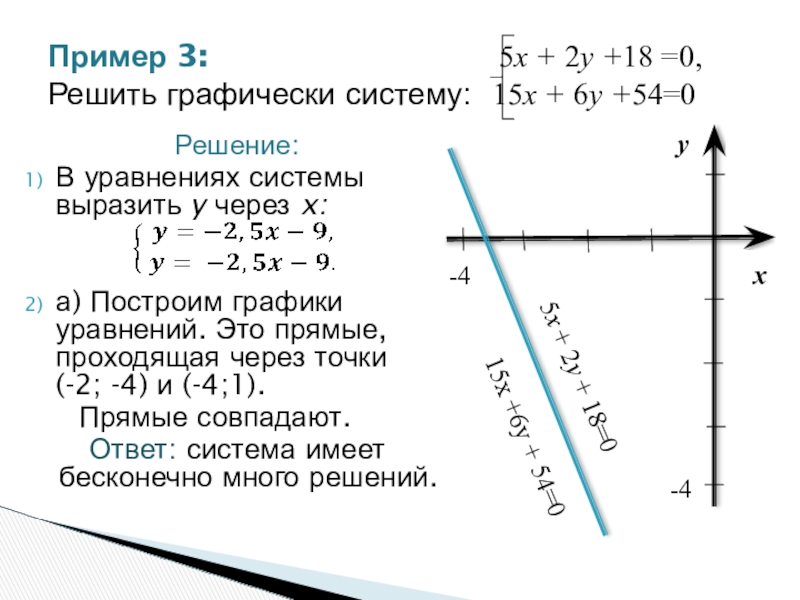
Слайд 16Решение:
В уравнениях системы выразить y через x:
а) Построим графики уравнений. Это
Прямые совпадают.
Ответ: система имеет бесконечно много решений.
Пример 3: 5x + 2y +18 =0,
Решить графически систему: 15x + 6y +54=0
y
x
-4
-4
5x + 2y + 18=0
15x +6y + 54=0
Слайд 19
Метод постановки – это универсальный алгебраический метод. Им можно решать почти
Этот метод может быть не всегда эффективен (т.е. не всегда быстро приводит к цели), но достаточно надёжен.
Метод подстановки
Слайд 20Выразить y через x из первого уравнения системы;
Подставить полученное на первом
Решить полученное на втором шаге уравнение относительно x.
Подставить найденное на третьем шаге значение x в выражении y через x, полученное на первом шаге;
Записать ответ в виде пары значений (x;y), которые были найдены соответственно на третьем и четвёртом шагах.
Алгоритм решения системы двух уравнений
с двумя переменными методом подстановки:
Слайд 21Решение:
Выразим x через y из второго уравнения:
Подставим найденное выражение вместо x в первое уравнение системы: 4 · - 5y =1
Решим полученное уравнение:
6y + 4 – 5y=1,
y +4=1,
y= - 3.
Пример 5: Решить систему методом подстановки:
Слайд 224) Подставим найденное значение y в формулу
x =
5) Пара x = -3,5, y = -3 – единственное решение заданной системы.
Ответ: (-3,5; -3).
Пример 5(продолжение):
Слайд 23Систему уравнений легче решать методом сложения, когда коэффициенты при x и
Метод позволяет быстро исключить одну из неизвестных переменных и найти другую.
.
Метод алгебраического сложения
Слайд 24Преобразовать коэффициенты так, чтобы коэффициенты при x или при y были
Сложить уравнения.
Решить уравнения с одной переменной.
Найти y, подставляя х в одно из первоначальных уравнений.
Записать ответ в виде пары значений (x;y).
Алгоритм решения системы двух уравнений
с двумя переменными методом сложения:
Слайд 25
Решение:
Умножив первое уравнение на 5, а второе на 2, получим коэффициенты
Сложим получившиеся уравнения.
25x + 8x +10y -10y = -45 + 12,
Пример 8: Решить систему методом алгебраического сложения:
Слайд 263) Решим полученное уравнение.
25x + 8x = -45 + 12,
33x =
x = -1
4) Найдём y, подставляя х в одно из первоначальных уравнений:
5 · (-1) + 2y = -9,
2y = -4,
y = -2
5) Пара x = -1, y = -2- решение заданного уравнения.
Ответ: (-1; -2)
Пример 8(продолжение):
Слайд 281) Если главный определитель ∆≠ 0, то система имеет единственное решение
2) Если ∆=0 и хотя бы один из вспомогательных определителей не равен нулю, то система не имеет решений (прямые параллельны, но не совпадают).
3) В случае система сводится к одному линейному уравнению с двумя неизвестными и имеет бесчисленное множество решений (прямые совпадают).
Правило Крамера
Слайд 29Решение:
Найдём определители системы:
=2·(-5) - 3·7= -31
= =8·(-5) – 3·(- 3) = -31
= = 2·(-3) -8·7 = -62
, следовательно система имеет единственное решение: x= =1, y= =2.
Ответ: (1; 2).
Пример 9: Решить уравнение с помощью правила Крамера:
Слайд 30Решение:
Найдём определители системы:
∆ = =2·4 – 3·
= =8· 6 – 3· 10=18≠0.
Ответ: система не имеет решений.
Пример 10: Решить уравнение с помощью правила Крамера:
Слайд 31Решение:
Найдём определители системы:
∆= =2·6 – 3·4 =
= = 8· 6 – 3·16 =0,
= = 2· 16 – 8·4 = 0.
Ответ: система имеет бесконечно много решений.
Пример 11: Решить уравнение с помощью правила Крамера:
Слайд 32Параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу.
Системы линейных уравнений
с параметрами.
Слайд 34Дана система уравнений
Известно, что пара чисел (2;-1) является её решением. Найти
Решение:
Зная, что решением системы являются координаты точки (2; -1), подставляем x = 2, y= -1
№13.17(а)
Слайд 35Сложим получившиеся уравнения:
2a +2a -1b + 1b= 36 + 8
4a =
a=11
Найдём b, подставляя a в одно из первоначальных уравнений:
2 · 11-1b = 36
22- b = 36
b= 22 – 36
b = -14
Ответ: a=11, b = -14
№13.17(а) (продолжение)
Слайд 36Если а =0, то имеем уравнение 0·х = b. Тогда, если,
Если а ≠ 0, то уравнение имеет единственное решение х = .
Схема исследования линейного уравнения с параметрами:
.
Слайд 37Решение: Из второго уравнения найдём х=1–аy и подставим в первое
a(1 – аy) - 3аy = 2а + 3
-a(a + 3) y = a + 3
Исследуем это линейное уравнение.
Возможны случаи:
1) a=0. Тогда уравнение имеет вид:
0·(0+3) y = 0 + 3
0· y = 3
Нет корней. Следовательно, при a=0 система не имеет решений.
Пример 13: Для всех значений параметра а решить систему уравнений
Слайд 382) a= -3. Тогда 3(-3 + 3) y = -3 +3
Следовательно, y – любое число. При этом
x = 1 – аy = 1 –(-3) y = 1+ 3y
3) a ≠ 0, a ≠ -3.
Тогда из уравнения -a(a + 3) y = a + 3 выразим y:
y = = - ,
а полученное значение y подставим во второе уравнение: x = 1 – аy = 1 – a(- ) = 2.
Ответ: если a=0, то система не имеет решений;
если a= -3, то x = 1+ 3y, y – любое число;
если a ≠ 0, a ≠ -3, то x = 2, y = -
Пример 13(продолжение):
Слайд 39Решение: Найдём определители системы:
∆ =
= (3а + 2)(5а + 6) - (2а + 3)(2а + 4) = = а(11а + 14)
= (а + 5)(2а + 4) - (3а + 2)(3а + 10) =
= -а(7а + 22)
Пример 14: Для всех значений параметра а решить систему уравнений:
Слайд 40∆ = а(2 - а) ≠ 0 а ≠
x = = =
y = = - = - =
2) ∆ = а(2 - а) = 0, тогда а = 0 или а = 2.
При а = 0 определители
= а(11а + 14) = 0·(11·0 + 14) = 0,
= - а(7а + 22) = - 0·(7·0 + 22) = 0,
0. Тогда система имеет вид
5x + 3y = 2 x – произвольное число
Пример14(продолжение):
Слайд 41б) при а = 2 определитель
а(11а + 14) =
Этого достаточно, чтобы утверждать, что система не имеет решений.
Ответ: если а ≠ 0 и а ≠ 2, то x = , y = ;
если а = 0, то x – любое число, y = - x;
если а = 2, то система не имеет решений.
Пример14(продолжение):
Слайд 42Алгебра: Учеб. Для 7 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г.
Выготский М.Я. Справочник по высшей математике. 10-е изд., стереотипное.- М.: Издательство «Наука», главная редакция физико-математической литературы, 1973.- 872с.
Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. 3-е издание, дополненное и переработанное.- М.: Илекса, Харьков: Гимназия, 1999. – 336с.
Кузнецова Л.В., Суворова С.Б. и др. Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2009/ФИПИ.- М.: Интеллект-Центр, 2009.
Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: СИ. Адян, Н.С Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988.- 847 с, ил.
Мордкович А.Г. Алгебра. 7 кл.: В двух частях.- 9-е изд.- М.: Мнемозина, 2010.
Мочалов В.В., Сильвестров В.В. Уравнения и неравенства с параметрами: Учебное пособие.- 2-е изд., доп., перераб.- Чебоксары: изд-во Чуваш. ун-та, 2000. – 144с.
Литература: