образования № 80
Центральный район
Санкт-Петербург
2016
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре. Математическая игра 10 000 000 Решение задач КИМ ГИА.
Содержание
- 1. Презентация по алгебре. Математическая игра 10 000 000 Решение задач КИМ ГИА.
- 2. Правила игры:Учащиеся делятся на две команды. Выбирают
- 3. ковалевская Софья васильевна (1850-1891)
- 4. капитаны команд.
- 5. 1 заданиеНа счету Машиного мобильного телефона было
- 6. ВАРИАНТЫ ОТВЕТА
- 7. Правильный ответ (З-1)Решение. Разговор с Леной стоил Маше 53 − 8 = 45 рублей. Разделим 45 на 2,5: ответ:18
- 8. 2 заданиеНа рисунке жирными точками показана среднесуточная
- 9. ВАРИАНТЫ ОТВЕТА
- 10. ПРАВИЛЬНЫЙ ОТВЕТ (З-2)Решение. Из графика видно, что
- 11. 3 заданиеНайдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1.
- 12. ВАРИАНТЫ ОТВЕТА
- 13. ПРАВИЛЬНЫЙ ОТВЕТ (З-3)Решение. Площадь квадрата равна разности
- 14. 4 заданиеСвоему постоянному клиенту компания сотовой связи
- 15. ВАРИАНТЫ ОТВЕТА
- 16. ПРАВИЛЬНЫЙ ОТВЕТ (З-4)Решение. Рассмотрим различные варианты.
- 17. 5 заданиеРешите уравнение . В ответе напишите наибольший отрицательный корень.
- 18. ВАРИАНТЫ ОТВЕТА
- 19. ПРАВИЛЬНЫЙ ОТВЕТ (З-5) Решение. Решим уравнение:
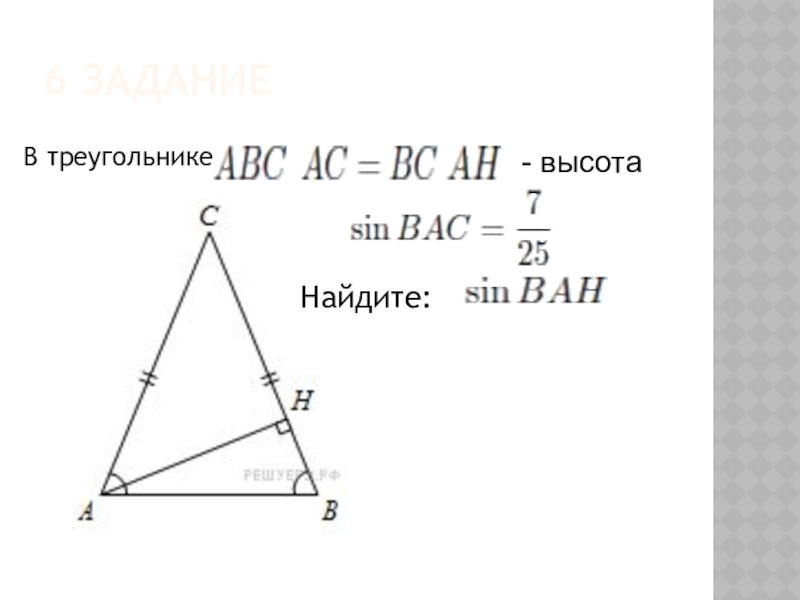
- 20. 6 задание В треугольнике - высота Найдите:
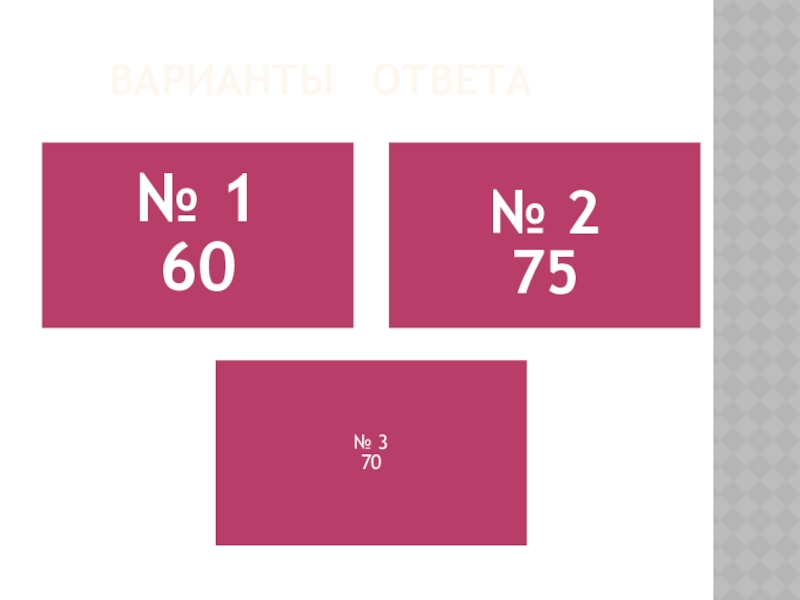
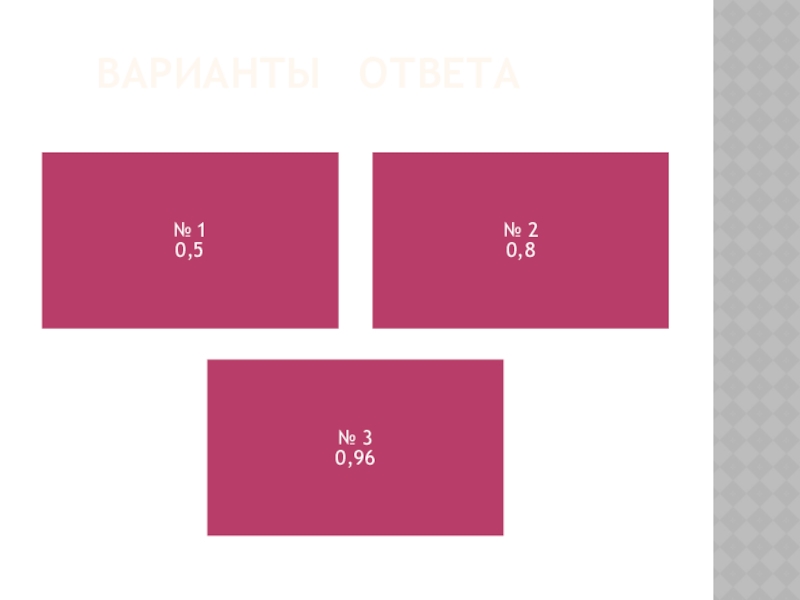
- 21. ВАРИАНТЫ ОТВЕТА
- 22. ПРАВИЛЬНЫЙ ОТВЕТ (З-6)Решение. Треугольник равнобедренный, значит, углы равны как углы при его основании.Ответ: 0,96.
- 23. 7 ЗАДАНИЕНайдите: если
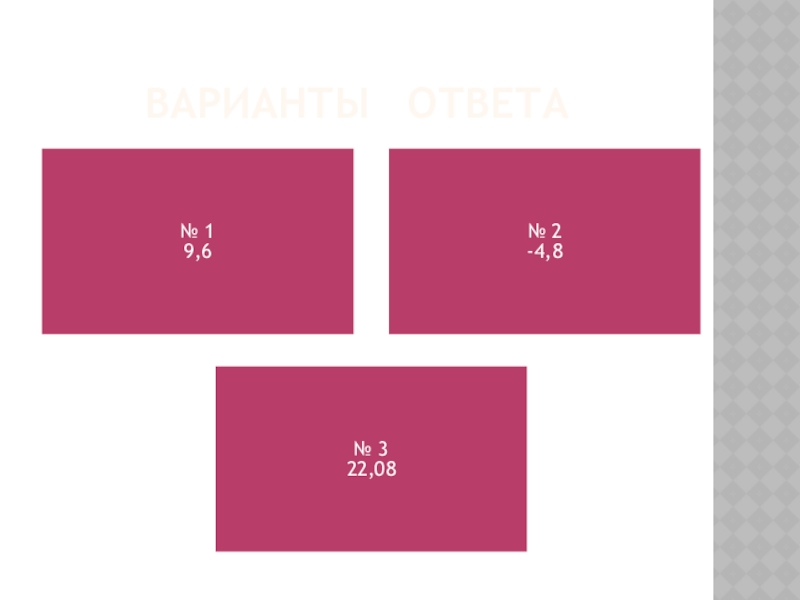
- 24. ВАРИАНТЫ ОТВЕТА
- 25. ПрАВИЛЬНЫЙ ОТВЕТ (З-7)Решение. Используем формулу косинуса
- 26. 8 заданиеМатериальная точка движется прямолинейно по закону
- 27. ВАРИАНТЫ ОТВЕТА
- 28. ПРАВИЛЬНЫЙ ОТВЕТ (З-8)Решение. Найдем производную (закон изменения скорости):При t = 9 c имеем: Ответ: 60.
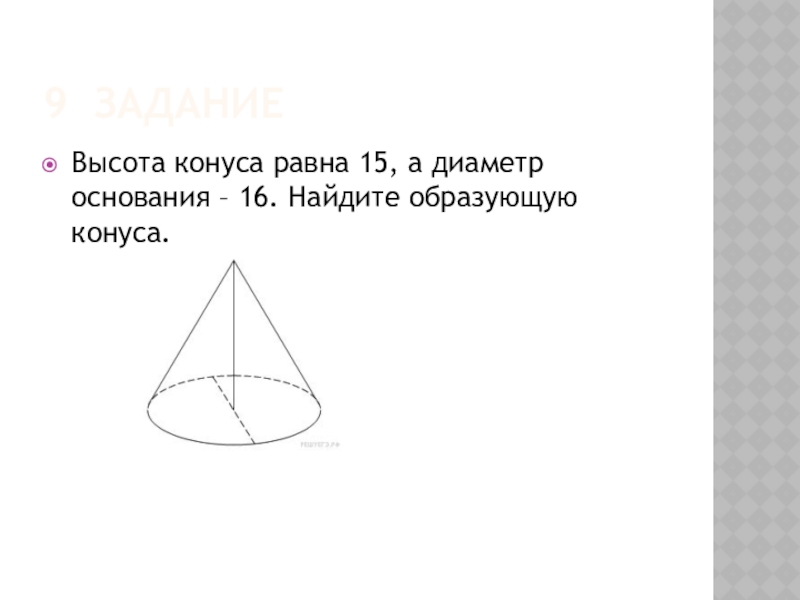
- 29. 9 заданиеВысота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса.
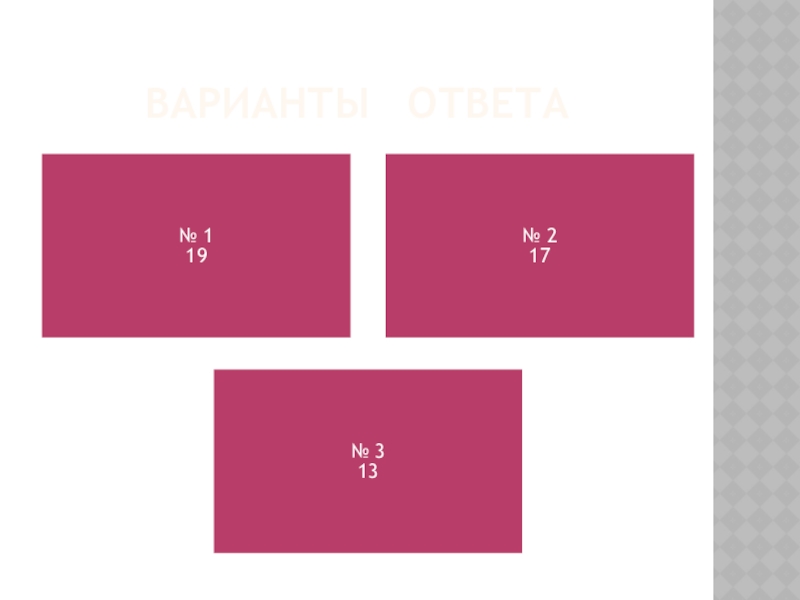
- 30. ВАРИАНТЫ ОТВЕТА
- 31. ПРАВИЛЬНЫЙ ОТВЕТ (З-9)Решение. образующая конуса по теореме Пифагора равна Ответ: 17.
- 32. 10 заданиеМаша включает телевизор. Телевизор включается на
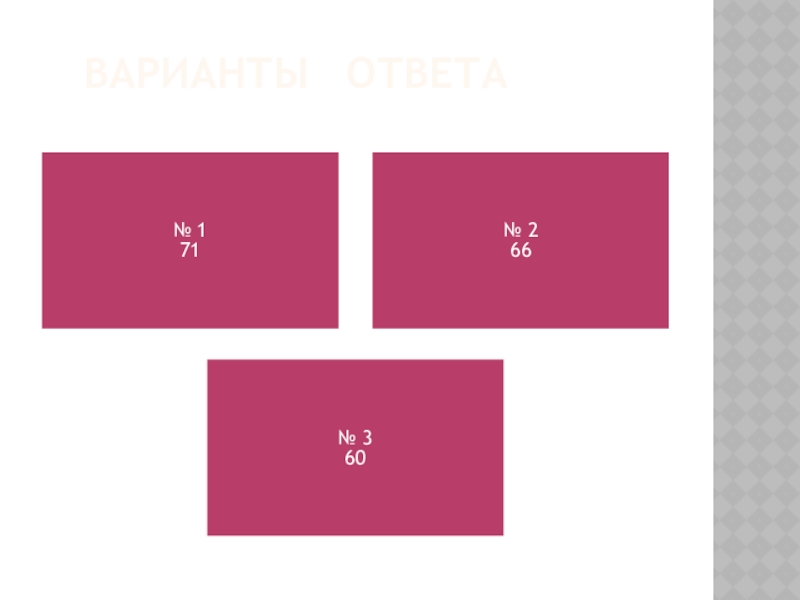
- 33. ВАРИАНТЫ ОТВЕТА
- 34. ПРАВИЛЬНЫЙ ОТВЕТ (З-10)Решение. новости не идут по
- 35. 11 заданиеДва ребра прямоугольного параллелепипеда, выходящие из
- 36. ВАРИАНТЫ ОТВЕТА
- 37. ПРАВИЛЬНЫЙ ОТВЕТ (З-11)Обозначим известные ребра за a1
- 38. 12 задание Некоторая компания продает свою
- 39. ВАРИАНТЫ ОТВЕТА
- 40. ПРАВИЛНЫЙ ОТВЕТ (З-12)Решение. Задача сводится к нахождению
- 41. 13 заданиеДвое рабочих, работая вместе, могут выполнить
- 42. ВАРИАНТЫ ОТВЕТА
- 43. ПРАВИЛЬНЫЙ ОТВЕТ (З-13)Решение.Обозначим и
- 44. 14 задание. Найдите наименьшее значение функциина отрезке
- 45. ВАРИАНТЫ ОТВЕТА
- 46. ПРАВИЛЬНЫЙ ОТВЕТ (З-14)Решение. Найдем производную заданной
- 47. Подведение итогов игры. НАГРАЖДЕНИЕ ПОБЕДИТЕЛЕЙ.
- 48. Победители игры «10 000 000»
Правила игры:Учащиеся делятся на две команды. Выбирают капитанов, дают команде название, придумывают девиз. Каждая команда получает по 10 000 000 «алгиом» - условных денежных единиц. В процессе игры вызываются пары участников: либо по желанию самих игроков, либо по
Слайд 2Правила игры:
Учащиеся делятся на две команды. Выбирают капитанов, дают команде название,
придумывают девиз. Каждая команда получает по 10 000 000 «алгиом» - условных денежных единиц. В процессе игры вызываются пары участников: либо по желанию самих игроков, либо по решению капитанов команд. Игроки должны решить задание-тест, к которому дано три ответ, и указать правильный ответ. Кроме этого игроки должны поместить разыгрываемые суммы на номер правильного ответа, а если не уверенны в его правильности, то на другие два номера или на один, по своему усмотрению. Сумму, поставленную на проигравший номер, игроки теряют. Таким образом, подростки испытывают ответственность за свои примененные знания и принятые решения. Если в процессе игры, они теряют все средства, но имеют желание отыграться, то им «предоставляется кредит». Или, потерявшей все средства, команде присуждается поражение, а другой команде – победа. Участников игры и победителей ждут призы и подарки.
Слайд 51 задание
На счету Машиного мобильного телефона было 53 рубля, а после
разговора с Леной осталось 8 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 2 рубля 50 копеек?
Слайд 7Правильный ответ (З-1)
Решение.
Разговор с Леной стоил Маше 53 − 8 = 45 рублей. Разделим 45
на 2,5:
ответ:18
ответ:18
Слайд 82 задание
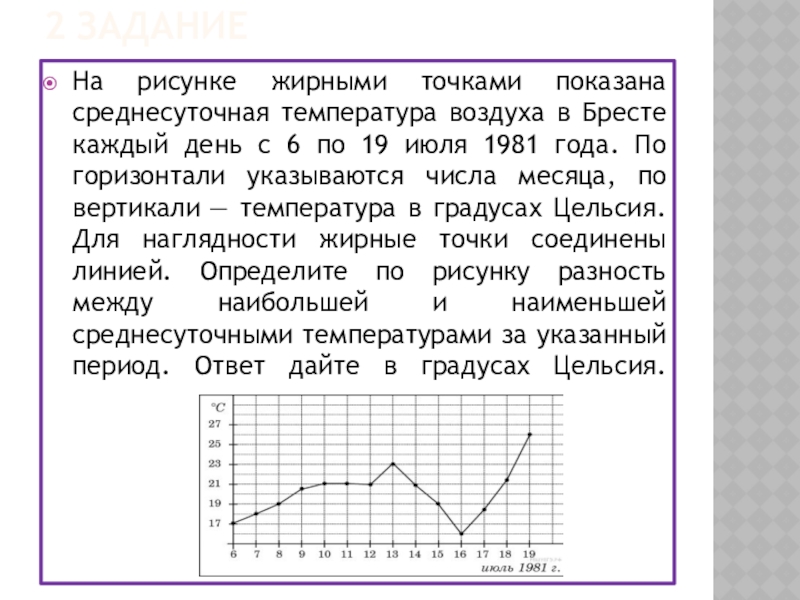
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте
каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.
Слайд 10ПРАВИЛЬНЫЙ ОТВЕТ (З-2)
Решение.
Из графика видно, что наибольшая и наименьшая температура за
указанный период составляла
26 °C и 16 °C
соответственно.
Их разность равняется 10 °C.
ответ: 10
ответ: 10
Слайд 13ПРАВИЛЬНЫЙ ОТВЕТ (З-3)
Решение.
Площадь квадрата равна разности площади прямоугольника и четырех равных
прямоугольных треугольников, гипотенузы которых являются сторонами исходного квадрата. Поэтому
Ответ: 10.
Ответ: 10.
Слайд 144 задание
Своему постоянному клиенту компания сотовой связи решила предоставить на выбор
одну из скидок. Либо скидку 25% на звонки абонентам других сотовых компаний в своем регионе, либо скидку 5% на звонки в другие регионы, либо 15% на услуги мобильного интернета. Клиент посмотрел распечатку своих звонков и выяснил, что за месяц он потратил 300 рублей на звонки абонентам других компаний в своем регионе, 200 рублей на звонки в другие регионы и 400 рублей на мобильный интернет. Клиент предполагает, что в следующем месяце затраты будут такими же, и, исходя из этого, выбирает наиболее выгодную для себя скидку. Какую скидку выбрал клиент? В ответ запишите, сколько рублей составит эта скидка.
Слайд 16ПРАВИЛЬНЫЙ ОТВЕТ (З-4)
Решение.
Рассмотрим различные варианты.
Скидка звонки абонентам других компаний в
своем регионе составит 0,25 300 = 75 руб.
Скидка на звонки в другие регионы составит 0,05 200 = 10 руб.
Скидка на мобильный Интернет составит 0,15 400 = 60 руб.
Ответ: 75.
Ответ: 75.
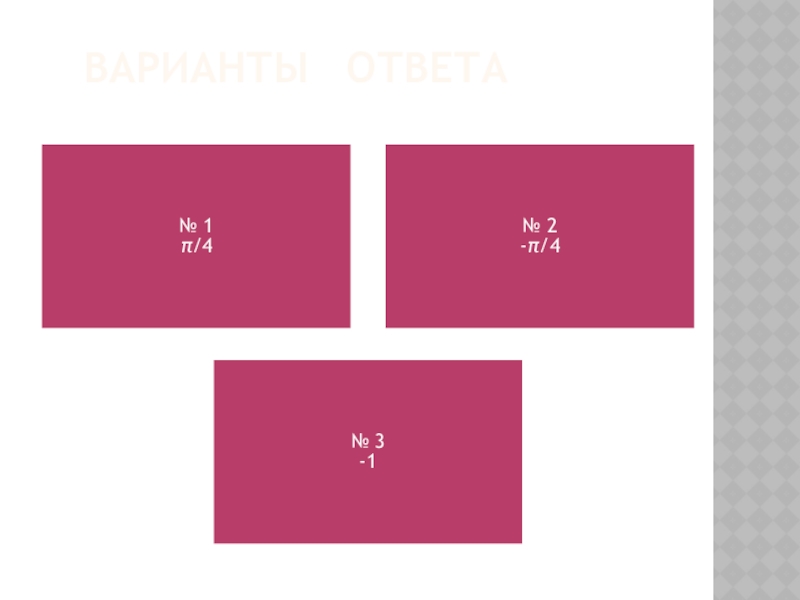
Слайд 19ПРАВИЛЬНЫЙ ОТВЕТ (З-5)
Решение.
Решим уравнение:
Положительным значениям параметра соответствуют положительные значения корней,
отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
Ответ: −1.
Ответ: −1.
Слайд 22ПРАВИЛЬНЫЙ ОТВЕТ (З-6)
Решение.
Треугольник равнобедренный, значит, углы равны как углы при его
основании.
Ответ: 0,96.
Ответ: 0,96.
Слайд 25ПрАВИЛЬНЫЙ ОТВЕТ (З-7)
Решение.
Используем формулу косинуса двойного угла COS 2x
= 1- 2 sin²x
Ответ: 22,08.
Ответ: 22,08.
Слайд 268 задание
Материальная точка движется прямолинейно по закону (где x — расстояние от
точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
Закон движения:
Слайд 28ПРАВИЛЬНЫЙ ОТВЕТ (З-8)
Решение.
Найдем производную (закон изменения скорости):
При t = 9 c
имеем:
Ответ: 60.
Ответ: 60.
Слайд 3210 задание
Маша включает телевизор. Телевизор включается на случайном канале. В это
время по девяти каналам из сорока пяти показывают новости. Найдите вероятность того, что Маша попадет на канал, где новости не идут.
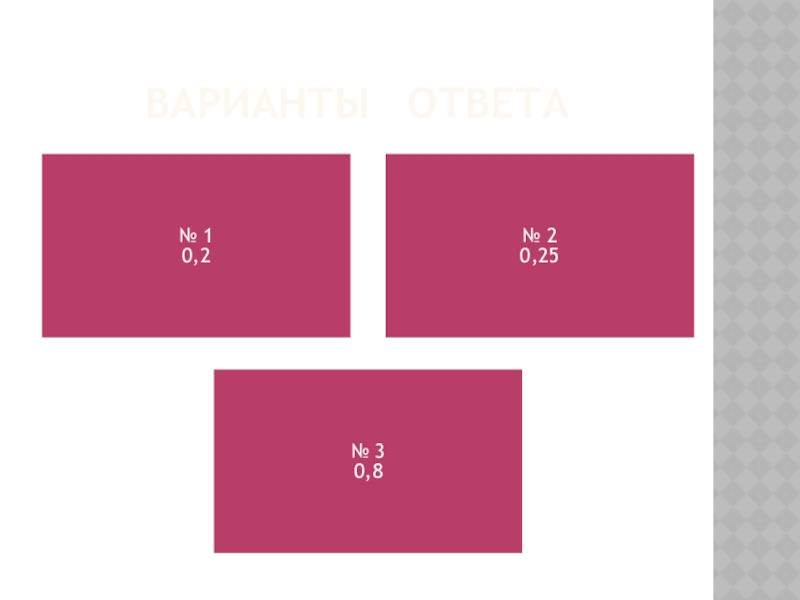
Слайд 34ПРАВИЛЬНЫЙ ОТВЕТ (З-10)
Решение.
новости не идут по 45 – 9 = 36 каналам. Тогда вероятность того,
что Маша попадет на канал где новости не идут, равна
Ответ: 0,8.
Ответ: 0,8.
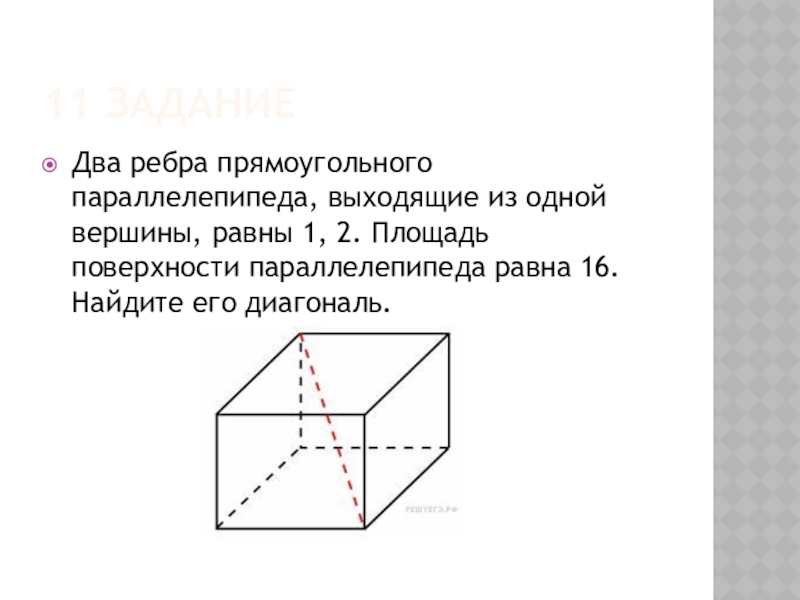
Слайд 3511 задание
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1,
2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
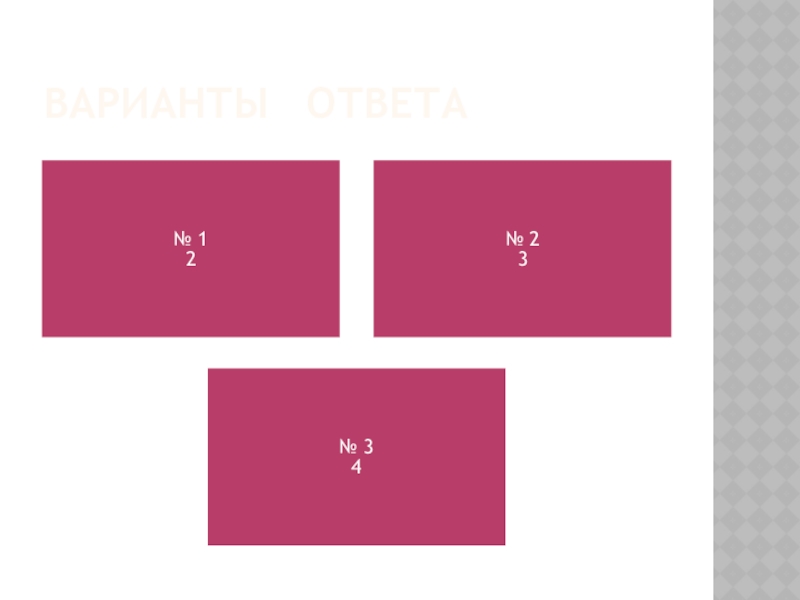
Слайд 37ПРАВИЛЬНЫЙ ОТВЕТ (З-11)
Обозначим известные ребра за a1 и a2, а неизвестное
за a3. Площадь поверхности параллелепипеда выражается как
Выразим a3
Диагональ параллелепипеда находится как Ответ: 3.
Выразим a3
Диагональ параллелепипеда находится как Ответ: 3.
(З-1)
Слайд 3812 задание
Некоторая компания продает свою продукцию по цене
руб. за единицу, переменные затраты на производство одной единицы продукции составляют руб., постоянные расходы предприятия руб. месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле
Определите наименьший месячный объeм производства (единиц продукции) , при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.
Определите наименьший месячный объeм производства (единиц продукции) , при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.
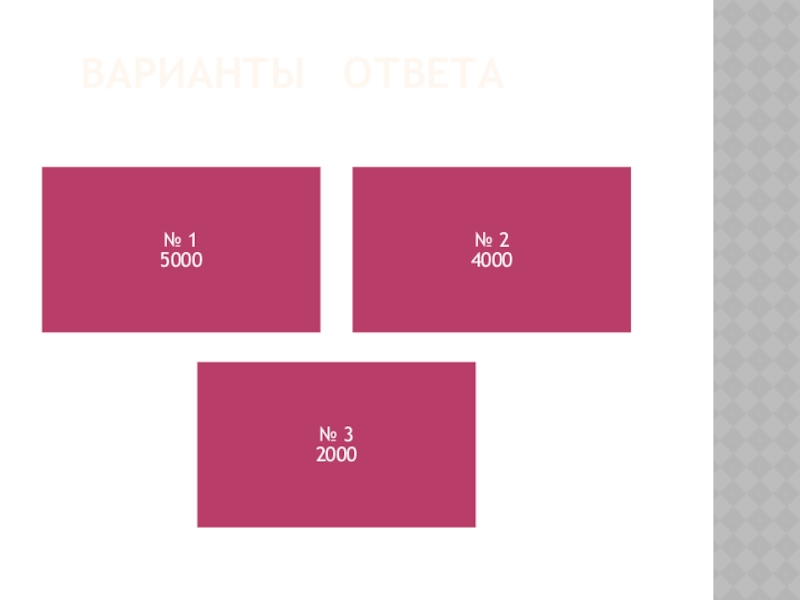
Слайд 40ПРАВИЛНЫЙ ОТВЕТ (З-12)
Решение.
Задача сводится к нахождению наименьшего решения неравенства
при
заданных значениях цены за единицу
, переменных затрат на производство одной единицы продукции и постоянных расходов предприятия в месяц:
Ответ: 5000.
, переменных затрат на производство одной единицы продукции и постоянных расходов предприятия в месяц:
Ответ: 5000.
Слайд 4113 задание
Двое рабочих, работая вместе, могут выполнить работу за 12 дней.
За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?
Слайд 43ПРАВИЛЬНЫЙ ОТВЕТ (З-13)
Решение.Обозначим и –
объёмы работ, которые выполняют за день первый и второй рабочий, соответственно, полный объём работ примем за 1.
Тогда по условию задачи и
. Решим полученную систему:
Тем самым, первый рабочий за день выполняет одну двадцатую всей работы, значит, работая отдельно, он справится с ней за 20 дней. Ответ: 20.
Тогда по условию задачи и
. Решим полученную систему:
Тем самым, первый рабочий за день выполняет одну двадцатую всей работы, значит, работая отдельно, он справится с ней за 20 дней. Ответ: 20.
Слайд 46ПРАВИЛЬНЫЙ ОТВЕТ (З-14)
Решение. Найдем производную заданной функции:
Найдем нули
производной на заданном
отрезке:
В точке заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
Ответ: 12.
В точке заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
Ответ: 12.