- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Квадратные неравенства (9 класс)
Содержание
- 1. Презентация по алгебре Квадратные неравенства (9 класс)
- 2. Инструкционная карта Решение квадратных неравенств ах2
- 3. 4. Если уравнение имеет корни, то отмечаемкорни
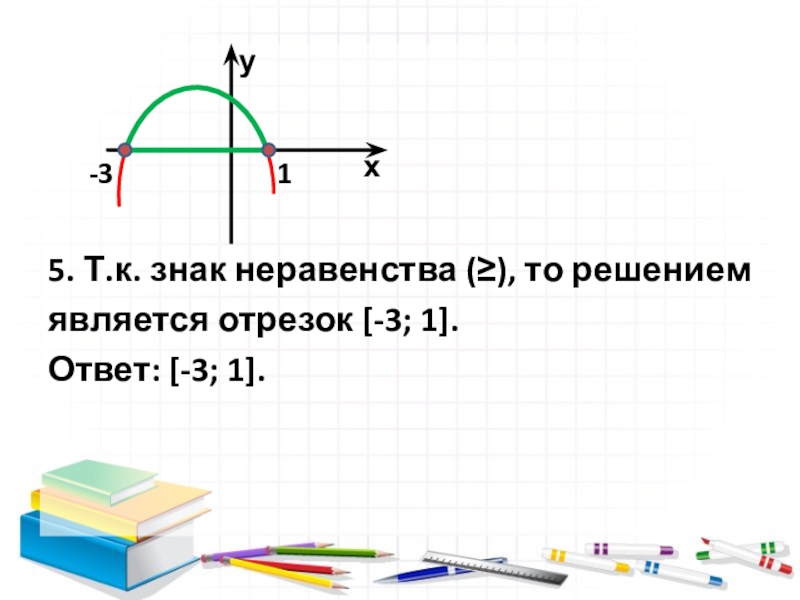
- 4. Пример 1 D 0Решить неравенство -х2 - 2x + 3 0.
- 5. Пример 1 D
- 6. 5. Т.к. знак неравенства (), то решениемявляется отрезок -3; 1.Ответ: -3; 1.-3ух1
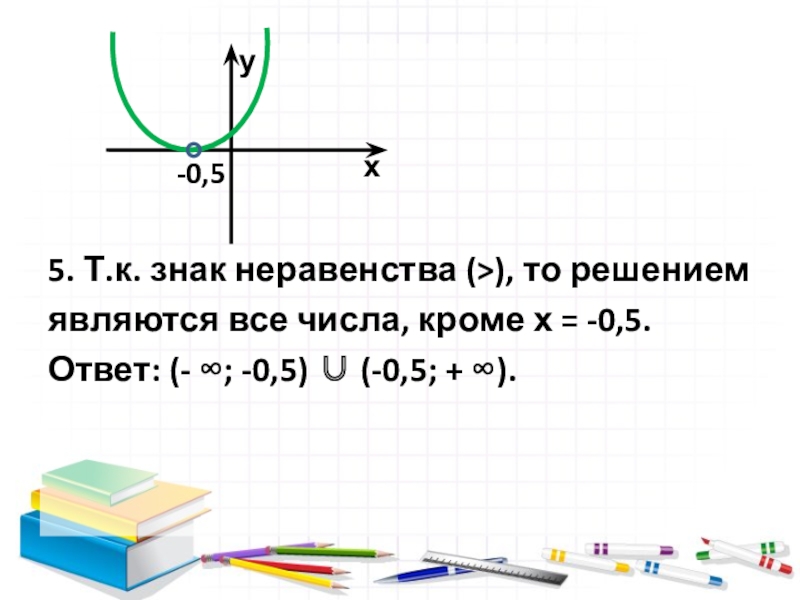
- 7. Пример 2 D = 0Решить неравенство 4х2 + 4x + 1 0.
- 8. Пример 2 D = 0Решить
- 9. 5. Т.к. знак неравенства (), то решениемявляются
- 10. Решением неравенства 4х2 + 4x + 1
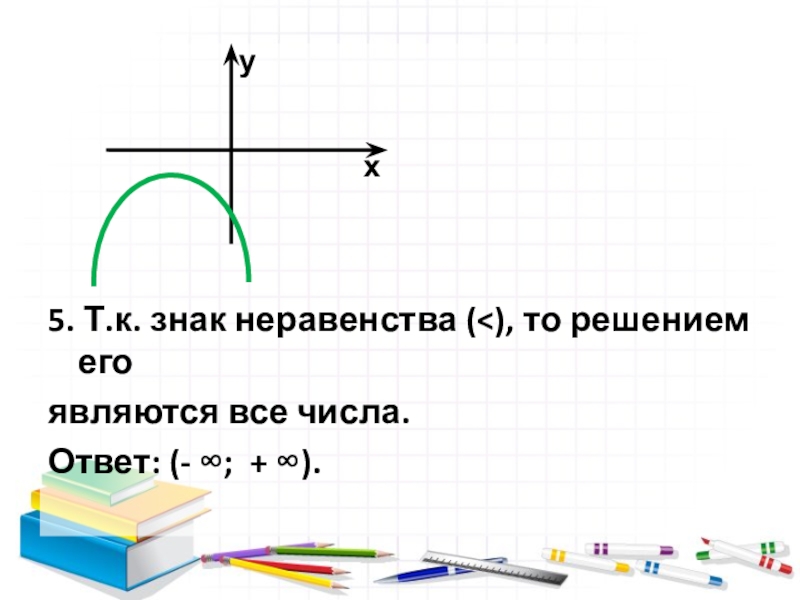
- 11. Пример 3 D 0Решить неравенство -х2 - 6x - 10 0.
- 12. Пример 3 D 0Решить неравенство -х2
- 13. 5. Т.к. знак неравенства (), то решением егоявляются все числа.Ответ: (- ; + ).ух
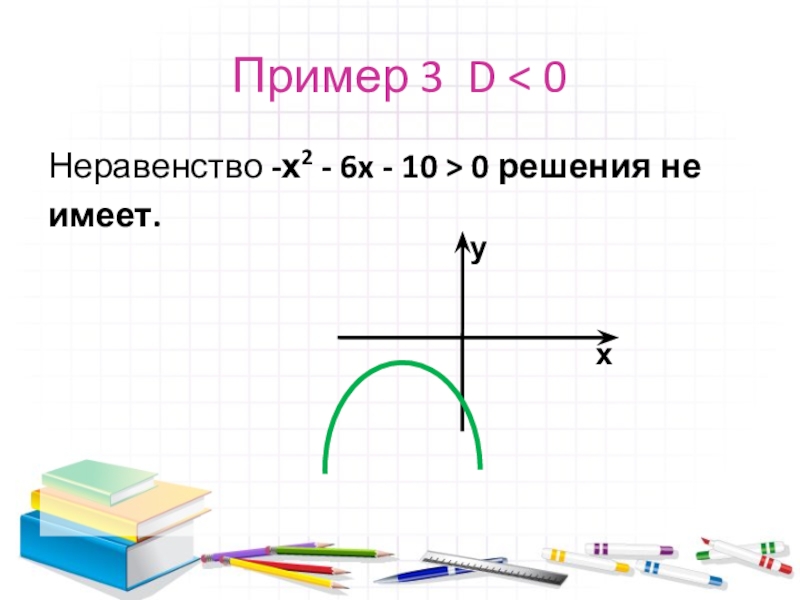
- 14. Пример 3 D 0Неравенство -х2 - 6x - 10 0 решения неимеет.ух
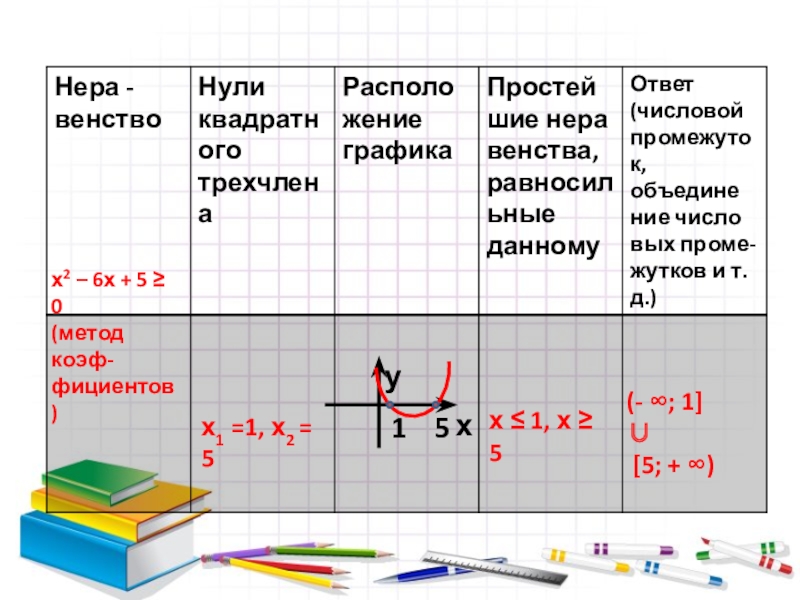
- 15. х2 – 6х + 5 0(метод
Инструкционная карта Решение квадратных неравенств ах2 + bx + с 0 ( 0, 0, 0) 1. Вводим соответствующую функцию у = ах2 + bx + с.2. Определяем направление ветвейпараболы у = ах2
Слайд 2Инструкционная карта Решение квадратных неравенств ах2 + bx + с 0
( 0, 0, 0)
1. Вводим соответствующую функцию
у = ах2 + bx + с.
2. Определяем направление ветвей
параболы у = ах2 + bx + с ( при а 0 ветви
направлены вверх; при а 0 ветви
направлены вниз).
3. Находим нули функции, т.е. решаем
уравнение ах2 + bx + с =о.
Слайд 34. Если уравнение имеет корни, то отмечаем
корни на координатной прямой и
схематически
рисуем параболу в соответствии
с направлением ветвей. Если уравнение не
имеет корней, то схематически рисуем
параболу в соответствии с направлением
ветвей.
5. Находим решение неравенства с учетом
смысла знака неравенства.
с направлением ветвей. Если уравнение не
имеет корней, то схематически рисуем
параболу в соответствии с направлением
ветвей.
5. Находим решение неравенства с учетом
смысла знака неравенства.
Слайд 5Пример 1 D 0
Решить неравенство -х2 -
2x + 3 0.
Пусть у = -х2 - 2x + 3.
а = -1 0, ветви направлены вниз.
Решим уравнение -х2 - 2x + 3 = 0
х = 1 и х = -3.
4. Отметим числа 1 и -3 на координатной
прямой и построим эскиз графика.
Пусть у = -х2 - 2x + 3.
а = -1 0, ветви направлены вниз.
Решим уравнение -х2 - 2x + 3 = 0
х = 1 и х = -3.
4. Отметим числа 1 и -3 на координатной
прямой и построим эскиз графика.
Слайд 8Пример 2 D = 0
Решить неравенство 4х2 + 4x
+ 1 0.
Пусть f(x) = 4х2 + 4x + 1 .
а = 4 0 , ветви направлены вверх.
Решим уравнение 4х2 + 4x + 1 = 0
х1 = х2 = -0,5.
4. Парабола касается оси абсцисс.
Пусть f(x) = 4х2 + 4x + 1 .
а = 4 0 , ветви направлены вверх.
Решим уравнение 4х2 + 4x + 1 = 0
х1 = х2 = -0,5.
4. Парабола касается оси абсцисс.
Слайд 9
5. Т.к. знак неравенства (), то решением
являются все числа, кроме х
= -0,5.
Ответ: (- ; -0,5) (-0,5; + ).
Ответ: (- ; -0,5) (-0,5; + ).
-0,5
у
х
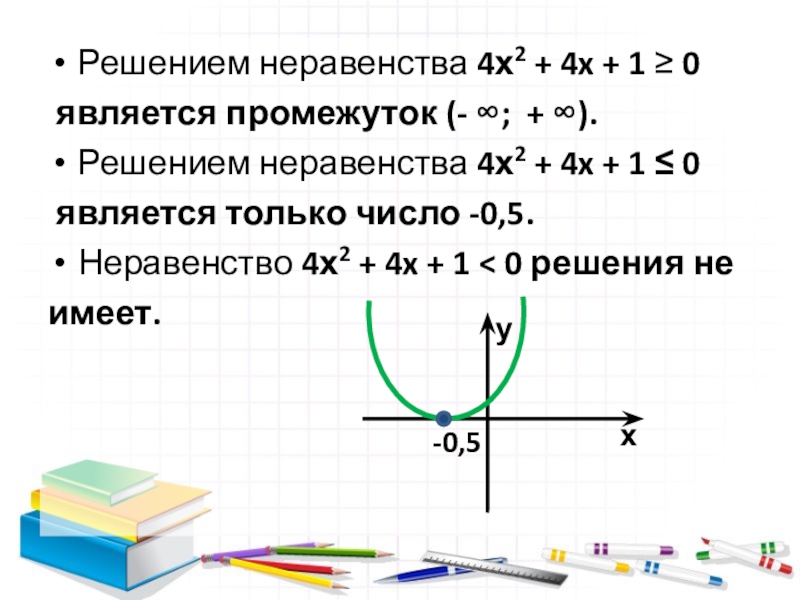
Слайд 10Решением неравенства 4х2 + 4x + 1 0
является промежуток
(- ; + ).
Решением неравенства 4х2 + 4x + 1 0
является только число -0,5.
Неравенство 4х2 + 4x + 1 0 решения не
имеет.
Решением неравенства 4х2 + 4x + 1 0
является только число -0,5.
Неравенство 4х2 + 4x + 1 0 решения не
имеет.
-0,5
у
х
Слайд 12Пример 3 D 0
Решить неравенство -х2 - 6x - 10
0.
Пусть f(x) = -х2 - 6x - 10.
а = -1 0, ветви направлены вниз.
Уравнение -х2 - 6x - 10 = 0 решения не
имеет.
4. Парабола не пересекает ось х и не
касается её.
Пусть f(x) = -х2 - 6x - 10.
а = -1 0, ветви направлены вниз.
Уравнение -х2 - 6x - 10 = 0 решения не
имеет.
4. Парабола не пересекает ось х и не
касается её.