МКОУ СОШ №1 г. Сортавала РК Карелия
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре к уроку по теме Решение рациональных неравенств
Содержание
- 1. Презентация по алгебре к уроку по теме Решение рациональных неравенств
- 2. Метод интервалов заключается в следующем:Числовая прямая разбивается
- 3. Назовите числа, при которых числитель и знаменатель будут равны нулюОтвет: 7; -9 и 5
- 4. Назовите выколотые и закрашенные точкиОтвет: выколотые 15; -8 и -1Ответ: выколотые 15, закрашенные -8 и -1
- 5. Назовите выколотые и закрашенные точкиОтвет: выколотые 5
- 6. Решите неравенство: (х2 - 16)(х + 3) 0
- 7. Решите неравенство:038-++-
- 8. Решите неравенство:(x + 2)2x - 30
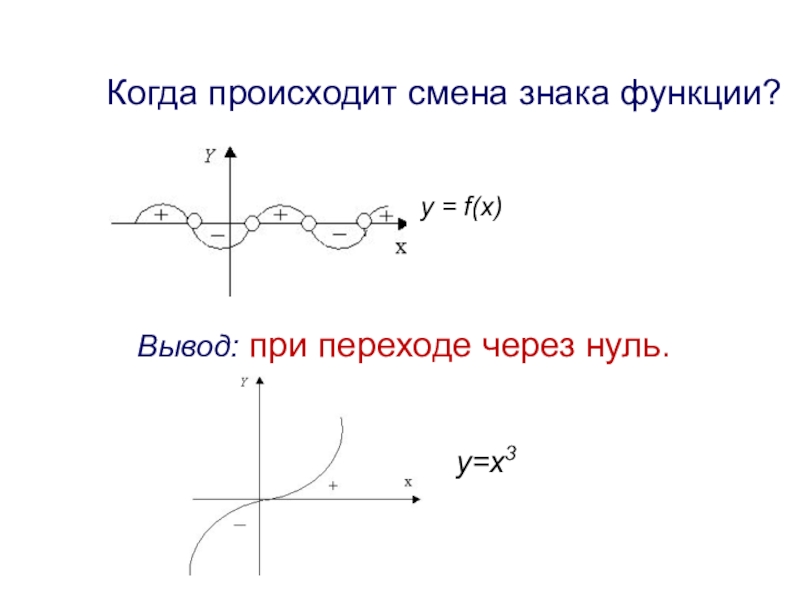
- 9. Когда происходит смена знака функции?y = f(x)Вывод: при переходе через нуль.y=x3
- 10. Обращаем внимание: х=0 не является нулем функции,
- 11. Точка х=0 является нулем функции, но функция
- 12. Решите неравенство:Решений нетВывод: выражение, стоящее в четной
- 13. Решите неравенство:(x + 2)2x - 30
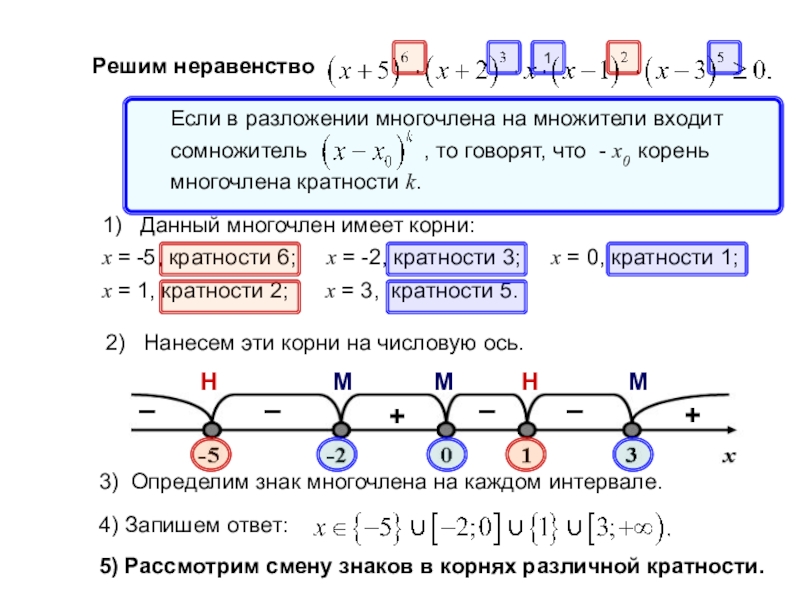
- 14. Решим неравенство1) Данный многочлен имеет корни:
- 15. Обобщая ваши наблюдения, делаем выводы:
- 16. Решите неравенствоИспользуйте полученные выводы о смене знака на интервалах, в зависимости от степени кратности корня.
- 17. Решите неравенство:
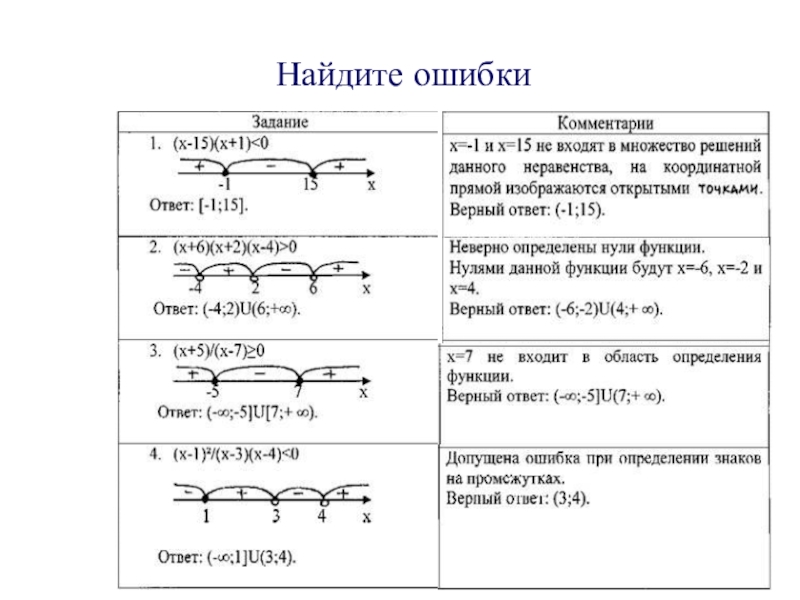
- 18. Найдите ошибки
- 19. Решите неравенство:Вывод: х=-2 – корень четной кратности,
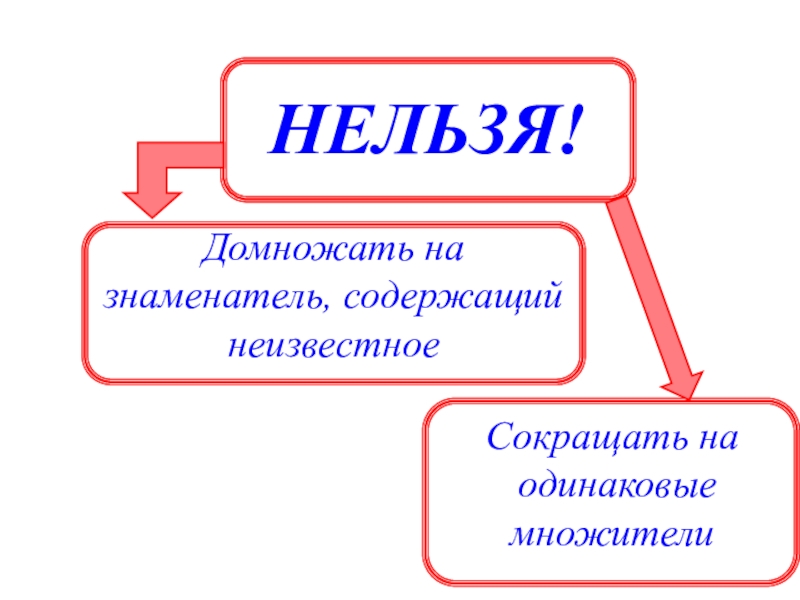
- 20. НЕЛЬЗЯ!Домножать назнаменатель, содержащий неизвестноеСокращать на одинаковыемножители
- 21. Решите неравенство:(x + 1)·(x + 3)(x + 1)·(x + 3)x + 3x + 3˃≥00
- 22. Чтобы определить знак на промежутке, нужно вычислить
- 23. Решить неравенство:Решение:Ответ:
- 24. Решите неравенство
- 25. Решить неравенства:
- 26. Спасибо за работу!Домашнее задание: №22 а,б; №23 а,б
Метод интервалов заключается в следующем:Числовая прямая разбивается нулями функции на конечное число интервалов, на каждом из которых функция сохраняет знак.Чтобы определить этот знак, нужно вычислить значение функции в какой-либо одной точке из каждого такого интервала.
Слайд 1Решение
рациональных неравенств
методом интервалов
урок алгебры в 9 классе
Монахова Е.Ю. –
учитель математики
Слайд 2Метод интервалов заключается в следующем:
Числовая прямая разбивается нулями функции на конечное
число интервалов, на каждом из которых функция сохраняет знак.
Чтобы определить этот знак, нужно вычислить значение функции в какой-либо одной точке из каждого такого интервала.
Слайд 4Назовите выколотые и закрашенные точки
Ответ: выколотые 15; -8 и -1
Ответ: выколотые
15, закрашенные -8 и -1
Слайд 10Обращаем внимание: х=0 не является нулем функции, но при переходе через
нуль знак функции меняется.
Вывод: точки, которые обращают в нуль знаменатель (точки разрыва) тоже должны быть учтены как точки, при переходе через которые функция меняет свой знак.
Слайд 11Точка х=0 является нулем функции, но функция при переходе через нуль
знак не меняет
y=x2
Вывод: y=x2 относится к категории особых случаев, так как четная степень функции не влияет на знак неравенства, перемены знака не происходит
Слайд 12Решите неравенство:
Решений нет
Вывод: выражение, стоящее в четной степени, не влияет на
знак неравенства, но влияет на решение и отбрасывать его без дополнительных ограничений нельзя
Слайд 14
Решим неравенство
1) Данный многочлен имеет корни:
x = -5, кратности
6; x = -2, кратности 3; x = 0, кратности 1;
x = 1, кратности 2; x = 3, кратности 5.
x = 1, кратности 2; x = 3, кратности 5.
2) Нанесем эти корни на числовую ось.
3) Определим знак многочлена на каждом интервале.
+
+
–
–
–
–
4) Запишем ответ:
5) Рассмотрим смену знаков в корнях различной кратности.
М
Н
Н
М
М
Слайд 16
Решите неравенство
Используйте полученные выводы о смене знака на интервалах, в зависимости
от степени кратности корня.
Слайд 19Решите неравенство:
Вывод: х=-2 – корень четной кратности, при переходе через который
функция знак не меняет .
Выражение, которое можно сократить – это тоже особый случай
Слайд 22Чтобы определить знак на промежутке, нужно вычислить значение функции в какой-либо
одной точке из каждого такого интервала.
Можно упростить, если оговорить понятие особых случаев, которые влияют на знак интервала.
Особые случаи:
Линейный множитель стоит в четной степени.
Выражение, которое можно сократить.
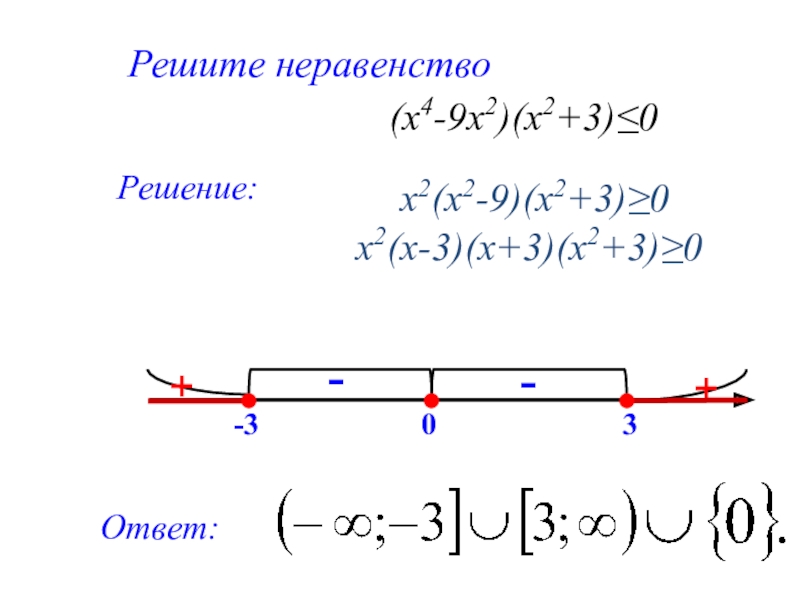
Слайд 24 Решите неравенство
(х4-9х2)(х2+3)≤0
Решение:
х2(х2-9)(х2+3)≥0
х2(х-3)(х+3)(х2+3)≥0
-3
0
3
+
+
-
-
Ответ:
