- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Использование ИКТ при изучении квадратичной функции
Содержание
- 1. Презентация по алгебре Использование ИКТ при изучении квадратичной функции
- 2. использование компьютерных технологий:- для построения графиков -
- 3. История развития понятия функции4-5 тыс лет назад
- 4. Слайд 4
- 5. Применение квадратичной функции в жизни
- 6. Есть любопытное свойство параболы. Пусть
- 7. Слайд 7
- 8. Слайд 8
- 9. Если теперь сделать внутреннюю поверхность параболоида зеркальной
- 10. В обучении должна быть выделена система компонентов
- 11. Методика изучения темы «Квадратичной функции" Появление вычислительной
- 12. Применения компьютерных технологий при изучении квадратичной функции
- 13. Слайд 13
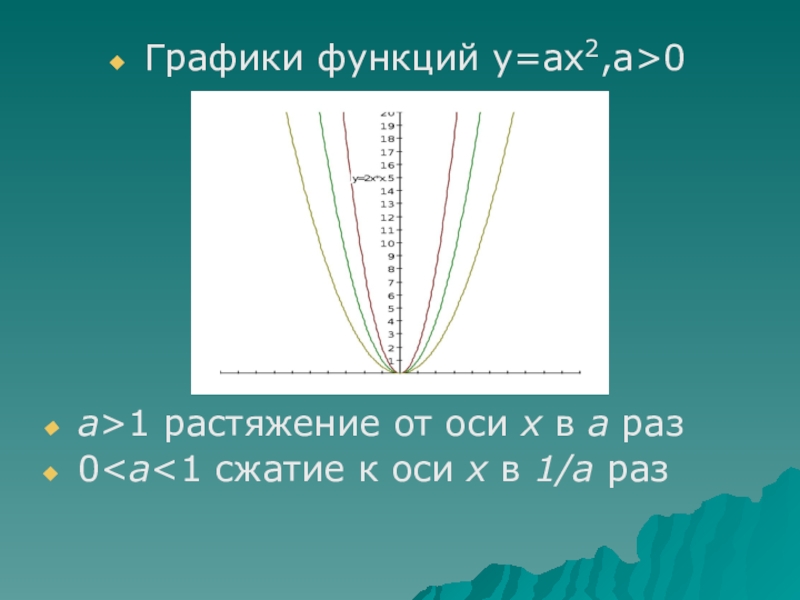
- 14. Графики функций у=ax2,а>0а>1 растяжение от оси х в а раз0
- 15. Слайд 15
- 16. Свойства функции при а
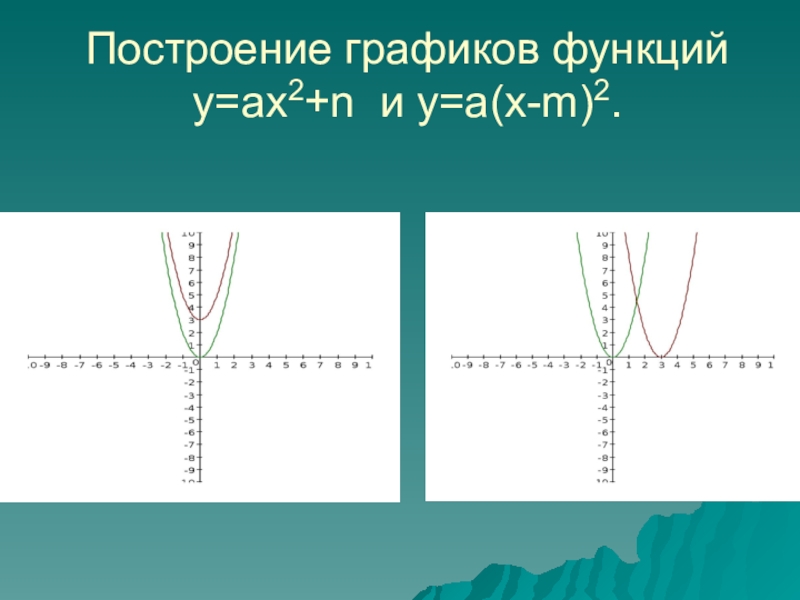
- 17. Построение графиков функций y=ax2+n и y=a(x-m)2.
- 18. Квадратичная функция и ее график. Квадратичной функцией
- 19. Пример построения графика квадратичной функции. F(x)= 2x²
- 20. На уроках - решения задач необходимо учесть
- 21. Задания для промежуточной проверки Первой группе дается
- 22. Заключение Использование компьютерной техники открывает огромные возможности
использование компьютерных технологий:- для построения графиков - для объяснения нового материаладля тестирования и самопроверки для проведения самостоятельных и контрольных работ Практическая направленность работы :
Слайд 1
Тема: Использование ИКТ при изучении квадратичной функции
Выполнил:
учитель математики
Стрижов О.В.
Слайд 2использование компьютерных технологий:
- для построения графиков
- для объяснения нового материала
для
тестирования и самопроверки
для проведения самостоятельных и контрольных работ
для проведения самостоятельных и контрольных работ
Практическая направленность работы :
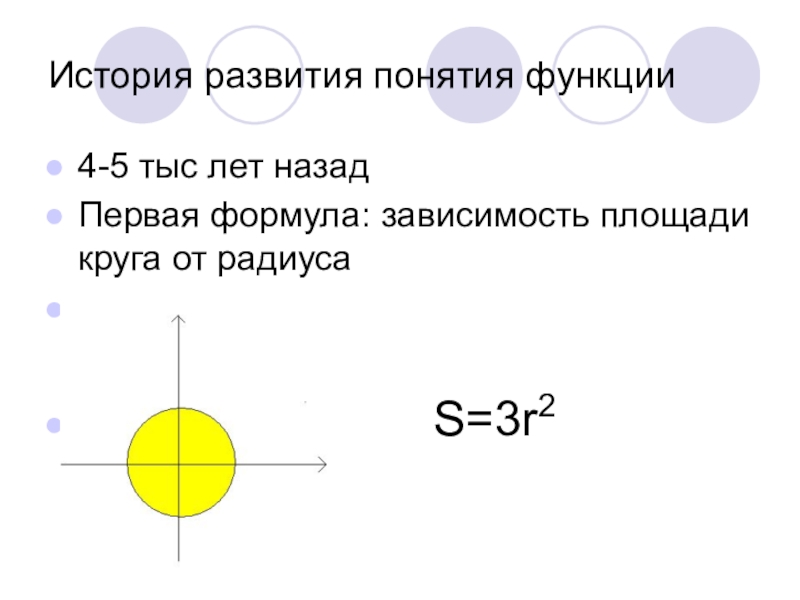
Слайд 3История развития понятия функции
4-5 тыс лет назад
Первая формула: зависимость площади
круга от радиуса
S=3r2
S=3r2
Слайд 4 17 век французские ученые Франсуа Виет и Рене Декарт разработали
единую буквенную математическую символику, обозначение: неизвестных —x, y, z,
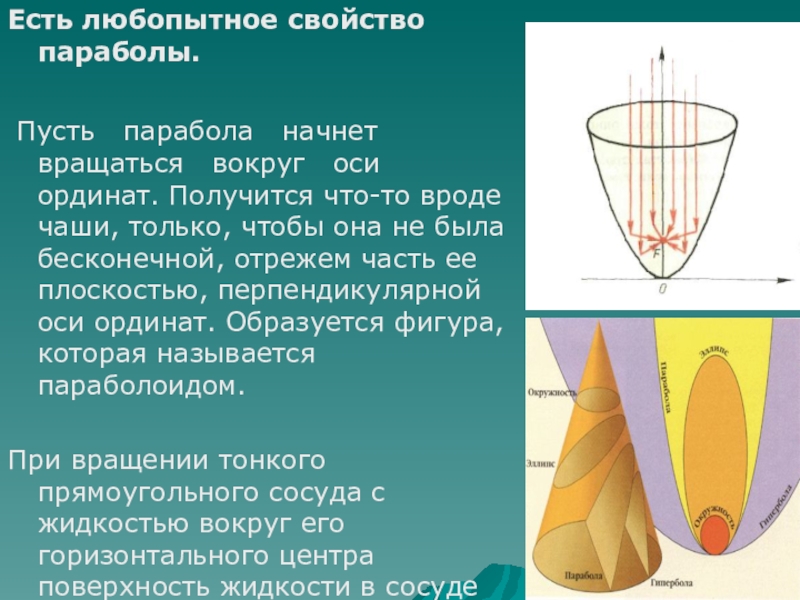
Слайд 6Есть любопытное свойство параболы.
Пусть парабола начнет вращаться
вокруг оси ординат. Получится что-то вроде чаши, только, чтобы она не была бесконечной, отрежем часть ее плоскостью, перпендикулярной оси ординат. Образуется фигура, которая называется параболоидом.
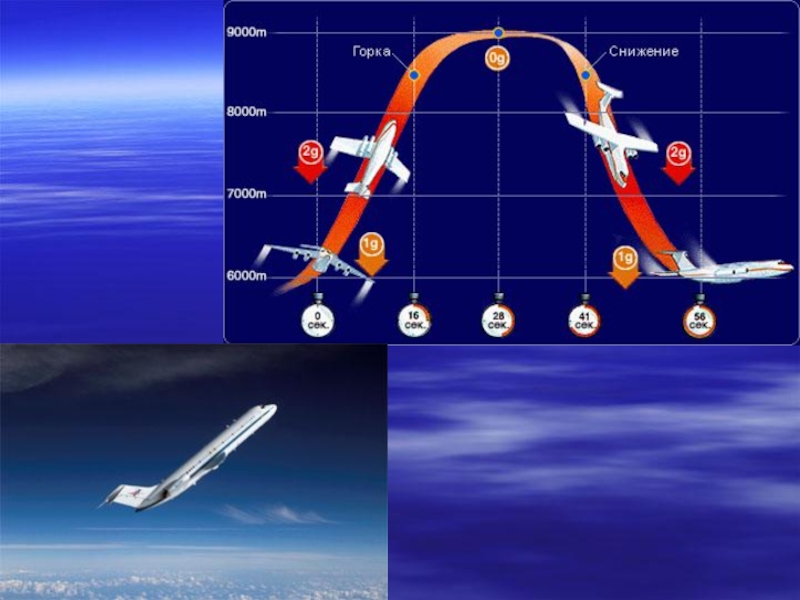
При вращении тонкого прямоугольного сосуда с жидкостью вокруг его горизонтального центра поверхность жидкости в сосуде принимает форму параболы
При вращении тонкого прямоугольного сосуда с жидкостью вокруг его горизонтального центра поверхность жидкости в сосуде принимает форму параболы
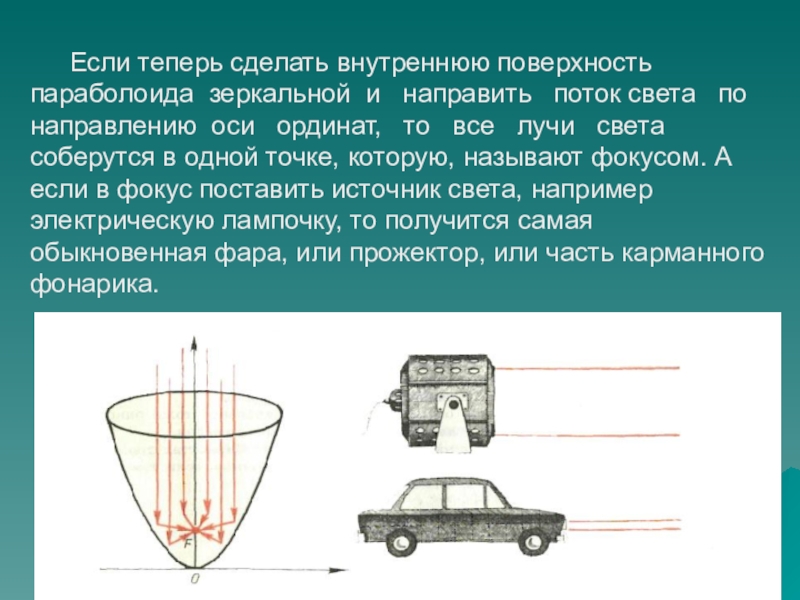
Слайд 9 Если теперь сделать внутреннюю поверхность параболоида зеркальной и направить
поток света по направлению оси ординат, то все лучи света соберутся в одной точке, которую, называют фокусом. А если в фокус поставить источник света, например электрическую лампочку, то получится самая обыкновенная фара, или прожектор, или часть карманного фонарика.
Слайд 10В обучении должна быть выделена система компонентов понятия функции и установлена
связь между ними. В эту систему входят такие компоненты:
представление о функциональной зависимости переменных величин в реальных процессах и в математике;
построение и использование графиков функций, исследование функций;
вычисление значений функций, определенных различными способами.
Слайд 11Методика изучения темы «Квадратичной функции"
Появление вычислительной техники в школе открыло возможности,
которые связаны с интеграцией новых информационных технологий в учебный процесс по различным школьным предметам.
Учитывая все преимущества компьютерных технологий, можно использовать ЭВМ на различных этапах учебной деятельности.
Учитывая все преимущества компьютерных технологий, можно использовать ЭВМ на различных этапах учебной деятельности.
Слайд 12Применения компьютерных технологий при изучении квадратичной функции в 9 классе.
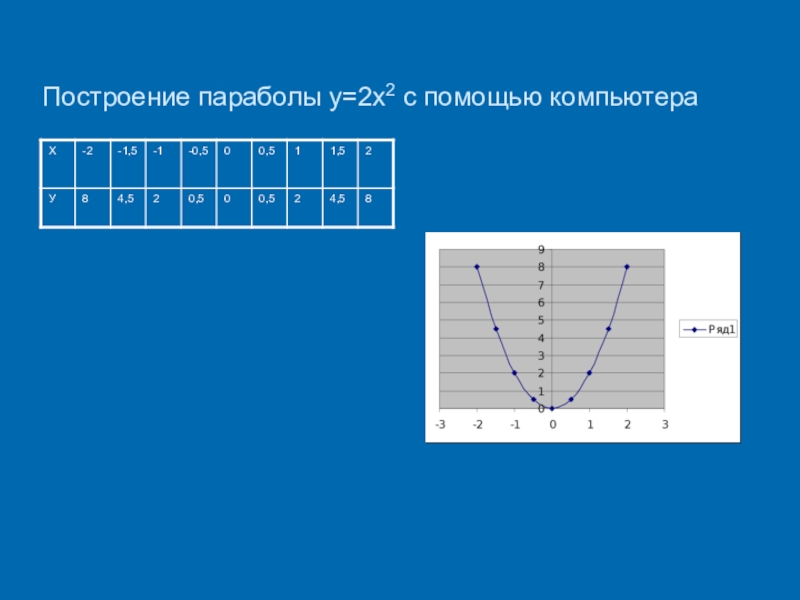
Изучение
темы начинаю с построения графика функции у=ах2 на множестве рациональных чисел. Для этого заполняется таблица значений функции х2 с шагом 0.5, на промежутке [-2;2]. Чтобы упростить вычисления, использую электронные таблицы.
Построение графиков провожу также в электронных таблицах.
Наблюдая, как изменяется положение точек при построении графиков, учащиеся делают предположение о существовании непрерывной функции на множестве R, графиком которой можно считать плавную кривую, соединяющую эти точки.
Построение графиков провожу также в электронных таблицах.
Наблюдая, как изменяется положение точек при построении графиков, учащиеся делают предположение о существовании непрерывной функции на множестве R, графиком которой можно считать плавную кривую, соединяющую эти точки.
Слайд 16Свойства функции при а
0, то у<0.
3. f(x)=f(-x).
4. Возрастает в
промежутке(- ;о].
5. Mах=0 при х=0.
Наименьшего
значения не имеет.
3. f(x)=f(-x).
4. Возрастает в
промежутке(- ;о].
5. Mах=0 при х=0.
Наименьшего
значения не имеет.
Слайд 18Квадратичная функция и ее график.
Квадратичной функцией называется функция, которую можно
задать формулой вида y = ax² + bx + c, где х – независимая переменная, a,b,c -некоторые числа, причём a ≠ 0.
Графиком квадратичной функции является парабола
Алгоритм построения параболы.
f(x) = ax² + bx + c
Направление ветвей
Вершина ( m = -b ∕ 2a; n = f(m ). )
Ось симметрии.
Таблица значений
Построение графика
Графиком квадратичной функции является парабола
Алгоритм построения параболы.
f(x) = ax² + bx + c
Направление ветвей
Вершина ( m = -b ∕ 2a; n = f(m ). )
Ось симметрии.
Таблица значений
Построение графика
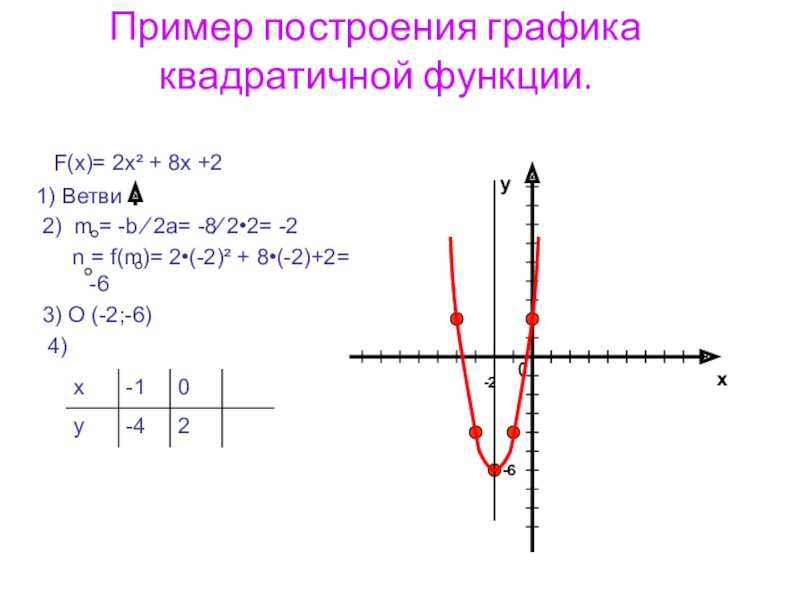
Слайд 19Пример построения графика квадратичной функции.
F(x)= 2x² + 8x +2
1) Ветви
2) m = -b ∕ 2a= -8∕ 2•2= -2
n = f(m)= 2•(-2)² + 8•(-2)+2= -6
3) O (-2;-6)
4)
у
х
-2
-6
Слайд 20На уроках - решения задач необходимо учесть неоднородность классного коллектива. Для
этого надо организовать работу так, чтобы каждый учащийся смог принять участие в решении. Но проверить на уроке все решения учителю не хватает времени. В этом помогает компьютер.
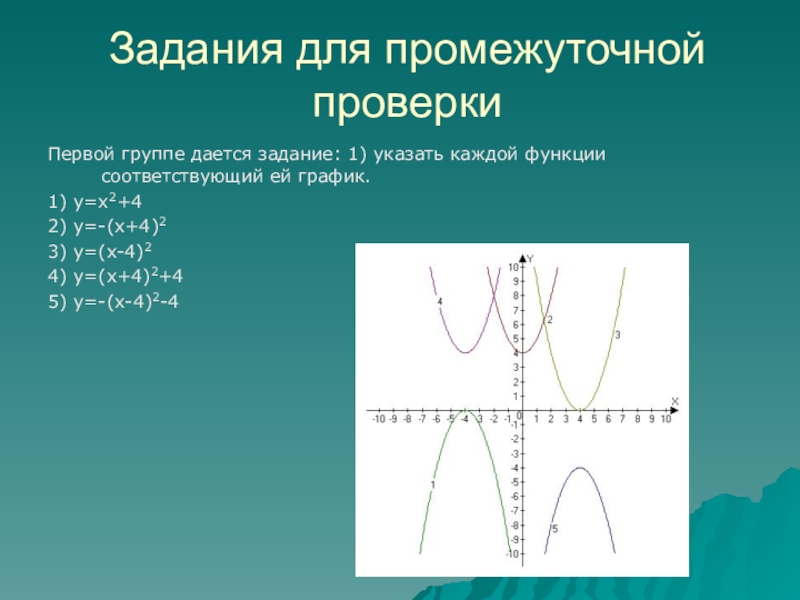
Слайд 21Задания для промежуточной проверки
Первой группе дается задание: 1) указать каждой
функции соответствующий ей график.
1) y=x2+4
2) y=-(x+4)2
3) y=(x-4)2
4) y=(x+4)2+4
5) y=-(x-4)2-4
1) y=x2+4
2) y=-(x+4)2
3) y=(x-4)2
4) y=(x+4)2+4
5) y=-(x-4)2-4
Слайд 22Заключение
Использование компьютерной техники открывает огромные возможности для педагога: компьютер
может взять на себя функцию контроля знаний, поможет сэкономить время на уроке, богато иллюстрировать материал, трудные для понимания моменты показать в динамике, повторить то, что вызвало затруднения, дифференцировать урок в соответствии с индивидуальными особенностями учащихся.
Использование компьютерных технологий на уроке позволяет:
· активизировать познавательную деятельность учащихся;
· обеспечить высокую степень дифференциации обучения (почти индивидуализацию);
· повысить объем выполняемой работы на уроке;
· усовершенствовать контроль знаний;
· формировать навыки подлинно исследовательской деятельности;
· обеспечить доступ к различным справочным системам, электронным библиотекам, другим информационным ресурсам.
Использование компьютерных технологий на уроке позволяет:
· активизировать познавательную деятельность учащихся;
· обеспечить высокую степень дифференциации обучения (почти индивидуализацию);
· повысить объем выполняемой работы на уроке;
· усовершенствовать контроль знаний;
· формировать навыки подлинно исследовательской деятельности;
· обеспечить доступ к различным справочным системам, электронным библиотекам, другим информационным ресурсам.